428

Результаты расчетов показали возможность использования процедуры линеаризации при решении краевых задач с большими деформациями. Процедура линеаризации позволяет конструировать алгоритм численного решения краевой задачи механики, включающей линеаризованные определяющие соотношения как многошаговый процесс с линейными физическими соотношениями на каждом шаге, поэтому можно ввести в рассмотрение температурные деформации и деформации структурной усадки известным образом: ввиде суперпозиции на каждом шаге тензора малых

деформаций e* , тензоров температурных и усадочных деформаций (последняявозникаеттольковкристаллическойфазематериала).

Библиографический список

1.Simulation of thermomechanical processen in crystallising polymer / I.N. Shardakov [et al.] // Polym. Engng and Sci. – 1997. – Vol. 37, No. 8. – P. 1270–1279.

2.Шардаков И.Н., Голотина Л.А. Моделирование деформационных процессов в аморфно-кристаллических полимерах // Вычислительная механика сплошных сред. – 2009. – Т. 2, № 3. – С. 106–113.

3.Завьялова Т.Г., Труфанов Н.А. Определяющие соотношения для вязкоупругого тела в условиях кристаллизации // Прикладная механика и техническая физика. – 2005. – Т. 46, № 4. – С. 78–87.

4.Новокшанов Р.С., Роговой А.А. Эволюционные определяющие соотношения для конечных вязкоупругих деформаций // Изв. РАН. Механика твердого тела. – 2005. – № 4. – С. 122–140.

5.Новокшанов Р.С., Роговой А.А. О построении зволюционных определяющих соотношений для конечных деформаций // Изв. РАН. Механика твердого тела. – 2002. – № 4. – С. 77–94.

6.Куликова Т.Г., Труфанов Н.А. Определяющие соотношения для кристаллизующегося полимерного материала и пошаговая процедура решения с учетом конечных деформаций // Вычислительная механика: сб. науч. тр. – Пермь: Изд-во Перм. гос. техн. ун-та, 2008. –

№ 7. – С. 170–180.

7.Методы прикладной вязкоупругости. / Адамов А.А. [и др.]; УрО РАН. – Екатеринбург, 2003. – 411 с.

8.Роговой А.А. Дифференцирование скалярных и тензорных функций тензорного аргумента // Вестник ПГТУ. Динамика и проч-

ность машин. – 2001. – № 2. – С. 83–90.

Получено 10.11.2010

71

УДК 532.2:519.7

М.Г. Бояршинов, Д.С. Балабанов

Пермский государственный технический университет

ПЕРЕНОС И РАССЕЯНИЕ ВОЗДУШНЫМ ПОТОКОМ ТЯЖЕЛОГО ГАЗА, ЭМИТИРОВАННОГО ТОЧЕЧНЫМ ИСТОЧНИКОМ

Для моделирования переноса и рассеяния выхлопных газов автомобильного транспорта используется система дифференциальные уравнения Эйлера (неразрывности, движения, энергии и состояния) в частных производных с соответствующими краевыми условиями. Численное решение поставленной задачи основано на методе крупных частиц (методе Давыдова). Учет плавучести отработанных газов ведется в рамках приближения Буссинеска.

Ключевые слова: газовая динамика, численные методы, приближение Буссинеска.

Возрастание интенсивности транспортных потоков приводит к росту объемов выбросов отработанных газов двигателей автомобильного транспорта. Для оценки уровня загрязнения атмосферного воздуха отработанными газами над территорией современного города требуется решить ряд связанных между собой задач.

В настоящей работе рассматривается задача о движении автомобиля, моделируемого как точечный источник, эмитирующий поток газа с интенсивностью m и мощностью ε, содержащий загрязняющую воздух пассивную газовую примесь ( q = 0,1m , то есть 10 % эмитируемой массы). Решение такой задачи обусловлено необходимостью исследования переноса и рассеяния отработанных газов от потока транспортных средств, моделируемого как множество отдельных подвижных точечных источников загрязняющей примеси различной интенсивности в произвольной пространственной области со сложной геометрией.

Использование численных методов в настоящее время является основным способом построения решений краевых задач газовой динамики. При исследовании подобных задач большее внимание уделяется конечно-разностным методам [1–4], требующим относительно малых вычислительных ресурсов. Значительный интерес вызывают схемы факторизации эволюционных дифференциальных уравнений [5, 6], по-

72

зволяющие «расщеплять» многомерные задачи на последовательности одномерных задач, что приводит к существенному повышению эффективности вычислительных алгоритмов. В ряде исследований [7–13] для решения задач движения сплошной среды используются методы конечных и граничных элементов с различными видами аппроксимации полей скорости, перемещения, плотности, давления, температуры и других характеристик.

Для решения прикладных задач механики сплошных сред интенсивно развивается и успешно применяется метод крупных частиц (метод Давыдова), позволяющий выполнять расчеты вихревых структур с учетом отрывных явлений, исследовать фильтрационные и струйные [14] течения, газо- и гидродинамические потоки с большими перемещениями и соударяющимися поверхностями раздела, движение многокомпонентных [15, 16], сыпучих и деформируемых сред [17], течения сквозь проницаемые объекты [18] и многие другие процессы. С использованием системы уравнений Эйлера построены трехмерные вычислительные модели взаимодействия струй с поперечными потоками [19, 20], истечения газа из отверстий и каналов [21, 22], воздействия ударных волн на препятствия и границы раздела сред [23, 24, 25], влияния локализованных источников энергии и массы на газодинамические характеристики газовых потоков [26, 27].

Для моделирования движения газовоздушной смеси используется система дифференциальных уравнений Эйлера (в дивергентной форме [17, 18, 29]), описывающая движение сплошной среды в рассматриваемой области, включающая эволюционные уравнения неразрывности

и концентрации (в рамках дифференциального приближения [28])

Здесь ρ – плотность газовоздушной смеси; V – вектор скорости потока с компонентами Vx , Vy , Vz ; U – полная удельная энергия; P – давле-

ние; С – концентрация загрязняющей примеси; k – показатель адиабаты; δ() – дельта-функция Дирака; rS – радиус-вектор положения то-

чечного источника; λ – коэффициент диффузии; q – интенсивность выброса смеси отработанных газов; qCO2 – интенсивность выброса диоксида углерода; Vq – скорость выброса смеси отработанных газов из

выхлопной трубы.

Точечный источник с координатами xS , yS , zS моделирует поло-

жение отверстия выхлопной трубы автомобиля в расчетной области G

(рис. 1).

Рис. 1. Схема расчетной области и обозначения ее границ

В начальный момент времени в области G известны распределения компонент вектора скорости, плотности, энергии, концентрации и давления:

Vx (0, x, y, z)=V0 , Vy (0, x, y, z)= 0 , Vz (0, x, y, z)= 0 , C (0, x, y, z)= 0 ,

ρ(0, x, y, z)= ρ0 , U (0, x, y, z)=U0 , P (0, x, y, z)= P0 x, y, z G .

Граничные условия имеют следующий вид:

74

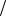Vx = 0 ,Vy = 0 ,Vz = 0 , ∂ρ∂z = 0 , ∂U∂z = 0 , ∂C∂z = 0 , x, y, z ∂G1 ;

∂Vx 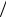∂z = 0 , ∂Vy 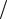∂z = 0 , ∂Vz 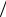∂z = 0 , ∂ρ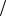∂z = 0 , ∂U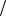∂z = 0 ,

ется приближение Буссинеска [0], согласно которому в предположении о малости концентрации C используется представление плотности газовоздушной смеси в виде

ности; начальная концентрация загрязняющей примеси отсутствует, то есть C0 = 0 .

Пусть в некотором объеме Ω содержатся воздух, имеющий плотность ρ0 , и пассивная газовая примесь с плотностью ρп , занимающая

где С – концентрация примеси в объеме Ω. Сравнение полученного выражения и соотношения (7) позволяет определить величину концентрационного коэффициента плотности:

75

α=1− ρ0 .

ρП

Для корректного учета скоростных граничных условий целесообразно полное давление газо-воздушной смеси Р в уравнениях (2)–(4) представить в виде суммы гидростатического давления Pг и отклонения p давления от гидростатического,

причем Pг = P0 −ρgz , P0 – давление воздуха на уровне поверхности

земли; g – ускорение свободного падения.

С учетом приближения выражений (7) и (8) уравнения движения (2), полной удельной энергии (3) и состояния (4) принимают вид

В соответствии с идеей метода крупных частиц система уравнений (1), (5), (9)–(11) расщепляется по физическим процессам. Расчет каждого временного слоя разбивается на три этапа. Для реализации первого (эйлерова) этапа считается, что изменяются лишь величины, относящиеся к ячейке в целом, а сплошная среда предполагается заторможенной. Система уравнений (1), (3), (5) и (11) представляется в виде

Уравнения этой системы записываются в виде явных конечноразностных схем:

76

V%xijk =Vxijk −(pi+1/2 jk − pi−1/2 jk )∆t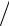ρijk hx ,

V%yijk =Vyijk −(pij+1/2k − pij−1/2k )∆t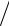ρijk hy ,

V%zijk =Vzijk −(pijk +1/2 − pijk −1/2 )∆t ρijk hz −αCijk g∆t ρijk ,

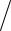U%ijk =Uijk −∆t {(pVx )i+1/2 jk −(pVx )i−1/2 jk hx + (pVy )ij+1/2k −(pVy )ij−1/2k hy +

+(pVz )ijk +1/2 −(pVz )ijk −1/2 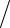hz + (PГVx )i+1/2 jk −(PГVx )i−1/2 jk 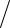hx +

+(PГVy )ij+1/2k −(PГVy )ij−1/2k 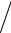hy + (PГVz )ijk +1/2 −(PГVz )ijk −1/2 hz }ρijk .

Вприведенных соотношениях величины с дробными индексами определяются как

Λi±1/2 jk ≡ (Λijk + Λi±1 jk ) 2 , Λij±1/2k ≡ (Λijk + Λij±1k ) 2 ,

Λijk ±1/2 ≡ (Λijk + Λijk ±1 )2 ,

где Λ принимает значения p, pVx , pVy , pVz PгVx , PгVy , PгVz .

На втором (лагранжевом) этапе вычисляются эффекты переноса, учитывающие обмен между ячейками при их перестройке на прежнюю эйлерову сетку. Определяются потоки массы за время ∆t через границы эйлеровых ячеек. Для учета направления движения сплошной среды потоки массы, импульса и полной удельной энергии определяются выражениями

77

В этих выражениях Λ принимает значения ρ, ρV%x , ρV%y , ρV%z , ρU% ,

C, CV%x , CV%y , CV%z .

На третьем, заключительном, этапе окончательные значения массы, импульса и энергии в момент времени tˆ = t + ∆t определяются законами сохранения массы, импульса и энергии, записанными с учетом промежуточных значений параметров потока:

Разностная аппроксимация уравнений приводит к системе разрешающих соотношений

78

По окончании третьего этапа в ячейке, где расположен точечный источник, в соответствии с уравнениями (1), (5) и (10) пересчитываются значения плотности, энергии и концентрации с учетом заданных величин q , qCO2 и Vq:

С использованием описанного алгоритма разработан комплекс программ для численного исследования пространственного переноса и рассеяния примесей, выбрасываемых точечным источником. Тестирование программного комплекса выполнено с использованием точного решения частной задачи об эмиссии сжимаемого газа точечным источником [31].

Для выполнения вычислительных экспериментов принято: интенсивность источника отработанных газов q = 1,2 г/с; интенсивность эмиссии диоксида углерода qCO2 = 0,12 г/с; скорость Vq = 10 м/с; пока-

затель адиабаты k = 1,67; плотность воздуха ρ0 = 1,29 кг/м3, плотность диоксида углерода (содержание в отработанных газах автотранспорта достигает 10 %, [0]) ρп = 1,98 кг/м3. Вычислительный эксперимент выполнялся с учетом ветра, изменяющегося по высоте рассматриваемой области линейно от 0 до 1 м/с (см. рис. 1).

80