
428
.pdfFa = |
µ1 eijeij + |
µ2 |
(eij |
−eij* )(eij −eij* )+ |
k1 |
ε2kk + |
|||
|
|||||||||
|
k2 |
|
2 |
2 |
|
2 |
|
||
+ |
|
(εkk −εkk )2 −(k1 +k2 )αT (T −T0 )εkk , |
|||||||
|
|||||||||
2 |
|
|
|
|
|
|
|
||
где µ1, k1 – сдвиговой и объемный модули, характеризующие упругие свойства полимера в высокоэластическом состоянии; µ2, k2 – сдвиговой и объемный модули, характеризующие упругие свойства, обусловленные межмолекулярным взаимодействием полимерной сетки; eij – компоненты девиатора тензора деформации; εkk – относительная объ-
емная деформация; eij , εkk – соответствующие тензорные величины,
которые на феноменологическом уровне характеризуют эволюцию межмолекулярного взаимодействия; T0 – температура окружающей среды; αT – коэффициент линейного температурного расширения аморфной фазы.
Для тензорных величинeij , εkk были сформулированы кинетические уравнения в аррениусовской форме:
|
|
|
Ua − |
µ |
|
|
* |
|
* |
|
|
|
||||
|
|
|
|
|
2 |
(eij −eij |
)(eij −eij |
) |
* |
|||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
& |
= Aa |
|
|
|
|
|
|
|
|
|
|
|
|
|
(eij −eij ), |
|
exp − |
|
|
|
|
|
|
|
|
|
|||||||
eij |
|
|
|
|
Tk (T ) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|||
|
|
|
|
Ub − |
|
|
(εkk −εkk ) |
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
||||||||||
& |
|
|
|
|
|
|
|
|
|
|
|
|
(εkk −εkk ), |
|
||
|
exp |
− |
|
|
|
|
|
|
|
|
||||||
εkk = Ab |
|
|
|
Tk (T ) |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Ua, Ub – величины, характеризующие энергию активации сегментарной подвижности полимерной сетки за счет физических связей межмолекулярного взаимодействия; Tk(T) – энергетическая температура; Aa, Ab – экспоненциальные сомножители, характеризующие величину, обратно пропорциональную характерному времени перехода межмолекулярных связей в равновесное состояние.
Путем численных экспериментов было установлено, что предложенная система определяющих и кинетических уравнений описывает характерные особенности термомеханического поведения аморфных полимеров. Для некоторого модельного аморфного полимерного материала рассмотрены однородные напряженно-деформированные состояния для нескольких историй силового и кинематического нагружения в температурном диапазоне, включающем интервал стеклования.
51
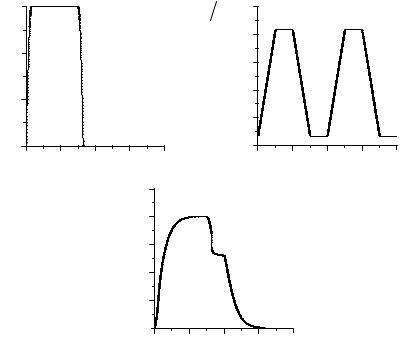
На рис. 1 представлены результаты численного эксперимента по моделированию эффекта памяти формы. Результаты представлены в относительных величинах.
σ 0,03. |
|
|
|
|
T Tg |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1,6. |
|
|
|
|
0,02. |
|
|
|
|
|
1,2 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
0,01 |
|
|
|
|
|
0,8. |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
0 |
|
|
|
|
t , мин |
0 |
|
|
|
160 t , мин |
0 |
40 |
t |
80 |
120 160 |
0 |
40 t |
80 t |
120 |
||
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
1 |
ε |
|
|
|
|
|
|
|
|
|
|
0,025 |
|
|
|
|
|
|
|
|
|
|
|
.025 |
|
|
|
|
|
|
|
|
|
|
0,02. |
|
|
|
|
|
|
0,15.015
0,01.
0,005.
0 |
40 t |
80 t |
|
160 t , мин |
0 |
0 |
|||
0 |
120 |
|
||
|
1 |
|
2 |
|
Рис. 1. Результаты численного эксперимента по моделированию эффекта памяти формы
Начальное недеформированное состояние образца – это состояние 1. Силовое нагружение образца производилось при температуре ниже температуры стеклования (T/Tg<1) до значения σx = 0,3 и выдерживалось постоянным до момента времени t = t1. При этом температура сначала повышалась до значения T >Tg, а затем снижалась до первоначального значения. В момент времени t = t1 силовая нагрузка снималась, но в образце появлялись остаточные деформации. Это – состояние 2. C момента времени t = t2 задается новый цикл изменения температуры до T >Tg и обратно. Образец возвращается в исходное состояние 1.
52
σ 0,05. |
|
|
|
|
ε |
0,02. |
|
|
|
|
0,04. |
|
|
|
|
|
0,016.016 |
|
|
|
|
0,03. |
|
|
|
|
|
0,012. |
|
|
|
|
0,02. |
|
|
|
|
|
0,008. |
|
|
|
|
0,01. |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
0,004 |
|
|
|
|
|
0 |
10 |
20 |
|
30 t , мин |
0 |
0 |
10 |
20 |
t , мин |
|
0 |
|
30 |
|
|
30 |
|||||
|
|
а |
|
|
|
|
|
|
б |
|
|
|
σ |
. |
|
|
|
|
|
|
|
|
|
0,05 |
|
|
|
|
|
|
|
|
|
|
|
0,04. |
|
|
|
|
|
|
|
|
|
|
0,03. |
|
|
|
|
|
|
|
|
|
|
0,02. |
|
|
|
|
|
|
|
|
|
|
0,01. |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
. 4 |
. 8 |
. 12 |
. 16 . |
|
|
|
|
|
|
0,004 |
0,008 0,012 0,016 0,02 |
|
|
|
|||
|
|
|
|
|
в |
|
|
|
|
|
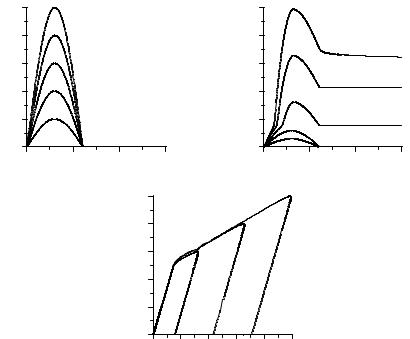
Рис. 2. Результаты численного моделирования силового изотермического |
||||||||||
деформирования при температуре ниже температуры стеклования: |
||||||||||
а– графики изменения заданного значения напряжения; б – графики отклика;
в– графики изменения заданного значения напряжения от деформации
Результаты численного моделирования силового изотермического деформирования при температуре ниже температуры стеклования приведены на рис. 2. На рис. 2, а представлены графики изменения заданного значения напряжения, а на рис. 2, б – графики отклика (деформации εx) на соответствующее силовое воздействие. Результаты демонстрируют появление эффектов вынужденной высокоэластичности и обратной ползучести. При низких значениях максимальных напряжений материал ведет себя упруго. При определенном уровне максимальных напряжений материал проявляет повышенную деформируемость, в образце появляются остаточные деформации, а при дальнейшем увеличении максимальных напряжений в разгруженном образце наблюдается эффект обратной ползучести – уменьшение величины остаточных деформаций во времени.
53
Проведенные численные эксперименты позволили разработать программы экспериментального исследования термомеханического поведения аморфного полимера (ПММА) для определения материальных констант, входящих в определяющие и кинетические уравнения. Для определения модулей µ1 и µ2 а также энергии активации предлагается использовать результаты испытания образцов на установке DMA 242. Для определения остальных констант предлагается использовать результаты исследования при различных программах температурновременного нагружения на универсальной испытательной машине Zwik.
Библиографический список
1.Varghese A.G., Batra R.C. Constitutive equations for thermomechanical deformations of glassy polymers // Internation J. of Solids and Structures. – 46 (2009). – 4079–4094.
2.Wool R.P. Tvinkling fractal theory of the glass transition // J. of Polymer Sci. Part B: Polymer Phisics. – 46 (2008). – 2765–2778.
3.A thermo-mechanically coupled large-deformation theory for amorphouse polymers in a range which spans their glass transition / Vikas Srivastava [et al.] // Int. J. of Plasticity. – 26 (2010). – 1138–1182.
4.A new strain path to inducing phase transition in semi-crystalline polymers / E.N. Brown [et al.] // Polymer. – 48 (2007). – 2531–2536.
5.Thermomechanics of shape memory polymers: uniaxial experiments and constitutive modeling / Yipin Lui [et al.] // Int. J. of Plasticity. – 22 (2006). – 279–313.
6.Термомеханика полимерных материалов в условиях релаксационного перехода / В.П. Матвеенко [и др.]. – М.: Физматлит, 2009. – 176 с.
7.Слуцкер А.И., Поликарпов Ю.И., Васильева К.В. Определение энергии активации сложных релаксационных процессов // Физика твердого тела. – 2002. – Т. 44, вып. 2. – С. 1529–1555.
Получено 10.11.2010
54
УДК 539.376
Т.Г. Куликова
Пермский государственный технический университет
К ОПИСАНИЮ ДЕФОРМИРОВАНИЯ КРИСТАЛЛИЗУЮЩЕГОСЯ ПОЛИМЕРНОГО МАТЕРИАЛА С УЧЕТОМ БОЛЬШИХ ДЕФОРМАЦИЙ
Предлагаются определяющие соотношения для кристаллизующегося упругого материала с учетом конечных деформаций. Рассматривается процедура линеаризации при решении краевых задач с большими деформациями, позволяющая ввести в рассмотрение температурные деформации и деформации структурной усадки материала. Работоспособность модели тестируется на задачах простого сдвига и одноосного деформирования.
Ключевые слова: кристаллизация, конечные деформации, линеаризация.
Технологический процесс по производству значительной части полимерных изделий и конструкций содержит этап охлаждения материала, сопровождающийся его кристаллизацией. Технологические и остаточные напряжения, формирующиеся в таких изделиях вследствие температурной и деформационной неоднородностей, могут приводить к снижению эксплуатационных качеств изделий и даже их разрушению еще на стадии изготовления. Поэтому актуальной становится проблема описания термомеханических процессов в полимерных материалах в условиях фазового перехода. Учитывая, что многие полимеры претерпевают существенную структурную усадку, связанную с переходом из одного фазового состояния в другое, определяющие соотношения для описания таких термомеханических процессов, по возможности, должны быть построены для случая больших деформаций.
Построению определяющих соотношений для кристаллизующихся сред посвящено достаточно большое количество работ. Ряд из них рассматривают кристаллизующуюся среду в каждой точке как двухкомпонентную смесь аморфной фазы и полностью закристаллизовавшегося продукта [1–3], не выделяя фронт кристаллизации, что характерно для большинства кристаллизующихся полимерных материалов. К настоящему времени предложены определяющие соотношения для кристаллизующейся среды, построенные для случая малых дефор-
55
маций с учетом [3] и без учета [1] вязкоупругих свойств материала. В работе [2] предложен вариант определяющих соотношений, которые описывают связь напряженно-деформированного состояния с процессами кристаллизации и стеклования, позволяют описать эффекты вынужденной высокоэластичности, но не учитывают конечных деформаций. Соотношения, которые приводятся в данной публикации, являются развитием соотношений, предложенных в работах [1, 3], на случай учета конечных деформаций материала. При построении соотношений учет конечных деформаций осуществлен по аналогии с подходами, изложенными в работах [4, 5], в которых соотношения получены на основе кинематики наложения малых деформаций на конечные деформации безотносительно процесса кристаллизации.
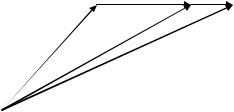
При получении определяющих соотношений с учетом конечных деформаций для кристаллизующегося материала использованы понятия начальной (соответствующей моменту времени t = 0) и текущей (соответствующей моменту времени t) конфигураций [5]. Наряду с текущей и начальной конфигурациями тела в рассмотрение введена некоторая промежуточная конфигурация (соответствующая моменту времени τ, 0 < τ < t). Начальная конфигурация определяется радиусвектором r = r(x, y, z) , текущая конфигурация – радиус-вектором
τ τ
R = R(x, y, z) , а промежуточная – радиус-вектором R = R(x, y, z) (рис. 1). В каждой из конфигураций введены в рассмотрение основные
и взаимные базисы: r , ri , R |
τ |
τ |
|
, Ri , Ri , |
Ri . |
||
i |
i |
|
|
uτ u
r |
τ |
R |
|
R |
|||
|
|
Рис. 1. Связь начальной, промежуточной и текущей конфигураций
При получении определяющих соотношений кристаллизующаяся из расплава система рассматривается как двухкомпонентная смесь исходного и конечного продуктов, доля которых в общем объеме определяется степенью кристаллизации полимера α(t ).
Упругий потенциал кристаллизующейся системы может быть представлен в виде суммы упругого потенциала для аморфной фазы иупругого потенциаладлякристаллическойфазыследующимобразом[6]:
56

W (G×t )= (1−α(t ))Wa (G×t )+Wкр1 +Wкр2 +...+Wкрn , |
(1) |
где Wкрi =Wкр (G×ti −t )∆αi – доля потенциала, которую привносит в об-
щий потенциал часть кристаллической фазы, соответствующая приращению степени кристаллизации ∆αi в момент времени ti ; G×t = FT F –
тензор меры деформаций Коши-Грина [5], соответствующий деформированию от начального до текущего момента времени; F – градиент места из начальной конфигурации в текущую конфигурацию;
G× |
−t |
= FT F |
– тензор меры деформаций Коши-Грина, соответствую- |
t |
i i |
|
|
i |
|
|
|
щий деформированию от момента времени ti до текущего момента вре-
мени; Fi – градиент места из конфигурации, в которой появилась доля кристаллической фазы ∆αi , в текущую конфигурацию; Wa (G×t ) – уп-
ругий потенциал аморфной фазы.
Учитывая, что G×ti −t = ft−i T G×t ft−i 1 [6], после осуществления пре-
дельного перехода в соотношении (1) по степени кристаллизации выражение для упругого потенциала можно записать в виде
W (G×t )= (1−α(t ))Wa (G×t )+ α∫(t )Wкр (fτ−T G×t fτ−1 )dα(τ),
0
где fτ – градиент места из начальной конфигурации в конфигурацию, соответствующую моменту времени τ.
Потенциал W (G×t ) позволяет получить определяющие соотно-
шения в виде
Q = J −1PII ,
где |
Q = tijr r |
j |
– энергетический тензор напряжений; J = G / g ; |
|
i |
|
G = det (Gij ) – определитель матрицы ковариантных компонент метри-
ческого тензора в текущей конфигурации; g = det (gij ) – определитель матрицы ковариантных компонент метрического тензора в начальной конфигурации g ; PII = 2∂W (G×t )/ ∂G×t – тензор Пиола–Кирхгофа 2-го рода.
57

В работе [7] рекомендуется в качестве упругого потенциала для полимерных материалов вариант двухконстантного потенциала Пенга– Ландела
W= 12 µ(I1I3−1/3 −3) + 12 B(I31/2 −1)2 .
Вэтом случае, суммируя напряжения от аморфной и кристалли-
ческой фаз ( Qa = 2J −1∂Wa (G×t )/ ∂G×t и Qкр = 2J −1∂Wкр (G×t )/ ∂G×t ,
Wкр (G×t )= α∫(t )Wкр (fτ−T G×t fτ−1 )dα(τ)), с учетом правил дифференци-
0
рования тензорных функций [8], получаем определяющие соотношения в виде
|
|
|
|
|
−5/6 |
I1 |
× |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
(Gt |
|
|
|
|
|
|
|
||||||
Q(t )= µa (I3 (G×t |
)) |
|
g − |
|
|
|
G×−t |
1 + Ba (θ(G×t |
)G×−t |
1 ) |
(1 |
−α(t)) + |
|||||
|
|
3 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α(t) |
|
|
|
|
−5/6 |
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 (Gτ−t ) |
|
|
|
|
|
|
||||||
+ ∫ |
µкр |
(I3 |
(G×τ−t )) |
g − |
|
|
|
|
G×τ−t−1 + Bкр (θ(G×τ−t )G×τ−t |
−1 ) dα(τ) + |
|||||||
|
3 |
|
|
||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α(t)
+∫
0
|
|
|
|
|
|
I1 |
× |
|
|
|
|
|
|
|
|
|
|
I3 (G×τ ) |
) |
−5/6 |
(Gτ ) |
|
|
|
( |
θ(G×τ )G×−τ |
|
) |
|
||||
µа |
|
g − |
|
|
G×−τ |
1 |
|
+ Bа |
1 |
dα(τ), (2) |
||||||
|
|
3 |
|
|
||||||||||||
|
( |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где µa , Bа, Bкр,µкр – константы материала для аморфной и кристаллической фазы соответственно; θ – относительное изменение объема; I1, I2 , I3 – главные инварианты тензора второго ранга, определяемые
обычным образом [7]; (G×t )−1 – тензор, обратный к тензору меры де-
формаций Коши–Грина.
На практике часто используют процедуру линеаризации нелинейных соотношений для решения задач с большими упругими деформациями. Процедура линеаризации дает возможность конструировать алгоритм численного решения краевой задачи механики как многошаговый процесс с линейными физическими соотношениями на каждом шаге, что позволяет ввести в рассмотрение температурные деформации и деформации структурной усадки известным образом:
58
в виде суперпозиции на каждом шаге тензора малых деформаций, тензоров температурных и усадочных деформаций. Проиллюстрируем определяющие соотношения (2) и возможность их линеаризации на примере некоторых случаев простого деформирования в декартовой системе координат.
Простой сдвиг
Пусть вектор перемещений точек тела определен составляющими ux = sty , uy = 0 , uz = 0 ,
где ui – компоненты вектора перемещений, s – скалярная величина, t – время, x, y, z – декартовы координаты.
Радиус-векторы произвольной точки тела в начальной и текущей конфигурации имеют вид
r = xi + yj+ zk ,
R = (sty + x)i + yj+ zk ,
где i, j,k – базисные векторы декартовой системы координат. Базисные векторы основных базисов начальной и текущей кон-
фигураций определяются следующим образом: r1 = i , r2 = j, r3 = k ;
R1 = i, R2 = sti + j, R3 = k .
Базис Ri определяет ковариантные компоненты метрического тензора в текущей конфигурации:
|
1 |
st |
0 |
|
|
|
||
G |
= st |
s2t2 +1 |
0 |
|
, |
G = det(G |
) =1. |
|
ij |
|
0 |
0 |
|
|
|
ij |
|
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
Контравариантные компоненты метрического тензора в текущей конфигурации, полученные по ковариантным компонентам, позволяют определить взаимный базис текущей конфигурации:
R1 = i − stj, R2 = j, R3 = k .
Взаимный базис начальной конфигурации совпадает с основным. Основной и взаимный базисы текущей конфигурации позволяют определить операторы Гамильтона относительно начальной и проме-
59
жуточной конфигураций в базисе начальной системы координат, применительно к вектору перемещений произвольной точки u относительно соответствующей конфигурации:
|
|
0 |
0 |
|
|
u = st |
0 |
|
|
|
0 |
|
|
0 |
|
|
|
0 |
0 |
|
|
u = s(t −τ) 0 |
|
|
|||
|
|
|
0 |
|
|
0 |
|
0
0 , u = styi; (3)
0
0
0 , u = s(t −τ) yi.
0
Определим градиент места из начальной конфигурации в текущую, используя соотношение (3)
F = ( R)T = g +( u)T , |
(4) |
t |
|
где g – метрический тензор, определенный в начальной конфигурации, совпадающий с единичным тензором, g = det(gij ) =1.
Используя (4), получим тензор меры деформаций Коши-Грина, соответствующий деформированию тела от начального до текущего момента времени и обратный к нему тензор в базисе начальной конфигурации
|
|
1 |
st |
|
|
0 |
|
) |
−1 |
|
1 |
+ s2t2 |
− st |
0 |
|
|
|
× |
T |
Ft = st |
2 |
t |
2 |
0 |
|
× |
= |
|
− st |
1 |
0 |
|
.(5) |
||
Gt |
= Ft |
1+ s |
|
, (Gt |
|
|
|
||||||||||
|
|
0 |
0 |
|
|
1 |
|
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Инварианты G×t имеют вид
I (G×) = 3 + s2t2 |
, I |
(G×) =1, θ(G×) = 0, |
(6) |
||
1 |
t |
3 |
t |
t |
|
что отражает специфику деформирования и соответствует нулевому изменению объема.
Аналогично определим все величины, соответствующие деформированию тела от промежуточного момента времени τ до текущего момента времени t :
1
G×τ−t = s (t −τ)0
s (t −τ) |
0 |
|
|
1+ s2 (t −τ)2 |
0 |
, |
(7) |
0 |
1 |
|
|
|
|
|
|
60
