564

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Пермский государственный технический университет

И.Э. Келлер

ДИНАМИКА И ПРОЧНОСТЬ МАШИН

Методы возмущений

Утверждено Редакционно-издательским советом университета

в качестве учебного пособия

Издательство Пермского государственного технического университета

2008

УДК 517.94 К34

Рецензенты:

д-р физ.-мат. наук А.А. Роговой (Институт механики сплошных сред УрО РАН);

канд. физ.-мат. наук А.В. Зайцев (Пермский государственный технический университет)

Келлер, И.Э.

К34 Динамика и прочность машин. Методы возмущений: учеб. пособие / И.Э. Келлер. – Пермь: Изд-во Перм. гос. техн. ун-та, 2008. – 77 c.

ISBN 978-5-398-00079-5

Излагается метод многих масштабов асимптотического анализа, предназначенный для построения решений задач вблизи некоторого предельного состояния в виде равномерно сходящихся рядов. Содержащиеся в пособии примеры решения задач, относящихся к различным областям механики, способствуют быстрому практическому освоению этой важной области прикладной математики.

Адресовано студентам-механикам магистерской ступени обучения инженерных вузов и университетов.

УДК 517.94

Издано в рамках приоритетного национального проекта «Образование» по программе Пермского государственного технического университета «Создание инновационной системы формирования профессиональных компетенций кадров и центра инновационного развития региона на базе многопрофильного технического университета»

2

Кафедре «Динамика и прочность машин»

Пермского государственного

технического университета

к её 45-летию

3

4

ВВЕДЕНИЕ

Вразличных линейных и нелинейных задачах иногда возникает возможность значительного упрощения их постановки в окрестности некоторого предельного состояния. Для того чтобы строить вблизи этого состояния равномерно сходящиеся ряды, существуют специальные методы – методы возмущений. Данное небольшое учебное пособие, адресованное студентаммеханикам преимущественно магистерской ступени обучения инженерных вузов и университетов, предназначено для быстрого практического освоения этой важной области прикладной математики.

Впервых четырёх главах показано применение методов возмущений для решения простейших начальных или краевых задач на базе обыкновенных дифференциальных уравнений: рассмотрены осцилляторы со слабой вязкостью и слабой нелинейностью, системы с малыми параметрическими колебательными возмущениями и погранслоем. В остальной части учебного пособия рассматриваются процессы или состояния в сплошных средах (идеальной жидкости, нелинейно-вязкой, линейно-упругой и идеально-пластической средах). В главах 5 и 6 исследуются нелинейные задачи об уединенных волнах на свободной поверхности жидкости: солитоне Кортевега – де Фриза

игрупповом солитоне. В главе 7 исследуется нелинейная задача о растяжении «сверхпластической» полосы, имеющая солитоноподобные решения для эволюции свободной поверхности, являющиеся следствием баланса диссипативности и открытости данной системы. Глава 8 посвящена применению методов возмущений в задачах нахождения эффективных упругих свойств структурно-неоднородных сред. В главе 9 изучается структура поля напряжений в идеально-пластической среде с периодически изменяющимся по пространству пределом текучести.

Большинство глав содержат концептуальную и математическую постановки задач, процедуру выделения малых параметров, применение методов возмущений и получение аналитических решений. Из множества методов возмущений предпочтение отдано методу многих масштабов и одной его разновидности – редуктивной теории возмущений.

Задачи, рассмотренные в главах 1–4, заимствованы из учебника [1], в главе 5 – из монографии [9], в главе 6 – из монографии [10], в главе 8 – из монографии [14]. В главах 7 и 9 изложены результаты, полученные автором.

Пониманием многих относящихся к делу вопросов автор обязан профессорам Э.Л. Аэро (ИПМаш. РАН) и В.В. Киселёву (ИФМ УрО РАН), за что выражает им искреннюю благодарность.

5

1.ЗАДАЧА С МАЛЫМ ПАРАМЕТРОМ ПРИ СТАРШЕЙ ПРОИЗВОДНОЙ

Рассмотрим краевую задачу [1]

Подставим разложение (1.3) в уравнение (1.1) и граничные условия (1.2):

Приравнивая коэффициенты при линейно независимых степенях , получим:

и т.д. Общее решение уравнения для y0 имеет вид y0 Aexp( x)

и содержит одну произвольную постоянную. Это решение не может одновременно удовлетворять двум граничным условиям задачи (1.4). Если выбрать первое граничное условие, получим:

y0 exp( x) ,

а если второе, то

y0 exp(1 x) ;

и если только не равно e , задача (1.4) некорректна.

6

Таким образом, на первый взгляд разумная попытка искать решение задачи (1.1)–(1.2) в виде степенного ряда (1.3) по малому параметру этой задачи потерпела неудачу. Поэтому необходимо выяснить причины несостоятельности использования прямого разложения (1.3) и разработать методы, приводящие к успеху в решении подобных задач.

С этой целью попробуем сначала получить точное решение нашей задачи. Решение линейного дифференциального уравнения с постоянными коэффициентами ищем в виде

y Aexp( x) .

Получаем уравнение для :

2 (1 2 ) 1 2 0 ,

эквивалентное уравнению

( 1 )( 1 ) 0 ,

корни которого

7

yexp((1 )(1 x)) ( exp(1 )) exp( ( 1 1)x)

O(exp( 1 )). (1.6)

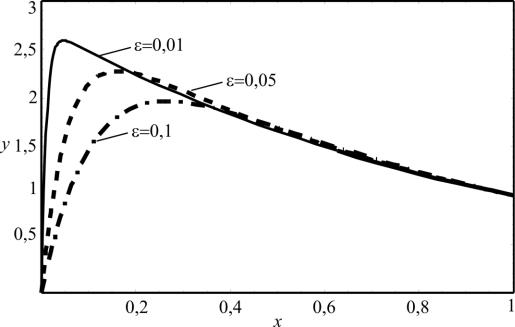
Вид решения (1.6), соответствующий 0 и 1 при 0,01; 0,05 и 0,1, представлен на рис. 1.1. Уравнение (1.1) имеет малый параметр при старшей производной и описывает погранслой, в данном случае вблизи левой границы. Теперь разложим решение (1.6) в степенной ряд по . Для этого требуется знать порядок множителя x по сравнению с во втором слагаемом этого выражения. Для значений x , больших , второе слагаемое экспоненциально мало по сравнению с первым и имеет место выражение

Таким образом, проблема заключается в том, что ряд (1.7) не обладает равномерной сходимостью для всех интересующих нас значений x [0;1] .

Рис. 1.1. Зависимость точного решения задачи от малого параметра

При разложении в ряд функции (1.6) фактически мы фиксировали x как параметр. С целью удержания в разложении второго слагаемого выражения (1.6) попытаемся зафиксировать входящий в него комплекс 1x . При этом будем иметь функцию

8

Это выражение уже принимает на левом конце правильное значение y(0) , но на правом – неправильное y(1) e . Более того, разложение (1.10) правильно ведет себя и вблизи левой границы, описывая погранслой.

Можно сделать вывод, что равномерно пригодное для любых x разложение нельзя получить, используя лишь один определенный масштаб по x , то есть определенную комбинацию x и . Эта идея лежит в основе метода многих масштабов, предлагающего считать искомые функции в разложении (1.3) зависящими от нескольких независимых переменных: ..., 2 x, 1x, x, x, 2 x, ... , –

сжатых или растянутых в масштабе n , где n – целое число. Обозначаяn x n , запишем представление решения обыкновенного дифференциального уравнения в виде

y(x, 1, 2 ,...) y0 (x, 1, 2 ,...) y1(x, 1, 2 ,...) 2 y2 (x, 1, 2 ,...) ...

Как мы показали выше, для нашей задачи достаточно кроме x рассматривать растянутую координату 1x . В таком случае решение представля-

Подставляя (1.11) и (1.12) в уравнение (1.1), получаем:

( y0 ,xx 2 1 y0 ,x 2 y0 , y1,xx 2 y1,x 1 y2 , ...)

(1 2 )( y0 ,x 1 y0 , y1,x y1, ...) (1 2 )( y0 y1 ...) 0.

9

Собирая коэффициенты при линейно независимых степенях , начиная со старшей 1 , и приравнивая их нулю, получаем рекуррентную последовательность дифференциальных уравнений:

следующим образом. Подставим решение (1.15) в правую часть (1.14), в результате чего получим уравнение

y1, y1, 2B,x exp( ) A,x B,x exp( ) A B exp( ) ,

приводимое к виду

Рассмотрим внимательно уравнение (1.16). Это уравнение относительно у1 имеет левую часть, идентичную уравнению (1.13) относительно у0 . Правая часть (1.16) также имеет структуру решения (1.15) уравнения (1.13). Такое совпадение структуры общего решения дифференциального уравнения и его правой части вызывает появление в частном решении вековых членов (в теории колебаний это называется резонансом). Действительно, частное решение (1.16) имеет вид

Для нашей процедуры появление вековых членов ведет к расходимости ряда (1.11). Действительно, вспоминая, что 1x , мы получаем:

y A(x) B(x)exp( ) x(C(x) D(x)exp( )) ,

то есть второй член ряда (как и все последующие) становится того же порядка, что и первый. В методе многих масштабов имеется свобода распорядиться произволом определения функций A(x) и B(x) таким образом, чтобы устранить резонанс в уравнении (1.16). Мы добьемся этого, полагая

10