564

(exp(2it) exp( 2it))(a exp(i t) a exp( i t))

или

и 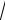1 1 , где 1 ~ O(1) . В первом из них для устранения вековых членов в частном решении (4.33) следует потребовать, чтобы a, 0 , и мы получаем колебательный режим:

a0 cos( 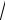t 0 ) O( ) . (4.34)

Обратимся к более интересному второму случаю. Мы получаем уравнение (2 )t t 2 1 и, учитывая, что разномасштабные временные переменные t и считаются независимыми, для устранения вековых членов должны требовать уже, чтобы

32

Переменная изменяется неограниченно (см. (4.37)), при этом cos изменяется в пределах от -1 до 1. Следовательно, при условии 1 2 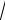1 1

имеем переход от неустойчивого движения к устойчивому. Поскольку у нас

1 1 , то 1 12 . Следовательно, в плоскости параметров , переходные кривые, выходящие из точки 0; 1, описываются уравнениями

что можно наблюдать на рис. 4.4.

Для получения зависимости ( ) нужно решить уравнение (4.38) с учетом (4.41). Опуская эту процедуру, приведем сразу выражение первого приближения в терминах t :

где константы i определяются начальными условиями.

33

5. УЕДИНЕННАЯ ВОЛНА НА ПОВЕРХНОСТИ ВОДЫ

Одними из интереснейших нелинейных объектов являются знакомые всем волны на поверхности воды. Мы рассмотрим два явления из этой серии – распространение уединенной волны и уединенной группы волн на воде. Редкий читатель не осведомлен об уединенной волне цунами, нелинейность которой позволяет ей преодолевать полтора десятка тысяч километров от места зарождения у тектонически-нестабильного побережья Чили до противоположных берегов Тихого океана. Выражение «девятый вал», не оставляющее равнодушными тех, кто в детстве зачитывался приключенческими романами, оказывается, также имеет под собой реальные основания. Это явление имеет нелинейное происхождение – большая группа волн на воде вследствие нестабильности распадается на небольшие группы волн. Методы возмущений здесь сыграли роль, важность которой трудно переоценить; в частности, они позволили на заре изучения нелинейных явлений в 1895 году Кортевегу и де Фризу получить знаменитое модельное нелинейное уравнение, описывающее распространение уединенных длинных пологих волн на мелководье, и проинтегрировать его. С этого классического примера мы и начнем.

Порекомендуем читателю, желающему более глубоко изучить волновую тематику, монографии [5,8,9].

Для построения по возможности простой математической модели интересующего нас явления придется наложить ряд упрощающих ограничений кинематического, статического и физического характера. Правомерность наложения тех или иных ограничений обычно проверяется опытом, апостериорно, поэтому их часто называют «гипотезами».

Итак, имеется слой жидкости с горизонтальным дном и свободной поверхностью. Проще рассматривать прямолинейную волну, для которой задача ставится в плоскости ее поперечного сечения. «Берега» такого плоского слоя мы будем считать бесконечно удаленными. На рис. 5.1 представлена схема рассматриваемой области, где x – горизонтальная координата, z – вертикальная, отсчитываемая от дна, h – высота слоя жидкости в невозму-

в исследуемой задаче.

Относительно жидкости принимаются гипотезы идеальности и несжимаемости. Принимается во внимание сила тяжести, ответственная за существование волн в данных условиях. Кроме того, будем считать движение

34

жидкости потенциальным. Последняя гипотеза оправдывается теоремой Лагранжа: движение первоначально покоящейся идеальной несжимаемой жидкости под действием потенциальных сил потенциально. Эта гипотеза типична при рассмотрении волновых процессов в идеальной жидкости.

Рис. 5.1. Схема уединенной волны на мелководье в декартовой системе координат

Потенциальность движения означает существование функции , с по-

и в рассматриваемом плоском случае полностью определяет поле скоростей

компонент скорости перемещения границы и поля скоростей. Это условие отражает материальность свободной границы, скорость изменения которой относительно составляющих ее материальных точек равна нулю:

35

Стоит обратить внимание на нелинейность полученного условия.

Это (чисто кинематическое) граничное условие содержит неизвестную функцию (x,t) , определенную на границе, – профиль свободной границы. Поэтому задача требует еще одного условия на свободной границе, в качестве которого выступает первый интеграл по z уравнения динамики:

в рамках принятых выше ограничений на жидкость называемый интегралом Лагранжа ( g – ускорение свободного падения). Граничные условия по x обычно подразумевают условие отсутствия возмущений на бесконечно удаленных краях:

Итак, имеем уравнение (5.2) с граничными условиями (5.3)-(5.6). Сначала рассмотрим линеаризованную постановку краевой задачи:

где звездочка обозначает комплексное сопряжение. Аргумент kx t называют фазой. Из (5.7) получаем уравнение для определения R :

R k 2 R 0 ,

общее решение которого

R Aexp(kz) B exp( kz)

36

с учетом (5.8) принимает вид

R 2Ach(kz) .

Подставляя последнее в уравнение (5.10), получаем дисперсионное соотно-

шение

и в нулевом приближении выражение (5.13) приобретает вид c0 gh .

Мы используем c0 как характерную скорость. Принимая за характерный масштаб длины h , введем характерное время h / c0 . Теперь можно обезразмерить задачу (5.2)–(5.6), рассматривая безразмерные зависимые и независи-

определить из (5.4), откуда c0h . Вид уравнений (5.2)–(5.6) в обезразмеренных переменных при этом практически не изменится (в уравнении (5.5) исчезнет множитель g ), поэтому далее черта над безразмерными переменными опускается, размерные переменные нам больше не понадобятся.

В рамках слабонелинейной постановки задачи мы будем принимать гипотезу (5.14). Разлагая дисперсионное соотношение (5.12) в ряд по малому обезразмеренному волновому числу kh , получим:

37

и волновой аргумент (5.11) примет вид

Выражение (5.15) позволяет увидеть длинноволновые («медленные») переменные, в масштабах которых развивается нелинейная волна:

Здесь для удобства введено обозначение для малого параметра, kh . Волновое число k имеет смысл обратной длины волны ; в случае непериодического решения в виде уединенной волны за можно принять ширину ее профиля, соответствующую половине ее высоты, поэтому

n 0

Подставляя (5.17) в (5.7), получаем:

( n ,x zn n(n 1) n zn 2 ) 0 .

n 0

Выделяя в этом уравнении множители при линейнонезависимых степенях z и приравнивая их нулю, получаем рекуррентную систему дифференциальных связей, налагаемых на n :

(5.18) следует, что и 2k 1 0, k 1,2,... вместе со всеми нечетными коэффициентами разложения. Теперь (5.17) превращается в ряд

Представленный таким образом потенциал скоростей удовлетворяет уравнению (5.2) и граничному условию на дне. В граничных условиях (5.4), (5.5) фигурируют выражения

38

где f 0 ,x , на свободной границе принимающие вид

Вграничных уравнениях (5.21), (5.22) искомые функции , f , связанные

свозмущением, малы по сравнению с единицей. Для слабонелинейной версии модели в этих уравнениях имеет смысл оставить члены, содержащие нелинейности минимального порядка и дисперсию (описываемые производными по координате выше второго порядка):

Далее эта система граничных уравнений в частных производных будет исследоваться методом многих масштабов. Запишем разложения по малому параметру:

где p – действительное положительное число, и выражения частных производных через независимые переменные , (см. выражения (5.16)):

После подстановки (5.24), (5.25) в (5.23) получим:

39

p 1 0 , p 3 0 , 2 p 1 1, 2 p 3 1, p 1 f0 , 2 p 1 f1,

2 p 1( f0 0 , 0 f0 , ) 3 p 1( f0 1, 1 f0 , ) ... 16 p 3 f0 , 0;

p 1 f0 , p 3 f0 , 2 p 1 f1, 2 p 3 f1, t p 1 0 , 2 p 1 1,

2 p 1 f0 f0 , 3 p 1 f0 f1, ... 12 p 3 f0 , ... 0.

Выше мы опустили слагаемые большего порядка малости по сравнению с оставшимися. В полученных уравнениях приведем подобные при различных степенях и выпишем коэффициенты при них:

и т.д. Невыписанные слагаемые, очевидно, имеют более высокий порядок малости по сравнению с выписанными. Легко увидеть, что в данной последовательности все члены, начиная со второго, независимо от значения p , превосходят степень первого p 1. Параметром p поэтому можно распорядиться, приравняв две из оставшихся степеней. При этом с нелинейно-волновой точки зрения содержательный результат получится тогда, когда в одни уравнения попадут производные по времени, нелинейные и дисперсионные члены, «разбросанные» по некоторым двум разным степеням. Нелинейность

вуравнении локализует, а дисперсия «размазывает» решение в пространстве;

врезультате баланса этих механизмов рождаются представляющие интерес стабильные пространственно-временные структуры. Таким образом, приравнивая 2 p 1 и p 3 (откуда p 2 ), получаем интересный случай, рассмот-

ренный Кортевегом и де Фризом. В этом случае для членов рядов (5.24) получаем последовательно решаемые системы уравнений:

40