Математическое моделирование в естественных науках.-1

Список литературы

1.De Gennes P.G., Prost J. The Physics of Liquid Crystals. – Oxford: Clarendon Press, 1993. – 596 p.

2.Brochard F., de Gennes P.G. Theory of magnetic suspensions in liquid crystals // J. Phys. – 1970. – Vol. 31. – P. 691–708.

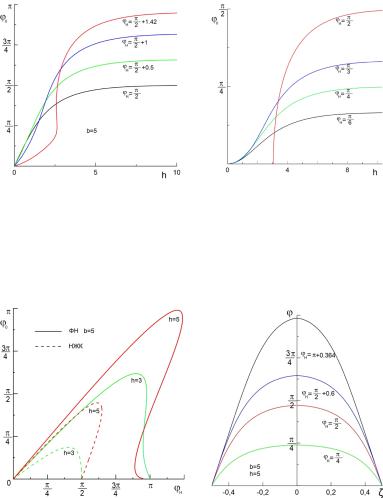
3.Райхер Ю.Л., Бурылов С.В., Захлевных А.Н. Ориентационная структура и магнитные свойства ферронематика во внеш-

нем поле // ЖЭТФ. – 1986. – Т. 91. – С. 542–551.

ДИНАМИКА АНСАМБЛЯ СФЕРИЧЕСКИХ ЧАСТИЦ ПОД ДЕЙСТВИЕМ ПОСТУПАТЕЛЬНЫХ ВИБРАЦИЙ ЛИНЕЙНОЙ ПОЛЯРИЗАЦИИ

О.О. Фатталов1, 2, Ю.М. Маслова1, Т.П. Любимова1, 2

1Пермский государственный национальный исследовательский университет,

Пермь, Россия, fattalov@mail.ru,

2Институт механики сплошных сред УрО РАН, Пермь, Россия

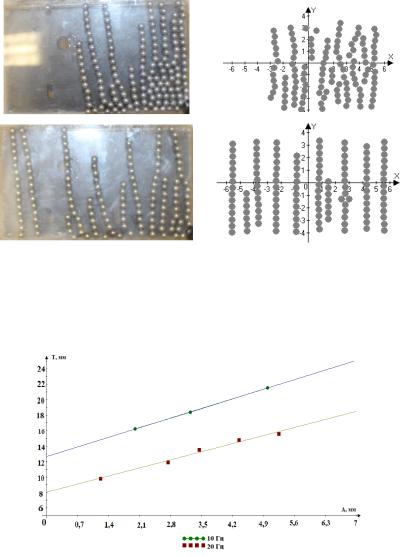
Исследуется динамика ансамбля твердых частиц, взвешенных в колеблющейся вязкой жидкости, под действием поступательных высокочастотных малоамплитудных вибраций. Исследование проводится численно в двумерном приближении и экспериментально. Получены данные о влиянии параметров вибраций и свойств жидкости на характеристики возникающих структур.

Ключевые слова: ансамбль частиц, вязкая жидкость, вибрации, численное исследование, экспериментальное исследование.

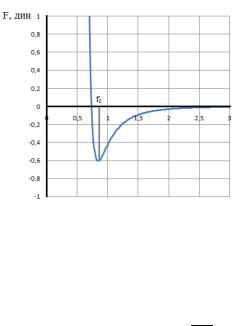
В настоящей работе рассмотрена многофазная система, представляющая собой вязкую жидкость со взвешенными в ней твердыми частицами. Сосуд с жидкостью подвергается поступательным вибрациям линейной поляризации. Известно, что под действием вибрационной силы две сферических частицы, погруженные в невязкую или маловязкую жидкость, притягиваются, если вибрации перпендикулярны линии, соединяющей центры частиц, и отталкиваются, если вибрации па-

392

раллельны линии, соединяющей центры частиц [1]. При увеличении вязкости знак силы взаимодействия между частицами меняется на противоположный. В случае большого числа частиц под действием вибрационной силы частицы формируют специфические структуры [2].

Математическое моделирование поведения частиц в колеблющейся вязкой жидкости проводилось с помощью метода молекулярной динамики, являющегося одним из наиболее мощных вычислительных методов, эффективно применяемых для моделирования физических и биологических систем.

Рис. 1. Зависимость расстояния взаимодействия пары частиц в вязкой жидкости от расстояния между частицами F (r)

Решались уравнения движения частиц, записанные в виде

Rs = Vs ,ms Vs = Fs − bVs , s = 1, N,

где b – коэффициент диссипации. Сила (рис. 1) справедлива для расстояний, больших по сравнению с размером частиц. На расстояниях порядка толщины вязкого скин-слоя сила меняет знак, и частицы начинают отталкиваться. Для описания этого эффекта

393

выражение для силы, полученное в невязком приближении, было дополнено еще одним слагаемым, меняющим знак силы на малых расстояниях:

численного моделирования динамики системы стальных шариков в водном растворе глицерина, в колеблющемся сосуде при сле-

ций сосуда, r0 = 2, 25 мм – радиус частицы, ρ = 1, 2 103 кг/м3 – плотность жидкости, ρ0 = 7,8 103 кг/м3 – плотность вещества частиц, ν = 8,7 10−6 м2/c – кинематическая вязкость жидкости. Найдено, что действие вибраций на первом достаточно коротком этапе приводит кформированиюкластеров, состоящихиз нескольких частиц. Дальнейшая эволюция системы состоит в формировании линейных цепочек, ориентированных перпендикулярно направлению вибраций.

Как видно из рис. 2, результаты математического и экспериментального моделирования близки. Это позволяет сделать вывод, что используемые модель и программа расчетов адекватно описывают реальное поведение систем и пригодны для расчетов в области параметров, недоступных в эксперименте.

Дальнейшие эксперименты включали две серии. В первой серии исследовался диапазон параметров вибраций, при которых в жидкости формируются периодические структуры. Найдено, что формирование структур, представляющих собой линейные цепочки, возможно в диапазоне от 5 до 27 Гц. При частотах, больших 27 Гц, частицы собираются у одной из стенок кюветы.

394

Вторая серия экспериментов проводилась с 50 % водным раствором глицерина с плотностью ρ = 1,126 103 кг/м3

икинематической вязкостью ν = 3,2 10−6 м2/c, в который помещалось 250 стальных сферических частиц радиусом r0 = 2,25 мм

иплотностью ρ0 = 7,8 103 кг/м3. На рис. 3 приведены полу-

ченные в этой серии экспериментов зависимости пространственного периода T формирующихся структур (расстояния между цепочками) от амплитуды вибраций при различных фиксированных значениях частоты вибраций. Как видно из рисунка, при фиксированной частоте вибраций пространственный период структур растет с увеличением амплитуды вибраций по закону, близкому к линейному. Сопоставление кривых, полученных при разных частотах, показывает, что пространственный период структур растет с увеличением частоты вибраций.

Работа выполнена при финансовой поддержке Российского научного фонда (грант 14-21-00090).

Список литературы

1. Lyubimov D.V., Cherepanov A.A., Lyubimova T.P. The motion of solid body in a liquid under the influence of a vibrational field // Reviewed Proc. of the First Int. Symp. on Hydromechanics and Heat/Mass Transfer in Microgravity. – Gordon and Breach. – 1992. – Р. 247–251.

2. Chain formation of spheres in oscillatory fluid flows / D. Klotsa, M.R. Swift, R.M. Bowley, P.J. King // Phys. Rev. – 2009. – E 79, 021302.

396

МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ОСАЖДЕНИЯ НАНОПЛЕНОК НА ТЕМПЛАТАХ ПОРИСТОГО ОКСИДА АЛЮМИНИЯ

А.Ю. Федотов1, А.В. Вахрушев2, А.В. Северюхин1, Р.Г. Валеев3

1Институт механики УрО РАН, Ижевск, Россия, alezfed@gmail.com, 2Ижевский государственный технический университет

им. М.Т. Калашникова, Ижевск, Россия, vakhrushev-a@yandex.ru,

3Физико-технический институт УрО РАН,

Ижевск, Россия, rishatvaleev@mail.ru

Рассматриваются некоторые вопросы формирования нанопленочных покрытий на подложках пористого оксида алюминия. В работе проводится анализ структуры подложки и нанопленки. Тип осаждаемых атомов варьируется. В качестве потенциала при моделировании использовался модифицированный метод погруженного атома. Построены динамические характеристики заполнения поры осаждаемыми атомами.

Ключевые слова: эпитаксия, нанопленки, моделирование, LAMMPS, кристаллическая структура, молекулярная динамика.

Пористый анодный оксид алюминия (АОА) благодаря гекса- гонально-упорядоченному расположению вертикально-ориенти- рованных к поверхности пленки пор нашел широкое применение в качестве темплатов для синтеза наноструктур различного вида: нанопроволок, наноточек, наноколец, нанотрубок и других [1]. Также АОА может быть с успехом использован вкачестве носителей каталитически активных наночастиц [2] и наноструктур полупроводников. Это позволяет сформировать упорядоченные массивы наноструктур полупроводникового люминофора одинакового размера и формы, чтобы представить каждый нанообъект в качестве отдельного излучателя света. Когерентное сложение излучения от всех источников приведет к существенному увеличению интенсивности света [3].

Задача моделирования формирования нанопленочных покрытий решалась в несколько этапов. На первом этапе происходит формирование подложки из аморфного оксида алюминия. Атомы алюминия и кислорода в необходимой пропорции (2:3)

397

помещаются в расчетную ячейку с периодическими граничными условиями по бокам (рис. 1, а). Под воздействием потенциальных сил при нормальных термодинамических условиях подложка стабилизируется и приходит в состояние покоя (рис. 1, б). Стабилизация подложки обусловлена именно потенциальными силами, так как ее формирование происходит за счет самоорганизации атомов алюминия и кислорода. При этом тепловые флуктуации и диффузия в рамках заданной температуры в сформировавшейся подложке присутствуют, но существенной перестройки ее структуры не происходит, атомы незначительно колеблются вблизи занятых положений.

На втором этапе в подложке вырезается отверстие – пора требуемого радиуса и глубины (разрез подложки с порой показан на рис. 1, в). Впоследствии эта пора будет заращиваться атомами различного типа (рис. 1, г).

Рис. 1. Этапы решения задачи формирования нанопленочных покрытий на основе пористого оксида алюминия

В силу периодических граничных условий по направлениям x и y в работе рассматривалась только одна пора. В горизонтальных направлениях периодические граничные условия предусматривают параллельный перенос расчетной ячейки. Сверху и снизу моделируемая система находилась под воздействием жестких граничных условий. При приближении атомов к верхней границе исследуемой системы имитировался их отскок от жесткой стенки. Снизу положения атомов в тонком слое вблизи границы расчетной ячейки жестко зафиксированы.

398

В данной работе шаг интегрирования по времени составил 1 фс. Общее время при моделировании системы для этапа стабилизации (см. рис. 1, а) составило порядка 0,5 нс, для этапа релаксации (см. рис. 1, б, 1, в) – 0,2 нс и для этапа осаждения (см. рис. 1, г) – 0,2 нс. Заращивание пористой подложки осуществлялось равномерным напылением атомов по нормали по отношению к подложке. В течение стадии заращивания в области над подложкой добавлялись осаждаемые атомы. Их положение над подложкой определялось равномерным случайным законом распределения. Управляющими параметрами процесса являлись количество добавляемых атомов в единицу времени и их общее число. Начальная скорость осаждаемых атомов была постоянной. Скоростные параметры менялись только при взаимодействии осаждаемых атомов с подложкой. Для проведения тестовых расчетов рассматривались отдельная наноструктура в безвоздушной среде и ее динамика во время релаксационной самоорганизации атомов.

Для проведения теоретических исследований использовался пакет программ для параллельных вычислительных процессов

LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator). Задача осаждения нанопленок решалась при помощи потенциала MEAM (модифицированный методпогруженногоатома).

В результате проведенных исследований установлены различные варианты эпитаксиального заращивания пористых подложек на основе оксида алюминия различными типами атомов. Для разных типов осаждаемых атомов были зафиксированы разные процессы взаимодействия наноструктур и механизмы заращивания подложек и пор. Для всех типов осаждаемых атомов наблюдались единичные атомы, которые достигали дна поры. Наиболее полное и плотное заращивание поры было зафиксировано при эпитаксии галлия. Пора, заполненная атомами, может рассматриваться как квантовая точка и использоваться для получения оптических и электрических эффектов.

При исследовании заращивания атомами галлия покрытий с порами различного размера было получено, что активный

399

рост количества атомов в поре происходит в период времени 20–120 пкс. Заращивание поры после 120 пкс времени конденсации сопровождается перестройкой атомарной структуры, что соответствует стабилизации зависимостей и небольшим уменьшением процента атомов галлия, проникших внутрь поры. Кроме того, стабилизация центра масс осаждаемых атомов происходит на разной глубине поры. Для пор радиусом 2 и 3 нм центр масс формируется выше середины глубины поры (рис. 2). С ростом размера поры центр масс начинает образовываться вблизи середины глубины поры. Дальнейший рост радиуса поры (больше 5 нм) существенного влияния на центр масс уже не оказывает, пора уже достаточно плотно заполнена осаждаемыми атомами.

Рис. 2. Процент попавших в пору атомов Ga по отношению к общему числу осажденных атомов для пор разного диаметра

Методики осаждения наноразмерных пленок могут быть в дальнейшем использованы для технологических процессов изготовления оптических материалов и могут применяться для прогнозирования и проектирования нанопленок.

Исследование выполнено при финансовой поддержке РНФ

(проект № 15-19-10002).

400