
Математическое моделирование и проектирование систем автоматики
..pdfэтом значение функции в этой точке сохраняется в параметре Y. При отрицательном значении этого произведения корни на участке от А до С существуют, поэтому это половина диапазона подвергается дальнейшему анализу, для чего точка В переносится в точку С.
Новый диапазон области существования корней подвергается анализу на соответствие заданной точности. Если абсолютное значение разности диапазона от В до А будет равно заданной абсолютной точности ε или меньше нее, то середина этого диапазона может быть приближенным корнем заданного уравнения. Следовательно, алгоритм вычисляет результат середины интервала и выводит его, после чего он прекращает свою работу. В случае несоответствия этого условия алгоритм переходит на очередную итерацию деления диапазона существования корней, которая выполняетсявышеописанным способом.
2.6.Принцип и алгоритм численного решения системы алгебраических уравнений
Под решением системы алгебраических уравнений понимают множество значений аргументов, при которых все функции системы имеют одно и то же значение. Такие решения называют еще корнями системы алгебраических уравнений. Система считается решенной, если найдены все значения корней.
В классическом (точном) варианте решения такой системы составляется матрица из коэффициентов всех уравнений системы, на основе которой находится конечный результат. Указанный способ достаточно трудоемкий, поэтому в математических моделях используют другой приближенный численный метод такого решения. Суть его заключается в следующем.
Общий вид системы n-го порядка может быть представлен
как
a11x1 + a12x2 + a13x3 + … + a1nxn = b1, |
|
a21x1 + a22x2 + a23x3 + … + a2nxn = b2, |
(21) |
a31x1 + a32x2 + a33x3 + … + a3nxn = b3, |
|
81
………………………………
an1x1 + an2x2 + an3x3 + … + annxn = bn.
Решение каждого из этих уравнений определяется как |
|
|||||||
x1 |
= |
1 |
|
|
(b1 – a12x2 – a13x3 – … – a1nxn), |
|
||
|
a |
|
||||||
|
|
|
|
|
|
|||
|
|
11 |
|
|
|
|
||
x2 |
= |
|
1 |
|
(b2 – a21x1 – a23x3 – … – a2nxn ), |
|
||
|
|
|
|
|||||
|
|
a22 |
|
|
|
|||
x3 |
= |
1 |
|
|
(b3 – a31x1 – a32x2 – … – a3nxn), |
(22) |
||
|
a33 |
|
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
....................... |
|
|
xn= |
1 |
(bn – an1x1 – an2x2 – … – an – 1xn – 1). |
|
|||||
|
|
|||||||
|
ann |
|
|
|
||||
Если решение каждого предыдущего уравнения вставить в последующее, то любой k-й корень этой системы с некоторой точностью может быть определен из следующего выражения:
xk= |
(bk −∑n |
aki xi ) |
(23) |
|
i=1 |
|
. |
||
|
|
|
||
|
ann |
|
||
По этой формуле решение системы уравнений численным методом с заданной точностью можно найти, если первоначально задаться некоторым исходным значением корней моделируемой системы, а затем каждое последующее значение этих корней определять из следующего уравнения:
|
(bk −∑n |
aki xi ) |
(24) |
|
xk = |
i=1 |
|
+ xk-1, |
|
|
|
|
||
|
ann |
|
||
где xk – 1 − значение корня на предыдущей итерации; xk − значение корня на текущей итерации.
Графически принцип итерационного метода поиска корней системы можно показать на примере системы из двух уравнений (рис. 29).
82

Рис. 29. Графическое изображение системы двух линейных уравнений
На рис. 29 изображены две линейные алгебраические зависимости, решение которых нужно найти приближенным итерационным методом. Для этого произвольно выберем начальное значение корня уравнения (1) (рис. 29). Пусть это будет аргумент Х0. Вставим это значение в уравнение (2) (см. рис. 29). В этом случае первое приближенное решение этой системы будет Х0, Х1 при значении обеих функций, равном Y0. При этом решении системы интервал от Х0 до Х1 будет намного превышать заданный диапазон точности решения, поэтому вставим значение аргумента Х1 в уравнение (2) (см. рис. 29) и, проецируя значение Y1 на линию уравнения (1) (см. рис. 29), получим при данном значении функции решение Х1, Х2 для следующей итерации. Диапазон между корнями Х1 и Х2 при этом значительно сужается.
Продолжая подобную операцию, можно добиться того, чтобы расстояние между корнями этой системы уравнений укладывалось в заданный диапазон.
Реализация этого принципа определения на ЭВМ корней системы алгебраических уравнений представлена алгоритмом, показанным на рис. 30. После запуска этого алгоритма вводятся следующие параметры:
– n − число уравнений в системе (порядок системы);
83

–A(n, n+1) − двумерный массив коэффициентов системы;
–X(n) − начальное значение корней системы;
–ε − заданная точность решения.
начало |
n, A(n,n+1), X(n), ε |
K = 1, n |
S = 0 |
J = 1, n |
S = S + A(k, j) * Xj |
X1k = (Bk – S) / Akk + Xk |
Tk = |X1k – Xk| / X1k |
Xk = X1k |
K = 1, n |
нет |
K = 1, n |
|
|
Tk <= ε |
|
|
Xk |
конец |
|
да |
|
Рис. 30. Алгоритм определения корней системы алгебраических уравнений
84
После завершения ввода исходных данных открывается вложенный цикл с заданным числом повторений по параметру К, который изменяется от 1 до n, а внутренний цикл по параметру J меняется в тех же пределах.
Во внутреннем цикле этого вложенного процесса формируется сумма произведения коэффициентов каждого уравнения системы на соответствующее текущее значение корней системы (первоначально это начальные значения этих корней). Эта сумма накапливается в параметре S.
После выхода из внутреннего цикла во внешнем цикле по формуле (23) производится вычисление уточненного значения всех n корней, а также точности диапазона их расположения. Во внешнем цикле сохраняется значение корней, полученных на текущей итерации для того, чтобы использовать их значения на последующей итерации. После выхода из внешнего цикла открывается следующий цикл проверки заданного диапазона расположения корней (заданной точности). Если заданный диапазон текущего и предыдущего значений хотя бы по одному из корней будет нарушен, то алгоритм возвращается к новому итерационному вложенному циклу их уточнения. В противном случае отдельным циклом корни выводятся на печать.
2.7. Принцип и алгоритм численного дифференцирования
Дифференциалом dy функции f(x) называется приращение ординаты касательной этой функции, проведенной из точки начала этого приращения (рис. 31).
Производной функции называют отношение ее дифференциала dy (приращения ординаты касательной) к приращению аргумента dx:
y ' = |
dy |
. |
(25) |
|
|||
|
dx |
|
|
Геометрически производная – это тангенс угла α наклона касательной к приращению аргумента ∆x (см. рис. 31).
85

Численное дифференцирование функции производится через вычисление полинома, структура которого зависит от числа точек (узловых значений функции) на участке приращения аргумента. Эти значения функции на участке дифференцирования называют узлами.
Рис. 31. Изменение дифференциала dy и приращения функции ∆y на участке приращения аргумента ∆x
Если число этих узлов равно трем, то вычисление полинома производится по схеме, представленной на рис. 32, а.
При численном дифференцировании вводится некоторый параметр р, который вычисляется по следующей формуле:
p = |
x − x0 |
, |
(26) |
|
h |
||||
|
|
|
где x0 − начальное значение аргумента при дифференцировании; x − конечное значение аргумента при дифференцировании; h − шаг дифференцирования.
С учетом выражения (26) при дифференцировании функции с числом узлов, равным трем, используется следующий полином:
y' (x0 − p h) = |
1 |
[(h −0,5)y−1 −2p y0 +( p +0,5)y1] . |
(27) |
|
h |
||||
|
|
|
86

а |
б |
в |
Рис. 32. Схема вычисления полинома при численном дифференцировании функции
При дифференцировании функции с числом узлов, равным четырем, при вычислении полинома используется расчетная схема, представленная на рис. 32, б. В этом случае полином вычисляется по следующей формуле:
y |
' |
(x |
− p h) = |
1 |
[− |
3p2 −6p +2 |
y |
−1 |
+ |
3p2 −4p −1 |
y |
0 |
− |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
0 |
|
|
h |
|
|
6 |
|
|
|
|
|
2 |
|
|
(28) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3p2 |
−2p −2 |
|
|
|
3p2 −1 |
|
|
|
|
|
|
|
|
|
|
||||
− |
y |
|
+ |
y |
]. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
1 |
|
6 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При дифференцировании функции с числом узлов, равным пяти, при вычислении полинома используется расчетная схема, представленная на рис. 32, в. В этом случае полином вычисляется по следующей формуле:
y |
' (x − p h) = |
1 |
[ |
2p3 −3p2 − p +1 |
y |
|
− |
4p3 −3p2 −8p +4 |
y |
|
+ |
||||||||
|
|
−2 |
|
|
−1 |
||||||||||||||
|
0 |
|
|
|
h |
12 |
|
|
|
6 |
|
|
|
(29) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2p3 −5p |
|
|
|
|
4p3 |
−3p2 −8p −4 |
|
|
|
2p3 +3p2 − p −1 |
|
|
|
|||||
+ |
y |
|
+ |
y + |
y |
]. |
|
|
|||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|
|
6 |
1 |
|
|
12 |
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
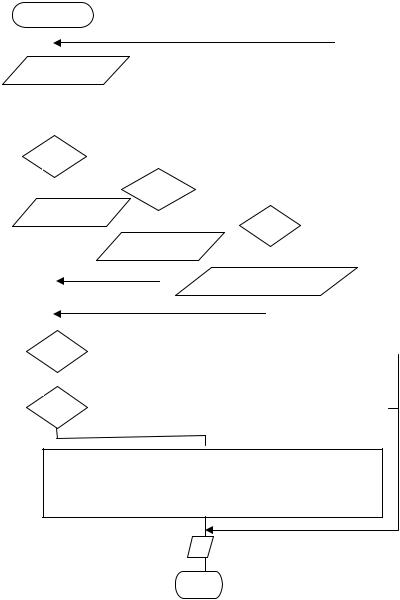
Алгоритм численного дифференцирования функции показан на рис. 33.
После пуска этого алгоритма необходимо задать следующие параметры: число точек (узлов) дифференцирования N, шаг дифференцирования функции h и диапазон ее дифференцирования от x0 до x.
87
начало
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N, h, X0, X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P = ( |
X – X0) / h |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
не |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
N=3 |
|
|
|
|
нет |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
да |
|
|
|
|
|
|
|
|
N=4 |
|
|
|
нет |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Y–1, Y0, Y1 |
|
|
|
|
|
||||||||||||||
|
|
|
|
да |
|
|
|
|
|
|
|
|
||||||||
|
|
|
N=5 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Y–1, Y0, Y1, Y2 |
да |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
да |
|
|
|
|
|
Y–2,Y–1,Y0,Y1,Y2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||||||
нет |
N=3 |
|
|
|
|
F = ((P – 0,5)Y–1 – 2P Y0 +(P–0,5)Y1) / h |
|
|
||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
N=4 |
|
|
|
|
F = (–(3P2 – 6P + 2)Y–1 /6 + (3P2 – 4P–1) Y0 /2 + |
|
|||||||||||||
|
|
|
|
+ (3P2 – 2P–2) Y1 /2 + (3P2 – 1) Y2 /6) / h |
|
|||||||||||||||
|
|
|
||||||||||||||||||
нет
F= ((2P3 – 3P2 – P –1) Y–2 /12 – (4P3 – 3P2 – 8P + 4)Y–1 /6 +
+(2P3 – 5P)Y0 / 2 – (4P3 –3P2 – 8P – 4)Y1 /6 + (2P3 + 3P2 –
– P –1) Y2 /12
F
конец
Рис. 33. Алгоритм численного дифференцирования функции
88
На основе этих данных по формуле (26) вычисляется параметр p, который затем вставляется в формулу конкретного полинома при вычислении дифференциала. Далее алгоритм анализирует величину параметра N и в зависимости от его значения требует ввода соответствующего числа значений функций в выбранных точках. После ввода необходимого числа значений функций с помощью алгоритма по соответствующей формуле полинома вычисляется величина дифференциала.
2.8. Принцип и алгоритм численного вычисления определенного интеграла
Графически определенный интеграл некоторой функции представляет собой площадь фигуры, ограниченной графиком этой функции, осью абсцисс и осями ординат, проведенными из точек нижнего и верхнего пределов интегрирования. Численно, но приближенно с заданной точностью эта площадь может быть вычислена методом сложения элементарных площадей, на которые можно поделить площадь указанной фигуры. В зависимости от вида фигуры этих элементарных площадей различают множество методов приближенного вычисления определенного интеграла. Мы рассмотрим только два из них – это метод прямоугольников и метод трапеций.
По методу прямоугольника (рис. 34, а) площадь подинтегральной фигуры заменяется суммой площадей прямоугольников, основание которых равно шагу интегрирования Н, а высота определяется значением функции в точке приращения аргумента на величину этого шага.
Величина шага приращения аргумента определяется как
H = |
B − A |
, |
(30) |
|
N |
||||
|
|
|
где В – верхний предел интегрирования; А – нижний предел интегрирования; N – число участков от А до В.
Элементарная площадь подинтегрального прямоугольника равна
89

Si= f(x)H. |
(31) |
Сумма всех элементарных площадей прямоугольников |
|
подинтегральной функции определяется по формуле |
|
N |
|
S = ∑[ f (A) + f (A + H ) +... + f (A + H (N −1)]H . |
(32) |
i=1
аб
Рис. 34. Схема вычисления определенного интеграла методом прямоугольника (а) и методом трапеций (б)
По этой формуле строится структура алгоритма, представленного на рис. 35. После пуска этого алгоритма необходимо задать пределы интегрирования и число интервалов N разбиения диапазона интегрирования функции. Вводится также заданная точность вычисления.
Сумма элементарных площадей накапливается в переменных S и S1, которые предварительно обнуляются. Затем вычисляется шаг Н приращения аргумента по формуле (30). Перед началом цикла суммирования аргумент принимает значение нижнего предела интегрирования. После этого в цикле в переменной S накапливается сумма значений функции на каждом шаге приращения аргумента, после выхода из цикла эта сумма умножается на параметр Н, в результате чего вычисляется сумма площадей элементарных прямоугольников подинтегральной функции в пределах интервала ее интегрирования.
90
