Математическое моделирование и проектирование систем автоматики

ППЧ

i = 1, N

ППЧ

i = 1, N

FK4, i = h*fi;

Yi = Zi +(FK1, i + 2FK2, i + 2FK3, i+ выход +FK4, i)/6Zi = Yi

Рис. 41. Структура подпрограммы «RGK» алгоритма Рунге – Кутта

101

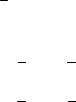
После выхода из подпрограммы к параметру К добавляется единица и его значение сравнивается с параметром Кр. В случае равенства К и Кр производится вывод результата (X и Y), после чего параметр К обнуляется. Если это условие не выполняется, то алгоритм (прежде чем выйти на очередную итерацию) проверяет другое условие, по которому параметр X не должен превышать параметра Xk, в противном случае аргумент достигнет своего конечного значения и алгоритм останавливается.

Алгоритм работы подпрограммы «RGK» начинается с обращения к другой подпрограмме «ППЧ», в которой вычисляются правые части системы дифференциальных уравнений. Вычисленные значения правых частей уравнений используются при вычислении соответствующих коэффициентов по формулам (47–50), которые вставляются затем в формулу (46).

Расчет этих коэффициентов для системы уравнений производится в цикле, число итераций которого равно порядку N этой системы. В каждом цикле по формуле yi = zi + fk1,i/2 рассчитывается промежуточное значение параметра yi, которое уточняется в каждом из этих циклов.

Подпрограмма правых частей «ППЧ» представляет собой последовательность присвоений переменной совокупности алгебраических вычислений, соответствующих правым частям системы дифференциальных уравнений, т.е.

102

f1 = выражение 1,

f2 = выражение 2, (51) f3 = выражение 3,

fn= выражение n.

Этот процесс повторяется четыре раза при каждом вычислении коэффициента fkj.

Вычисление корней системы дифференциальных уравнений методом Рунге – Кутта обеспечивает точность вычисления пропорциональной пятой степени шага интегрирования, т.е.

ε= h5.

Кнедостатку метода Рунге – Кутта нужно отнести невозможность использовать его для решения уравнений высших порядков (два и более), поэтому в случае наличия таких уравнений используют метод понижения порядка дифференциального уравнения, суть которого состоит в том, что производная высокого порядка заменяется любой другой переменной, как правило первого порядка.

2.9.6. Решение дифференциальных уравнений высших порядков по методу Рунге – Кутта

Суть метода понижения порядка дифференциального уравнения состоит в том, что производная высокого порядка заменяется любой другой переменной и на основе этой переменной записывается новое дифференциальное уравнение, как правило первого порядка.

Например, для понижения порядка уравнения

произведем в нем замену следующего вида:

После этого исходное уравнение приобретет вид

103

После такой замены дифференциальное уравнение высокого порядка заменяется системой уравнений первого порядка, при этом число уравнений в системе равно порядку исходного уравнения. Поэтому в нашем примере такая система будет иметь вид

dydt + y =0,

Таким образом, для уравнений порядка выше двух необходимо будет производить несколько замен переменных. Число этих замен равно степени дифференциального уравнения.

104

3. АНИМАЦИОННЫЕ МОДЕЛИ СИСТЕМ АВТОМАТИКИ

Развитие возможностей электронных вычислительных машин позволило совершенствовать возможности математических моделей. Это проявилось, прежде всего, в том, что их наглядность стала соизмеримой с наглядностью оригинальных процессов.

Реализация возможностей анимации в математических моделях стала реальностью только тогда, когда ЭВМ получила возможность вывода информации в графическом режиме, а это в свою очередь стало возможным при наличии в структуре ЭВМ достаточных ресурсов ее оперативной памяти.

Наряду с появлением графического режима работы ЭВМ совершенствовалось и ее программное обеспечение применительно к возможностям работы ЭВМ в графическом режиме. Это привело к появлению программ, позволяющих выдавать результат вычисления не только в цифровом варианте, но и в графической форме. При этом качество графического результата (машинной графики) определялось ресурсом оперативной памяти ЭВМ.

В свою очередь принципы организации машинной графики позволили по новому организовать пользовательский интерфейс самой ЭВМ. Так называемые окна, а по сути дела графические объекты, позволили довольно просто управлять ее вычислительным процессом.

Принципы машинной графики в сочетании с возможностями мультипликации и принципами построения мнемосхем технологических процессов легли в основу реализации анимационных моделей.

Анимационной моделью называют такую разновидность математической модели физического процесса, демонстрация результата которой реализована на принципах сочетания машинной графики и анимационной мультипликации.

105

3.1.Принципы организации анимационных моделей

Воснову работы анимационных моделей заложены принципы сочетания:

– результата решения математической модели;

– машинной графики;

– мультипликации.

Результат математического моделирования может быть отображен командами машинной графики конкретного алгоритмического языка. В частности, на языке «Паскаль» это может быть сделано с помощью следующих команд:

1)putpixal (x,y.f) − изображение точки на экране дисплея;

2)line to (x,y) или line (x1,y1,x2,y2) − изображение линии на экране дисплея;

3)rectangle (x1,y1,x2,y2) − изображение прямоугольника на экране дисплея;

4)circle (x,y,r) − изображение окружности на экране дисплея;

5)arc (x,y,φ0,φi,r) − изображение дуги на экране дисплея;

6)sector (x,y, φ0,φi) − изображение сектора на экране дисплея.

Анимационное изображение процесса перемещения точки

по полю носителя информации осуществляется командой putpixal (x,y.f). В этой команде: x, y – координаты точки; f –цвет точки.

Часто в анимационных моделях совокупностью таких команд могут изображаться как символы, так и отдельные фигуры. Примеромэтому можетслужитьизображение символа (буквы) П.

Обычно для изображения буквенных символов используют точечную матрицу. В нашем примере мы используем такую матрицу размером 5×7. Буква П в этой матрице выглядит так, как показано на рис. 42.

Для последовательного вывода точек, использующихся для изображения этого символа, команда putpixal (x,y.f) приме-

106

няется во вложенном цикле. Алгоритм вывода этого символа выглядит следующим образом (рис. 43).

Внешний цикл этой вложенности открывается по параметру Y с числом повторений, равным 7. Этим циклом контролируется положение точек символа П по вертикали. Внутренний цикл этой вложенности открывается по параметру Х с числом повторений, равным 5. Этим циклом контролируется положение точек указанного символа по горизонтали. Обычно координата (Х = 0, Y = 0) соответствует точке, расположенной в верхнем левом углу матрицы, поэтому во внутреннем цикле по

107

истинности условия Y = 0 командой putpixal (x,y.f) выводятся на печать все точки верхней строки буквенной матрицы. После первого выхода из внутреннего цикла условие Y = 0 становится ложным, поэтому проверяется следующее условие (Х = 0)OR(Х = 4), по которому командой putpixal (x,y.f) точки ставятся только в позиции ноль и четыре во всех остальных строках матрицы.

Анимационное изображение процесса перемещения линии

по полю носителя информации может осуществляться одной из следующих команд: lineto (x,y) и line (x1,y1,x2,y2).

По команде lineto(x,y) линия по полю носителя информации перемещается от точки положения на нем курсора до точки с координатами x, y. По команде line(x1,y1,x2,y2) эта линия перемещается от точки с координатами x1,y1, до точки с координатами x2, y2. В обоих случаях цвет линии предварительно задается командой setcolor(f), где f – код соответствующей цветовой гаммы.

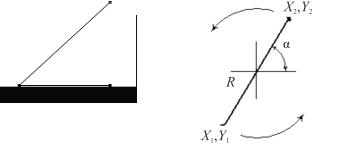
Рассмотрим варианты использования этой команды в анимационных моделях на следующем примере. Первоначально обеспечим удлинение исходной линии с поворотом ее на 45 ○.

X2, Y2

X1, Y1 X2, Y2

Рис. 44. Графическое отображение результата выполнения команды line (x1,y1,x2,y2)

В этом фрагменте примера командой line (x1,y1,x2,y2) в цикле происходит приращение параметров Х2 = Х2+1 и

108

Y2 = Y2+1 при этом параметры Х1 и Y1 остаются неизменными (см. рис. 44, а). В следующем фрагменте этого примера первоначально повернутая на 45 ○ прямая линия начинает вращаться вокруг своего центра симметрии (рис. 44, б).

При этом радиус поворота определяется значением параметров Х2, Y2 при горизонтальном положении прямой из выражения

В результате этого поворота координаты концов прямой линии меняются следующим образом:

Y1 = R + R sin(180 −α).

В третьем фрагменте этого примера концы горизонтальной прямой линии совершают круговое движение относительно оси Х. Схема этого фрагмента выглядит следующим образом (рис. 45).

Рис. 45. Результат пространственного измерения положения прямой в соответствии с уравнениями (58)

Величина радиуса вращения концов этой прямой заранее задается. Исходя из величины этого радиуса определяется значение параметра Y1, которое зависит от величины угла β поворота вращающегося конца этой линии.

109

В результате поворота на угол β от 0 до 3600 координаты концов этой линии меняются следующим образом:

Все фрагменты этого примера описываются алгоритмом, представленном на рис. 46.

После запуска этого алгоритма вводятся исходные данные, среди которых координаты исходной прямой (X1, Y1, X2, Y2) и радиус прецессии вращения ее торцов R1. Следующим оператором line(x1,y1,x2,y2) изображается эта исходная прямая и производится расчет по формуле (56) радиуса ее последующего вращения.

Первым анимационным процессом с этой прямой является процесс трансформации ее длины и углового положения относительно осей координат. Этот процесс осуществляется в цикле. Счетчиком этого цикла является параметр Х2, величина которого меняется от 1 до 10. В этом цикле одновременно меняются параметры Х2 и Y2, поэтому прямая линия за десять циклов одновременноувеличивается вразмереи наклоняетсякосиХ.

В следующем цикле анимация этой прямой связана с ее вращением, которое происходит в плоскости координат Х, Y относительно точки ее середины. Этот поворот осуществляется в диапазоне изменения угла от 45 до 180о. При этом положение координат (X1, Y1, X2, Y2) этой прямой вычисляется в соответствии с формулами (57).

На последнем этапе анимации происходит циклическое вращение этой прямой, наклоненной к оси Х под углом α. Положение координат (X1, Y1, X2, Y2) этой прямой вычисляется по формулам (58).

При этом торцы этой прямой совершают вращательное движение по кругу с радиусом R1. Полный оборот этого процесса завершается в цикле за 360о, после чего программа завершается.

110