
Функции комплексного переменного и операционное исчисление
..pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Пермский национальный исследовательский политехнический университет»
Р.Ф. Валеева, Р.Х. Спицына
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО И ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Утверждено Редакционно-издательским советом университета
в качестве учебно-методического пособия
Издательство Пермского национального исследовательского
политехнического университета
2016
1
УДК 517.53+517.445](072.8) В15
Рецензенты:
канд. пед. наук, доцент В.Л. Пестерева (Пермский государственный гуманитарнопедагогический университет);
канд. физ.-мат. наук, доцент В.А. Соколов (Пермский национальный исследовательский политехнический университет)
Валеева, Р.Ф.
В15 Функции комплексного переменного и операционное исчисление : учеб.-метод. пособие / Р.Ф. Валеева, Р.Х. Спицына. – Пермь : Изд-во Перм. нац. исслед. политехн. ун-та, 2016. – 100 с.
ISBN 978-5-398-01661-1
Приведены основные определения, формулировки теорем и формулы, используемые при решении задач, а также даны решения типовых задач и варианты индивидуальных расчетных заданий.
Содержание пособия соответствует учебным программам курса высшей математики для технических университетов.
Предназначено для студентов вузов, изучающих разделы «Функции комплексного переменного» и «Операционное исчисление».
УДК 517.53+517.445)(072.8)
ISBN 978-5-398-01661-1 |
© ПНИПУ, 2016 |
2
Глава I
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
1.1. Комплексные числа и действия над ними
Комплексным |
числом z называется выражение вида |
z x iy , где x, y |
– действительные числа, а i – мнимая еди- |
ница, удовлетворяющая условию i2 1.
Выражение z x iy называется алгебраической формой записи комплексного числа. Числа x и y называются соответственно действительной и мнимой частями комплексного числа
|
z и обозначаются x Re z, |
y Im z . |
|
|
|||
|
|
Комплексное |
число z x iy называется |
сопряженным |
|||
комплексному числу z x iy . |
|
|
|||||
|
|
Два комплексных числа z1 x1 iy1 |
и z2 x2 |
iy2 равны то- |
|||
гда и только тогда, когда |
y |
|
|
||||
|
x1 x2 , |
y1 y2 . |
|
|
|
||
|
|
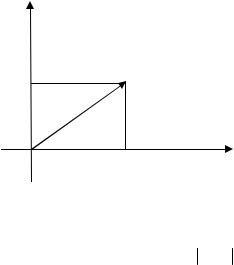
Геометрически ком- |
|
|
|
||
плексное число z x iy |
|
|
|
||||
изображается на плоско- |
|
M(x,y) |
|||||
сти x0 y точкой M x, y |
|
|
|
||||
либо |
радиус-вектором |
r |
|
|
|||
|
|
этой точки (рис. 1.1). |
|
|
|
||
|
OM |
|
|
|
|||
Ось Ох называется дейст- |
0 |
|
x |
||||
вительной осью, |
Оу – |
|
Рис. 1.1 |
|
|||
мнимой. |
|
|
|
|
|||
|
|
r и точки, изображающей ком- |
|||||
|
|
Полярные координаты |
|||||
плексное число на плоскости, называются соответственно модулем и аргументом комплексного числа. Обозначают: r x iy ,
Arg z .
3

Аргумент комплексного числа определяется с точностью до слагаемого, кратного 2 .
Главное значение аргумента комплексного числа обозначается как arg z : arg z .
Очевидно, что
Arg z arg z 2 k ,
где k Z .
Модуль и аргумент комплексного числа z x iy находятся по формулам:
r |
|
x2 y2 , |
|
|
tg |
y |
, причем |
|||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
y |
|
если x 0, |
|
|
|||||
|
arctg |
|
, |
|
|
|||||||||
|
x |
|
|
|||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
, если x 0, y 0, |
|||||||
|
arctg |
|
|
|||||||||||
|
x |
|||||||||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
arg z |
|
|
|
|
|
|
|
|
, если x |
|
y 0, |
|||
arctg |
|
|
0, |
|||||||||||
|
x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
если |
x 0, y 0, |
|
|
||||||||
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
, |
если |
x 0, y 0. |
|
||||||||
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Любое комплексное число z x iy можно записать в тригонометрической форме:
zr cos isin
ив показательной форме:
z rei ,
где r z , Arg z , ei cos isin (формула Эйлера).
4

Сложение, вычитание и умножение комплексных чисел в алгебраической форме записи аналогичны действиям над многочленами. При делении комплексных чисел числитель и знаменатель умножают на число, сопряженное со знаменателем:
z1 z2 x1 iy1 x2 iy2 x1 x2 i y1 y2 , z1 z2 x1 iy1 x2 iy2 x1 x2 i y1 y2 ,
z1 z2 x1 iy1 x2 iy2 x1 x2 y1 y2 i x1 y2 x2 y1 ,
z1 |
|
z1 z2 |
|
x1 iy1 x2 iy2 |
|
x1 x2 y1 y2 |
i |
x2 y1 x1 y2 |
. |
z2 |
|
x2 iy2 x2 iy2 |
x22 y22 |
|
|||||
|
z2 z2 |
|
|
x22 y22 |
|||||
Если числа z1 и z2 заданы в тригонометрической форме:
z1 r1 cos 1 i sin 1 , z2 r2 cos 2 isin 2 ,
то
z1 z2 |
r1 |
r2 |
cos 1 2 isin 1 |
2 , |
|||||||
|
z1 |
|
|
r1 |
cos 1 2 isin 1 2 ; |
||||||
|
|
r |
|||||||||
|
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
zn |
rn cos n isin n , где n N ; |
|||||||||
|
n |
z |
|
n |
|
|
2k |
isin |
2k |
||
|
|
|
r cos |
n |
n |
, |
|||||
|
|
|
|
|
|
|
|
|
|
||
где n N , k 0,1,2,...,(n 1) .
Из действий над комплексными числами в тригонометрической форме вытекают следующие свойства модулей и аргументов комплексных чисел:
z1 z2 |
|
|
|
z1 |
|
|
|
z2 |
|
, |
аrg z1 z2 аrg z1 аrg z2 ; |
|
|
|
|
|
5

|
|
|
|
|
|
z1 |
|
|
|
|
|
|
z1 |
|
|
, аrg |
|
z1 |
|
аrg z аrg z |
2 |
, |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
z2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
аrg zn n аrg z, |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
zn |
|
|
|
z |
|
n , |
|
|
|
|
|
n N . |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Замечание. Значениям |
|
n |
z отвечают точки на плоскости |
|||||||||||||||||||||||||||||||||||||||||||||
x0 y , расположенные в вершинах правильного |
n -угольника, |
|||||||||||||||||||||||||||||||||||||||||||||||
вписанного в окружность радиуса n r |
с центром в начале коор- |
|||||||||||||||||||||||||||||||||||||||||||||||
динат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример |
1.1. Выполнить |
действия: |
а) |
|
2 i 3 2i ; |
|||||||||||||||||||||||||||||||||||||||||||
б) 2 i 3 2i ; в) |
|
|
|
|
3 i |
; г) i23 ; д) 2 3i8 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
2 3i |
|
|
|
|
|
|
|
|
1 i7 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а) 2 i 3 2i 2 3 i 1 2 1 i ; |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
б) 2 i 3 2i 6 3i 4i 2i2 6 i 2 8 i ; |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
в) |
3 i |
|
|
3 i 2 3i |
|
|
|
|
6 2i 9i 3i2 |
|
|
6 11i 3 |
3 |
11 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 13 ; |
||||||||||||||||||||||||||
2 3i |
2 3i 2 3i |
|
|
|
|
|
4 9i2 |
|
|
|
4 9 |
|
13 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
г) i23 i i22 |
|
i |
|
|
|
i2 |
|
|
11 i |
|
|
1 |
11 i ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2 3i |
8 |
|
|
2 3 i2 4 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 i |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|||||||||||||||||||
д) 1 i7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 i |
|
|
|
1 |
|
2 |
|
. |
||||||||||||||||||
|
1 i i2 3 |
1 i |
1 i 1 i |
|
2 |
|
2 |
|||||||||||||||||||||||||||||||||||||||||
Пример 1.2. Найти модуль и аргумент следующих чисел:
а) 1 i ; б) |
|
3 i |
; в) 1 i 3 |
; г) 2 ; д) |
2 i ; е) i ; ж) |
1 . |
|||||
Решение. |
|
|
|
|
3 |
2 |
|||||
|
|
|
|
|
|
||||||
а) |
|
1 i |
|
|
|
1 1 |
2, tg 1, |
arg( 1 i) arctg1 |
|
||
|
|
|
|||||||||
|
|
3 ; |
|
|
|
|
|||||
4 |
|
|
4 |
|
|
|
|
||||
6

|
|
|
|
|
|
|
|
|
|
3 i |
|
|
|
|
|
|
|
|
|
|
|
3 i) |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
б) |
|
|
|
|
|
|
3 |
1 2, |
arg( |
arctg |
|
|
|
|
6 |
; |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
в) |
|
|
|
1 i |
3 |
|
2, |
arg( 1 i |
3) arctg( |
3) |
|
|
|
2 |
; |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
г) |
|
|
|
|
2 |
|
|
2, |
arg( 2) ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
д) |
|
|
2 |
|
i |
|
|
2 |
, |
|
|
|
2 |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
3 |
|
|
3 |
|
arg |
3 |
i |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
е) |
|
|
|
|
i |
|
|
|
1, |
|
arg( i) ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
ж) |
|
|
|
|
|
|
|
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
2 |
|
|
|
2 |
, arg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Пример 1.3. Выполнить действия в тригонометрической |
||||||||||||||||||||||||||||||||||||||||||||||||
форме: |
|
|
|
|
|
|
3 i 7 |
1 i 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
1 i 3 3 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Решение. Найдем модуль и аргумент каждого из чисел, |
||||||||||||||||||||||||||||||||||||||||||||||||
входящих в данные выражения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
3 i |
|
2, |
|
arg |
|
3 i arctg |
|
|
|
|
|
6 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 i |
|
2, |
arg 1 i arctg 1 |
|
; |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 i |
|
|
3 |
|
2, |
arg 1 i |
3 arctg |
3 |
|
|
2 . |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z , |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Обозначим |
искомое |
число |
тогда, используя |
свойства |
||||||||||||||||||||||||||||||||||||||||||||
модулей и аргументов, находим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
z |
|
|
|
|
27 |
|
|
|
|
|
2 4 |
2 |
6 |
64 , |
arg z 7 |
|
|
|
|
3 |
|
|
|
2 |
|
|
37 |
, |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
3 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
6 |
4 |
|
|
3 |
|
6 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
7
z 64 |
|
37 |
isin |
37 |
|
64 |
|
|
isin |
|
|
|
cos |
6 |
6 |
|
cos |
6 |
6 |
|
|||||
|
|
|
|
|
|
|
|
|
||||
64 |
|
3 |
i 1 |
|
32 |
3 i . |
|
|
|
||||||
|
|||||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
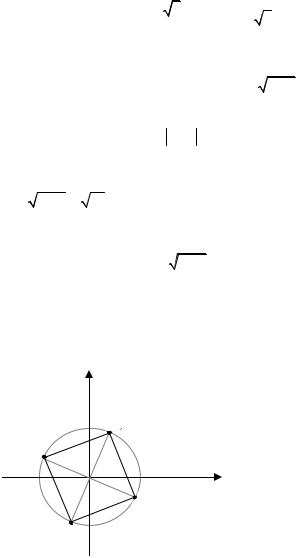
Пример 1.4. Найти все значения 4 16i , изобразить их на плоскости.
Решение. Находим 16i 16, arg( 16i) 2 ,
|
|
|
|
2k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
2k |
|
|
|
|
|
||||||||
4 16i 4 16 |
cos |
|
|
|
i sin |
|
|
|
|
|
, где k 0,1,2,3 . |
||||||||||
|
|
4 |
|
|
|
4 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, для 4 16i |
получаем четыре значения: |
|
|
||||||||||||||||||
|
z0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
cos |
8 |
|
isin |
8 |
, |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
z |
2 |
cos |
3 i sin |
3 , |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
8 |
|
8 |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
7 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
isin |
, |
||||||
|
|
|
|
|
|
|
|
|
|
|
2 cos |
8 |
8 |
|
|||||||
|
Z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
z |
2 |
cos |
11 isin 11 . |
||||||||
z2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
8 |
|
8 |
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
|
|
|
|
|
x |
|
|
|
|
Геометрически |
точки |
|||||||||
|
z0 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
расположены в вершинах |
|||||||||||||
z3 |
|
|
|
|
|
|
|
|
|
квадрата, вписанного в ок- |
|||||||||||
|
|
|
|
|
|
|
|
|
ружность |
радиусом |
2 |
с |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
Рис. 1.2 |
центром в начале коорди- |
|
нат (рис. 1.2). |
||
|
8

1.2. Задание множества точек на комплексной плоскости
Различные множества E комплексных чисел z задаются с помощью равенств или неравенств, или их систем. Эти множества удобно строить, исходя из геометрической интерпретации заданных соотношений.
Пример 1.5. Определить множество точек плоскости, заданное соотношениями:
а) z R ; б) z R ; в) r z R ; г) arg z ; д) arg z ;
е) a Re z b ; ж) a Im z b ; з) |
|
z z0 |
|
R . |
|
|
Решение. |
|
|
|
|
|
|
|
|
|
а) z x iy, |
|
z |
|
|
x2 y2 , |
|
x2 y2 R2 . |
||
|
|
||||||||
Таким образом, равенство |
|
z |
|
R определяет множество |
|||||
|
|
||||||||
точек, лежащих на окружности радиусом R с центром в начале координат;
б) |
|
|
z |
|
R – множество точек, лежащих внутри круга радиу- |
|||||||||
|
|
|
||||||||||||
сом R с центром в начале координат; |
|
|||||||||||||
в) |
|
|
r |
|
z |
|
|
|
R – кольцо между концентрическими окружно- |
|||||
|
|
|
|
|||||||||||
стями радиусами r и R с центром в начале координат; |
||||||||||||||
г) |
|
arg z , – луч, выходящий из начала координат |
||||||||||||
под углом к оси 0x ; |
|
|
||||||||||||
д) |
|
arg z , |
– множество точек, заключенных |
|||||||||||
между двумя лучами; |
|
|
||||||||||||
е) |
|
|
a Re z b , |
Re z x, |
a x b |
– полоса между прямы- |
||||||||
ми x a и x b ; |
|
|
|
|||||||||||
ж) |
|
|
a Im z b , |
Im z y, |
a y b |
– полоса между прямы- |
||||||||
ми y a и y b ; |
|
|
|
|||||||||||
з) |
|
z z0 |
|
R – окружностьрадиусом R сцентром вточке z0 . |
||||||||||
|
|
|||||||||||||
9
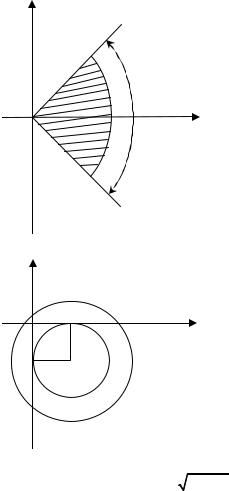
Пример 1.6. Изобразить на комплексной плоскости область, заданную неравенствами:
а) |
|
|
z |
|
1, |
|
|
|
|
arg z |
|
; б) |
2 |
|
z 2 2i |
|
3 ; |
||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||
в) |
|
|
z 4 |
|
|
|
|
z 4 |
|
5 ; г) |
0 arg z 1 i |
. |
|||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
4 |
|||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
y
0
|
|
а) Область, заданная |
не- |
||||||
|
|
равенствами |
|
z |
|
1, |
|
|
|
|
|
|
|
4 |
|||||
|
arg z |
, |
|
|
|
|
|
||
изображена |
на |
||||||||
4 |
|
4 |
|
|
|
|
|
|
|
|
|
рис. 1.3. Точки, лежащие на |
|||||||
|
x |
окружности, |
не принадлежат |
||||||
|
|
области, поэтому эта часть |
|||||||
|
|
границы |
области |
отмечена |
|||||
штриховой линией; |
|
|
|||||||
4 |
|
|
|||||||
|
б) Центр кольца есть точ- |
||||||||
|
|
||||||||
|
|
ка z0 2 2i , |
область изобра- |
||||||
Рис. 1.3 |
жена на рис. 1.4; |
|
|
|
|
||||
y |
|
|
в) Равенство |
|
z 4 |
|
|
||
|
|
||||||||
|
|
z 4 |
|
5 означает, что сум- |
|||||
|
|
|
|||||||
|
|
|
|||||||
0 2
-2 z0
Рис. 1.4
Имеем a 5, c 4,
|
ма |
расстояний |
от |
точки |
z |
|
x |
до |
точек |
4 и |
4 |
равна |
5 . |
|
Геометрическое |
место таких |
||||
|
точек есть эллипс с фокусами |
|||||
|
в точках 4 и 4 и с большей |
|||||
|
полуосью a 5 . |
|
|
|
||
|
|
Значит, неравенство в) |
||||
|
задает |
область, |
лежащую |
|||
|
внутри эллипса (рис. 1.5); |
|
||||
b a2 |
c2 |
3 . |
|
|
|
|
10
