§2.7. Кривые второго порядка на плоскости.

2.7.1. Определение. Кривой второго порядка на плоскости называется множество точек плоскости, которое описывается уравнением второго порядка, то есть

(2.24)

где

2.7.2. Определение. Канонической системой координат для данной кривой называется декартова система координат, в которой уравнение кривой имеет наиболее простой вид.

2.7.3. Определение. Уравнение кривой в канонической системе координат называется ее каноническим уравнением.

2.7.4. Эллипс.

2.7.4.1. Определение. Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух данных точек, называемых фокусами, является постоянной величиной.

2.7.4.2. Каноническое уравнение эллипса.

Введем на плоскости прямоугольную систему координат. Направим ось Ох вдоль линии, соединяющей фокусы F₁ и F₂, с серединой отрезка F₁F₂, а ось Оу – перпендикулярно через середину отрезка F₁F₂.

Пусть расстояние между фокусами равно 2с, а сумма расстояний от фокусов до произвольной точки равна 2а(a>c).

Тогда фокусы имеют координаты и, и, если– текущая точка эллипса, то расстояния от этой точки до фокусов равны длинам фокальных радиусовF₁M и F₂M: и. Тогда из определения эллипса

.

Возведем обе части уравнения в квадрат:

После преобразований получим:

Возводя обе части уравнения в квадрат, имеем:

откуда

.

Обозначая , перепишем последнее уравнение в виде

, и после деления на правую часть окончательно получим

. (2.25)

Это уравнение называется каноническим уравнением эллипса.

2.7.4.3. Свойства эллипса.

1. Из уравнения (2.25) следует, что , это означает, что график эллипса ограничен прямоугольником.

2. Так как в уравнение входят только четные степених,у, то если точка (х,у) принадлежит эллипсу, (т.е. х,у удовлетворяют уравнению), то точки (х,у), (х,у), (х,у) тоже принадлежат уравнению. Следовательно, оси Oх и Оу являются осями симметрии эллипса, точка О(0, 0) является центром симметрии.

3. Рассмотрим часть эллипса, расположенную в первом квадранте (). Решив уравнение относительноу, получим .

Если x= 0, то у=b; если x=а, то у= 0; у убывает при возрастании х;.

На Рис. 2.18 изображен график эллипса.

Замечание.

1. Число а называют большой полуосью эллипса, b – малой полуосью.

2. Числоназывается эксцентриситетом эллипса. Этот параметр характеризует степень «сжатия» эллипса. Если(т.е.с = 0, b = а) фокусы эллипса совпадают с его центром, полуоси равны и эллипс превращается в окружность. Если () эллипс вырождается в отрезок, соединяющий фокусы.

3. Если провести через фокусы ось Оу и провести аналогичные рассуждения, то фокусами являются точки и, точкаудовлетворяет уравнению

,

откуда получим каноническое уравнение эллипса

,

где малая полуось . В этом случае эксцентриситет, большая полуось расположена на осиОу (Рис. 2.19).

2.7.5. Гипербола.

2.7.5.1. Определение. Гиперболой называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух данных точек, называемых фокусами, является постоянной величиной.

2.7.5.2. Каноническое уравнение гиперболы.

Вывод канонического уравнения гиперболы аналогичен соответствующему выводу для эллипса.

Введем на плоскости прямоугольную систему координат. Направим ось Ох вдоль линии, соединяющей фокусы F₁ и F₂, с серединой отрезка F₁F₂, а ось Оу – перпендикулярно через середину отрезка F₁F₂.

Пусть расстояние между фокусами равно 2с, а модуль разности расстояний от фокусов до произвольной точки равен 2а(a<c).

Тогда фокусы имеют координаты F₁(-c, 0)и F₂(c, 0), и, если – текущая точка эллипса, то расстояния от этой точки до фокусов равны длинам фокальных радиусовF₁M и F₂M:

,

.

Тогда из определения гиперболы

, то есть.

Избавимся от иррациональности в полученном уравнении

Обозначая , получим уравнение

, (2.26)

которое и будет каноническим уравнением гиперболы.

2.7.5.3. Свойства гиперболы.

1. Из уравнение (2.26) следует, что ; следовательно, гипербола имеет две ветви.

2. Поскольку в уравнение входят только четные степени х, у, оси Oх и Оу являются осями симметрии гиперболы, а точка О(0, 0) является центром симметрии.

3. В первом квадранте . Еслиx = а, то у = 0; у возрастает вместе с х. При больших х функция - бесконечно малая, и ей можно пренебречь, т.е. прямаяявляется наклонной асимптотой при(строго это можно показать методами математического анализа). Вследствие симметрии прямаяявляется асимптотой гиперболы и при, по той же причине прямаятакже является двусторонней асимптотой.

Кривая, имеющая эти свойства, изображена на Рис. 2.20.

Параметр а называют действительной полуосью гиперболы, параметр b –мнимой полуосью. Ось, имеющая с гиперболой две общие точки (на Рис. 2.20 ось Ох) называется действительной осью гиперболы. Ось, не имеющая общих точек с гиперболой, называется мнимой осью гиперболы. Число называетсяэксцентриситетом гиперболы. Так как a<c, то .

Замечание.

Если расположить фокусы гиперболы на осиОу: F₁(0, -c),F₂(0,c)(Рис. 2.21), произвольная точка гиперболы будет удовлетворять уравнению

, b<c,

параметр а вводится соотношением , эксцентриситет гиперболы, действительная полуось гиперболы будет равнаb, мнимая – а, каноническое уравнение примет вид

.

В этом случае действительной осью гиперболы будет ось Оу, а мнимой – ось Ох.

2.7.6. Парабола.

2.7.6.1. Определение. Параболой называется геометрическое место точек плоскости, равноудаленных от заданной точки, называемой фокусом параболы и заданной прямой этой плоскости, называемой директрисой.

2.7.6.2. Каноническое уравнение параболы.

Пусть на плоскости задана точка F (фокус параболы) и прямая (директриса параболы). Расстояние между фокусом и директрисой равно р(параметр параболы). Проведем ось Ох через фокус перпендикулярно директрисе в направлении от директрисы к фокусу, а ось Оу – параллельно директрисе через середину отрезка, соединяющего фокус с точкой пересечения директрисы и оси абсцисс (Рис 2.22).

Пусть произвольная точка принадлежит параболе. Тогда из определения параболы в координатной форме получим:

.

После возведения в квадрат и очевидных преобразований имеем

. (2.27)

Это уравнение называется каноническим уравнением параболы.

2.7.6.3. Свойства параболы.

1. Из уравнение (2.27) видно, что ; следовательно, график параболы расположен в правой полуплоскости.

2. Поскольку в уравнение входит только четная степень у, ось Oх является осью симметрии параболы.

Замечание.

Если направить ось абсцисс через фокус перпендикулярно директрисе в направлении от фокуса к директрисе, то уравнение параболы будет иметь вид

.

Если же расположить ось ординат параллельно директрисе, то мы получим соответственно

и

в зависимости от направления оси ординат (от директрисы к фокусу или от фокуса к директрисе, соответственно). Вышеописанные случаи расположения параболы на плоскости и их соответствующие канонические уравнения приведены на Рис. 2.23.

2.7.7. Смещенные кривые второго порядка.

Рассмотрим, как преобразуются уравнения эллипса, гиперболы, параболы, если их центры не совпадают с началом системы координат, но оси остаются параллельными координатным осям. Рассмотрим, например, эллипс с центром в точке с координатами (х₀,у₀),изображенный на Рис. 2.24. В координатах

полученных в результате параллельного переноса, уравнение эллипса имеет канонический вид

.

Таким образом, в исходных координатах уравнение смещенного эллипса будет

. (2.28)

Аналогично для смещенных гипербол уравнения будут иметь вид или; (2.29)

для смещенных парабол:

, ,

или . (2.30)

2.7.8. Общее уравнение кривой второго порядка.

2.7.8.1. Определение. Уравнение вида

(2.31)

называется общим уравнением кривой второго порядка.

Рассмотрим возможные знаки коэффициентов и.

2.7.8.2. Определение. Уравнение вида (2.31) называется уравнением эллиптического типа, если коэффициенты при старших степенях имеют один знак, т.е. .

2.7.8.3. Исследование уравнения эллиптического типа.

Выделим в уравнении (2.31) полные квадраты. Предположим, что (в противном случае уравнение можно умножить на -1).

Получим:

,

где .

Выполним параллельный перенос системы координат:

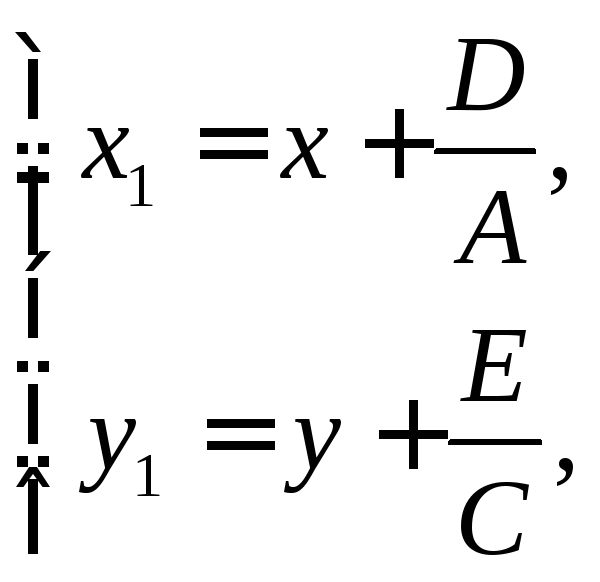
тогда уравнение примет вид

.

Возможны три случая:

1. если , то уравнение

имеет единственное решение, то есть эллипс вырождается в точку (0,0);

2. если , получим

,

где ,, то есть уравнениеэллипса;

3. если , то уравнение может быть преобразовано к виду

,

где ,. Очевидно, полученное уравнение не имеет действительных решений. В этой связи обычно говорят, что уравнение характеризуетмнимый эллипс.

2.7.8.4. Определение. Уравнение вида (2.31) называется уравнением гиперболического типа, если коэффициенты при старших степенях имеют разные знаки, т.е. .

2.7.8.5. Исследование уравнения гиперболического типа.

Предположим без ограничения общности, что . Как и при исследовании уравнения эллиптического типа, выделим полные квадраты. Получим уравнение

, ,

причем снова имеем три возможных случая:

1. если , получаем каноническое уравнениегиперболы

,

с действительной полуосью , мнимой полуосью.

2. Если , получаем уравнение. Раскладывая левую часть уравнения на множители, получим уравнениепары пересекающихся прямых . Можно считать, что в этом случаегипербола вырождается в асимптоты.

3. Если , то уравнение преобразуется к видугиперболы с мнимой полуосью , действительной полуосью.

2.7.8.6. Определение. Уравнение вида (2.31) называется уравнением параболического типа, если один из коэффициентов при старших степенях равен нулю, т.е. .

2.7.8.7. Исследование уравнения параболического типа.

Будем считать для определенности, что . Уравнениепредставим в виде

Возможны следующие случаи:

1. Е= 0. Тогда .

Если правая часть этого уравнения положительна , то, т.е. уравнение определяетпару параллельных прямых. Если , получаемпару совпавших прямых . Если правая часть отрицательна, имеемпара мнимых прямых.

2. . Приведем уравнение к виду

.

Если обозначить, и произвести параллельный перенос осей координат

получим каноническое уравнение параболы в зависимости от знака коэффициента.

Лекция 8.