Лекция 4.

Глава 2. Аналитическая геометрия на плоскости и в пространстве.

В этой главе мы изучим фигурах первого и второго порядка на плоскости и в пространстве.

§2.1. Декартова прямоугольная система координат.

2.1.1. Определение. Аффинной (декартовой) системой координат в трехмерном пространстве называется совокупность некоторой точки и произвольного базиса. При этом точка называется началом координат, а прямые, проходящие через начало координат в направлении базисных векторов – осями координат: первая – осью абсцисс (ОХ), вторая – осью ординат (ОY), третья – осью аппликат (OZ).

Замечание.

Аналогично определяются аффинные системы координат на плоскости и прямой.

2.1.2. Определение. Вектор, соединяющий начало координат с некоторой точкой, называется радиусом-вектором этой точки.

2.1.3. Определение. Координатами точки в аффинной системе координат называются координаты ее радиуса-вектора.

2.1.4. Определение. Аффинная система координат, базис которой является ортонормированным, называется прямоугольной декартовой системой координат.

2.1.5. Параллельный перенос осей.

Пусть новая система координат получена из старойсдвигом на вектор. Тогда

. Базисные орты в обеих системах одинаковы, поэтому координаты вектора есть координаты точкиО’ в новой системе координат:

2.1.6. Кривые и поверхности.

Одним из основных вопросов аналитической геометрии является исследование линий на плоскости и поверхностей в пространстве.

2.1.6.1. Определение. Уравнение f(x, y) = 0 называется уравнением линии l на плоскости, если этому уравнению удовлетворяют координаты х, у всех точек М(х, у), лежащих на линии, и не удовлетворяют координаты ни одной точки P(х, у), не лежащей на кривой:

f(x, y) = 0 М(х, у)l,

f(x, y) 0М(х, у)l.

2.1.6.2. Определение. Уравнение F(x, y, z) = 0 называется уравнением поверхности в пространстве, если этому уравнению удовлетворяют координаты х, y, z всех точек М(х, у, z), лежащих на поверхности, и не удовлетворяют координаты ни одной точки P(х, у, z), не лежащей на поверхности:

F(x, y, z) = 0 М(х, у, z) ,

F(x, y, z) 0М(х, у, z) .

2.1.7. Две основные задачи аналитической геометрии.

I. Дано некоторое множество точек плоскости (пространства), обладающее некоторым набором свойств. Требуется составить уравнение (или систему уравнений), которое в некоторой системе координат задает это множество точек.

II (обратная). В заданной системе координат некоторое множество точек плоскости (пространства) описывается заданным уравнением (или системой уравнений). Требуется определить вид и основные свойства этого множества и построить его эскиз.

§2.2. Простейшие задачи аналитической геометрии.

2.2.1. Нахождение длины отрезка.

Пусть в заданной декартовой прямоугольной системе координат имеется две точки и. (Рис. 2.2).

Вектор .

Следовательно, длина отрезка .

2.2.2. Деление отрезка в заданном отношении.

Г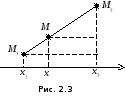оворят, чтоточка М делит отрезок М₁М₂ в отношении , если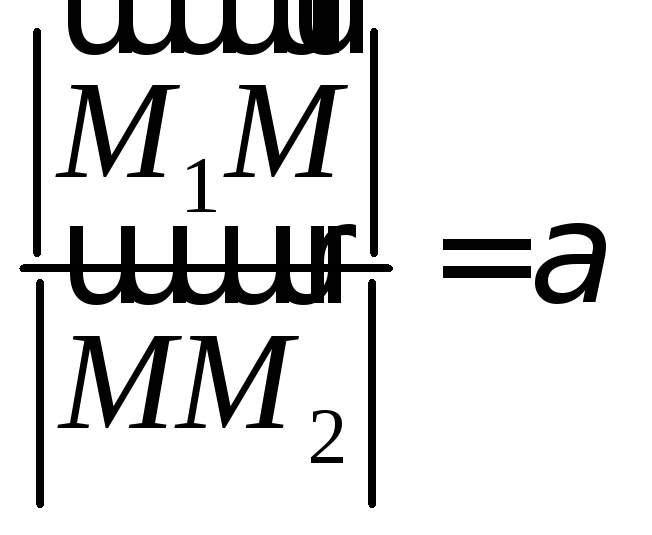. Найдем координаты точкиМ. На Рис. 2.3 изображен отрезок и его проекция на ось Ох.

Запишем векторное равенство и его проекции на оси координат.

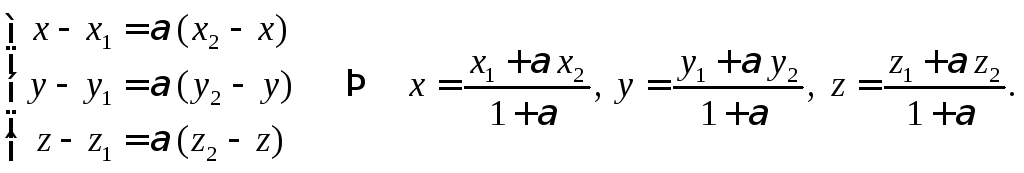
В частном случае , т.е. когда точкаМ – середина отрезка, получаем, что координаты середины отрезка равны средним арифметическим координат концов: