
Глава_3_Ангем
.docЛекция 9.
Глава 3. Линейные пространства
В этой главе мы приведем краткие сведения о линейных пространствах, которые затем будут использованы в главе 5 при исследовании систем линейных алгебраических уравнений.
§3.1. Понятие линейного пространства.
3.1.1.
Определение. Множество
L,
содержащее элементы произвольной
природы
![]() ,…,
называется линейным
пространством,
а его элементы – векторами
линейного пространства,
если
,…,
называется линейным
пространством,
а его элементы – векторами
линейного пространства,
если
-
задана операция сложения элементов L, т.е. каждой паре элементов
 множества
L
можно поставить в соответствие элемент
множества
L
можно поставить в соответствие элемент
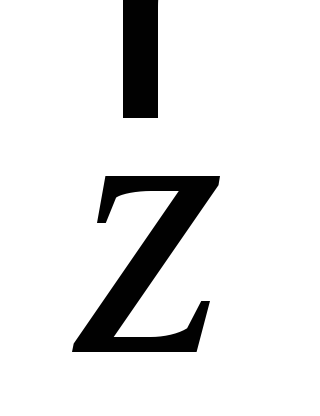 ,
называемый суммой элементов:
,
называемый суммой элементов:
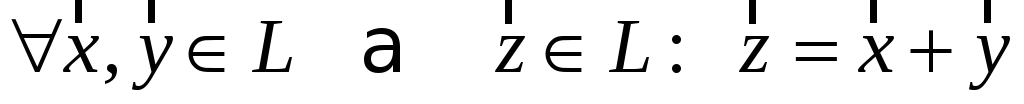 ;
; -
задана операция умножения элементов L на действительные числа, т.е. каждому элементу
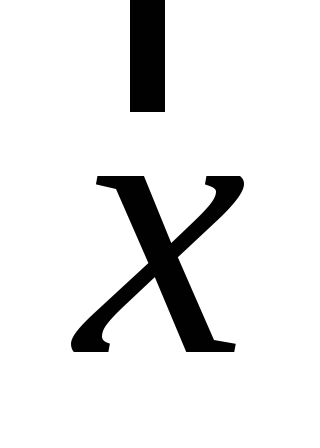 множества
L
и числу
множества
L
и числу
 можно
поставить в соответствие элемент
можно
поставить в соответствие элемент
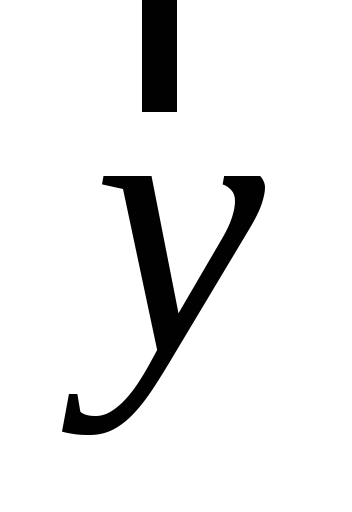 ,
называемый произведением элемента
,
называемый произведением элемента
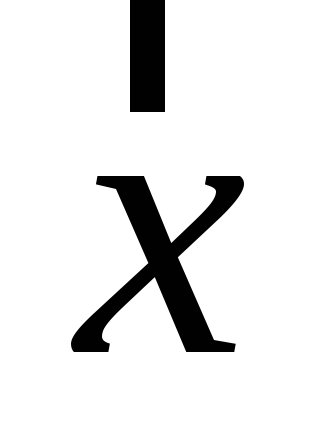 на число
на число
 :
:
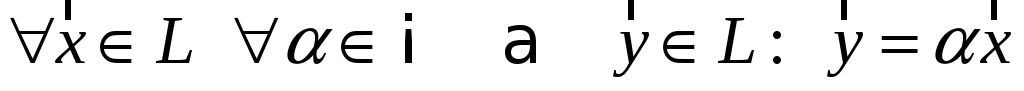 ;
; -
для указанных операций справедливы свойства, называемые также аксиомами линейного пространства:
1.
![]() (коммутативность операции сложения)
(коммутативность операции сложения)
2.
![]() (ассоциативность операции сложения)
(ассоциативность операции сложения)
3.
![]() (существование нулевого вектора)
(существование нулевого вектора)
4.
![]() (существование противоположного
вектора)
(существование противоположного
вектора)
5.
![]() (унитарность)
(унитарность)
6.
![]() (ассоциативность операции умножения
на число)
(ассоциативность операции умножения
на число)
7.
![]() (дистрибутивность по числам);
(дистрибутивность по числам);
8.
![]() (дистрибутивность по векторам).
(дистрибутивность по векторам).
Замечание. Из указанных аксиом вытекают следующие дополнительные свойства векторов линейного пространства:
а) единственность нулевого вектора;
b) единственность противоположного элемента;
c) свойства нулевого элемента:
-
 ;
; -
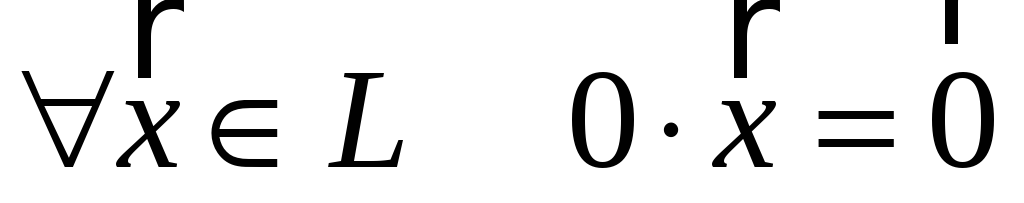 ;
;
d) определение операции разности векторов линейного пространства:
![]() .
.
Приведем некоторые примеры линейных пространств:
-
множества коллинеарных, компланарных и всех свободных геометрических векторов −
 ,
,
 и
и
 ,
соответственно;
,
соответственно; -
множество многочленов степени не выше
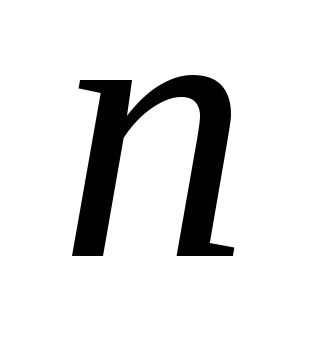 −
−
 ;
; -
множество функций, непрерывных на заданном отрезке
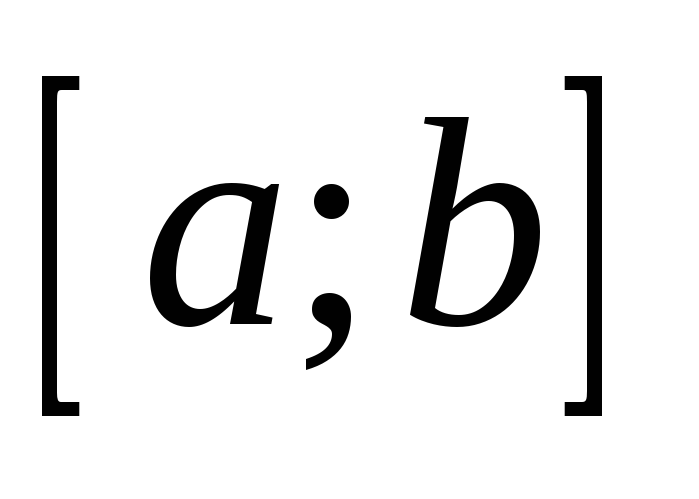 −
−
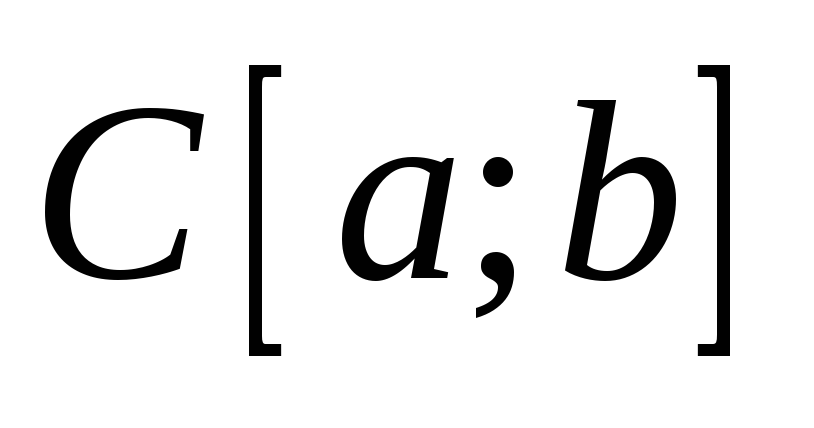 .
.
§3.2. Линейная зависимость и линейная независимость
векторов линейного пространства
3.2.1.
Определение.
Линейной
комбинацией
векторов
![]() с коэффициентами
с коэффициентами
![]() называется вектор
называется вектор
![]() .
Здесь
.
Здесь
![]() − заданные числа.
− заданные числа.![]()
Замечание.
Если все коэффициенты линейной комбинации
равны нулю
![]() ,
то она называется тривиальной.
Если же среди коэффициентов линейной
комбинации найдется хотя бы один отличный
от нуля, то она называется нетривиальной.
,
то она называется тривиальной.
Если же среди коэффициентов линейной
комбинации найдется хотя бы один отличный
от нуля, то она называется нетривиальной.
3.2.2.
Определение.
Система векторов
![]() называется линейно
зависимой,
если существует их нетривиальная
линейная комбинация, равная нулевому
вектору, т.е.
называется линейно
зависимой,
если существует их нетривиальная
линейная комбинация, равная нулевому
вектору, т.е.
![]()
3.2.3.
Определение.
Система векторов
![]() называется линейно
независимой,
если только их тривиальная линейная
комбинация равна нулевому вектору, т.е.
называется линейно
независимой,
если только их тривиальная линейная
комбинация равна нулевому вектору, т.е.
![]()
3.2.4. Теорема. (Критерий линейной зависимости системы векторов линейного пространства)
Для того, чтобы система векторов линейного пространства была линейно зависима, необходимо и достаточно, чтобы один из векторов являлся линейной комбинацией остальных векторов системы.
Доказательство: полностью аналогично доказательству соответствующей теоремы для свободных геометрических векторов 1.4.5.
3.2.5. Свойства линейно зависимых и линейно независимых систем векторов линейного пространства.
-
Всякая система векторов линейного пространства, включающая нулевой вектор, является линейно зависимой.
-
Система векторов линейного пространства, содержащая линейно зависимую подсистему, является линейно зависимой.
-
Всякая подсистема линейно независимой системы векторов линейного пространства является линейной независимой.
Доказательство приведенных свойств полностью аналогично доказательствам соответствующих теорем 1.4.6.1-1.4.6.3 для свободных геометрических векторов.
3.2.6. Определение. Базисом линейного пространства называется упорядоченная совокупность линейно независимых векторов, таких, что всякий вектор линейного пространства может быть представлен в виде линейной комбинации этой совокупности векторов.
3.2.7. Определение. Представление вектора в виде линейной комбинации векторов базиса называется его разложением по данному базису.
3.2.8. Определение. Линейное пространство называется n-мерным, если число векторов в его произвольном базисе равно n. При этом число n называется размерностью линейного пространства.
Примеры:
![]()
3.2.9. Теорема. (О разложении вектора линейного пространства по базису)
Всякий вектор конечномерного линейного пространства может быть разложен по его произвольному базису, притом единственным образом.
Доказательство полностью опирается на приведенное определение 3.2.6 и доказательство аналогичной теоремы 1.5.5 для геометрических векторов.
3.2.10. Определение. Коэффициенты разложения вектора конечномерного линейного пространства по некоторому базису называются координатами вектора в этом базисе.
3.2.11. Теорема. (Операции с векторами линейного пространства в координатной форме)
При сложении двух векторов линейного пространства их координаты в произвольном базисе складываются, а при умножении вектора на число его координаты умножаются на это же число.
Доказательство полностью аналогично приведенному в теореме 1.5.6 для геометрических векторов.
§3.3. Подпространство линейного пространства
3.3.1. Определение. Подмножество M линейного пространства L называется подпространством исходного линейного пространства L, если оно является замкнутым относительно введенных операций сложения векторов и умножения их на число, т.е.
-
 ;
; -

Примеры:
![]() является
подпространством
является
подпространством
![]() ;
;
![]() является подпространством
является подпространством
![]() .
.
Замечание. Можно показать, что всякое подпространство линейного пространства в свою очередь является линейным пространством относительно введенных операций сложения векторов и их умножения на число.
3.3.2.
Определение.
Линейной
оболочкой
векторов
![]() линейного пространства называется
совокупность всевозможных линейных
комбинаций этих векторов:
линейного пространства называется
совокупность всевозможных линейных
комбинаций этих векторов:
![]() .
.
Замечание.
Легко проверить, что линейная оболочка
векторов
![]() является подпространством линейного
пространства. С другой стороны ясно,
что всякое подпространство, содержащее
элементы вида
является подпространством линейного
пространства. С другой стороны ясно,
что всякое подпространство, содержащее
элементы вида
![]() ,
должно содержать и векторы
,
должно содержать и векторы
![]() .
Таким образом, можно сделать вывод о
том, что линейная оболочка векторов
.
Таким образом, можно сделать вывод о
том, что линейная оболочка векторов
![]() является наименьшим подпространством
исходного линейного пространства,
содержащим векторы
является наименьшим подпространством
исходного линейного пространства,
содержащим векторы
![]() .
.
