§2.6. Взаимное расположение прямых и плоскостей в пространстве.

2.6.1. Взаимное расположение прямой, заданной общими уравнениями, и плоскости.

В пространстве прямая может

а) пересекать плоскость;

б) быть параллельной плоскости;

в) лежать в плоскости.

Пусть плоскость задана общим уравнением

,

а прямая задана общими уравнениями

Тогда взаимное расположение прямой и плоскостью определяется системой трех линейных уравнений относительно трех неизвестных:

(2.18)

Если система уравнений (2.18) имеет единственное решение, то прямая и плоскость пересекаются; если у системы нет решений, то прямая параллельная плоскости; и, наконец, если у системы бесконечное множество решений, то прямая лежит в плоскости.

2.6.2. Взаимное расположение прямой, заданной параметрическими уравнениями, и плоскости.

Пусть плоскость задана общим уравнением

,

а прямая задана параметрическими уравнениями

Подставим параметрические уравнения в уравнение плоскости. Получим линейное уравнение относительно параметра t

. (2.19)

Если выполняется условие , то уравнение (2.19) разрешимо относительно параметраt

, (2.20)

и координаты точки пересечения прямой и плоскости имеют вид

где определяется из (2.20).

Если , при этом,то уравнение (2.19) не разрешимо относительно параметра t, то есть прямая не пересекает плоскость. Таким образом, условие параллельности прямой и плоскости имеет вид

Если же оба коэффициента уравнения (2.19) равны нулю, то оно справедливо для любого значения параметра, то есть имеет бесконечное множество решений. Следовательно, прямая лежит в плоскости при условии

2.6.3. Угол между прямой и плоскостью.

Уголмежду прямой и плоскостью (т.е. угол между прямой и ее проекцией на плоскость) связан с угломмежду прямой и нормалью к плоскости соотношением, поэтому

.

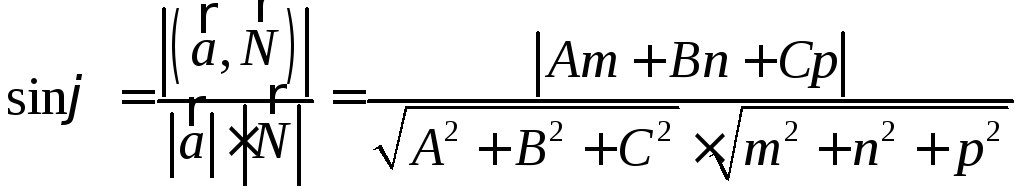В частности, если векторы и коллинеарны, то есть

,

то прямая перпендикулярна плоскости.

2.6.4. Взаимное расположение двух прямых.

Две прямые в пространстве могут

а) быть компланарными, в том числе пересекаться, быть параллельными или совпадать;

б) не быть компланарными, то есть скрещиваться.

Пусть две прямые заданы своими каноническими уравнениями

,.

Прямые компланарны тогда, и только тогда, когда компланарны векторы , и . Таким образом,условие компланарности прямых l₁ и l₂ имеет вид

. (2.21)

Если при этом векторы , коллинеарны, т.е. , то прямые параллельны. Если, дополнительно, векторколлинеарен направляющим векторам, то прямые совпадают.

Если условие компланарности выполняется, но направляющие векторы неколлинеарны, то прямые пересекаются. Чтобы найти точку пересечения, надо решить систему уравнений

В этой системе три неизвестных (координаты точки пересечения х, у, z) и четыре уравнения, однако, если выполняются условия компланарности прямых и неколлинеарности направляющих векторов, она имеет единственное решение.

2.6.5. Расстояние от точки до прямой в пространстве.

Найдем расстояние от некоторой точкидо прямойl, имеющей направляющий вектор и проходящей через точку. Очевидно, искомое расстояние будет являться высотой параллелограмма, построенного на векторахи. Используя геометрический смысл векторного произведения, окончательно получаем:

. (2.22)

Чтобы найти расстояние между параллельными прямыми, нужно найти расстояние от произвольной точки первой прямой до второй прямой.

2.6.6. Расстояние между скрещивающимися прямыми.

Найдем расстояние между скрещивающимися прямыми, заданными своими каноническими уравнениями

Так как прямые l₁ и l₂ скрещиваются, то векторы , и некомпланарны. Очевидно, что если построить параллелепипед на векторах , и (Рис. 2.17), то искомое расстояние будет равно высоте параллелепипеда. С учетом свойств смешанного и векторного произведений получим

(2.23)

Лекция 7.