Надежность технических систем и техногенный риск. Часть 1. Надежность

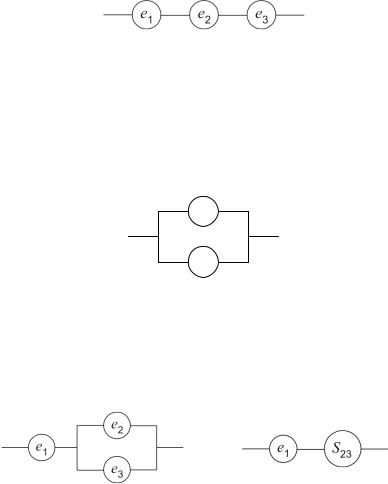
На рис. 8.1 в виде структурной схемы представлена система из трех элементов, не содержащая резервных элементов. Элементы в ней соединены последовательно. Такое соединение элементов часто называют основным. Система работоспособна только в том случае, когда все ее элементы работоспособны.

Рис. 8.1. Пример системы без резервных элементов

На рис. 8.2 представлен простейший пример структурной схемы резервированной системы, состоящей из двух параллельно соединенных элементов. Каждый из элементов служит для другого резервным. Единственное условие отказа такой системы – это отказ обоих элементов.

Рис. 8.2. Простейшая система с резервированием

Более сложная структурная схема системы с раздельным (поэлементным) резервированием изображена на рис. 8.3, а. Здесь только один из элементов имеет резервный.

Рис. 8.3. Система с раздельным резервированием

71

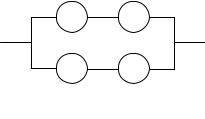
Для расчета надежности системы, изображенной на рис. 8.3, а, можно использовать прием агрегирования части элементов в виде подсистемы с более простой структурой: можно считать, что элементы e2 и e3, соединенные параллельно, образуют подсистему S23. Тогда в основная система оказывается состоящей из двух последовательно соединенных элемента e1 и подсистемы S23 (рис. 8.3, б). Далее расчет надежности можно выполнить последовательно, начиная с оценки надежности выделенной подсистемы S23.

На рис. 8.4. представлена резервированная система, в которой использовано общее резервирование.

Рис. 8.4. Система с общим резервированием

На приведенных выше структурных схемах 8.1–8.4 примерах все резервные элементы подключены постоянно, т.е. резервные элементы находятся в нагруженном состоянии.

Основной недостаток структурных схем – неполная информация об изображаемой системе: неясно, является ли система ремонтируемой, равноценны ли с точки зрения надежности входящие в нее элементы и т.п. Поэтому структурные схемы систем требуют дополнительного описания их работоспособности.

8.2.Надежность систем, не имеющих резервных элементов

Вэтом подразделе приведены оценки надежности систем без резервирования с независимыми элементами, работающими до первого отказа, а также оценки надежности восстанавливаемых систем.

72

8.2.1. Расчет надежности системы с независимыми элементами, работающей до первого отказа

В качестве основной характеристики безотказности невосстанавливаемой системы выступает функция ее надежности, представляющая собой вероятность P(t) безотказной работы в течение времени t.

Если система состоит из двух независимых последовательно соединенных элементов с вероятностями P1(t) и P2(t) безотказной работы за время t, то вероятность P(t) безотказной работы такой системы в течение времени t в силу независимости элементов равна произведению вероятностей P1(t) и P2:

P(t) = P1(t) · P2(t).

Если же система состоит из n независимых элементов и вероятность безотказной работы i-го элемента в течение времени t равна Pi(t), то вероятность P(t) безотказной работы системы в течение

Если функции надежности составляющих систему элементов подчиняются экспоненциальному закону распределения с постоянными интенсивностями λi отказов:

Pi(t) = exp[−λi t], t ≥ 0,

то функция надежности системы оценивается по следующей формуле:

Математическое ожидание MT времени T безотказной работы для случая экспоненциального распределения вычисляется по следующей формуле:

Для систем, работающих до первого отказа, среднее время Tср жизни системы (наработка на отказ) является статистической оценкой математического ожидания MT:

Tср MT.

По результатам испытаний его можно оценить как среднюю наработку системы на отказ по следующей формуле:

где Tс – суммарная наработка системы по результатам испытаний (или эксплуатации); k – суммарное число отказов, зарегистрированное в процессе этих испытаний.

8.2.2.Оценка ремонтопригодности восстанавливаемой системы

Вкачестве основной характеристики ремонтопригодности восстанавливаемой системы выступает математическое ожидание

M(Tв) случайной величины Tв – времени восстановления, которое можно найти по следующей формуле:

где Fв(t) – интегральная функция распределения времени восстановления системы.

Оценка ремонтопригодности восстанавливаемых систем с последовательным соединением элементов часто строится на предположении о том, что поток восстановлений является простейшим (пуассоновским) с постоянной интенсивностью параметра µ этого потока. В этом случае после подстановки функции распределения Пуассона в формулу (8.5) и вычисления соответствующего интеграла получим следующую формулу для математического ожидания MTв времени Tв восстановления такой системы:

74

Если же восстанавливаемая система состоит из n последовательно соединенных независимых элементов с разными интенсивностями восстановления µi (i = 1, 2, …, n), то математическое ожидание временивосстановлениясистемыможнооценитьпоформуле:

∑µi

i−1

Несмещенной статистической оценкой величины MTв служит среднее время Tв ср восстановления системы, которое можно вычислить по результатам испытаний или эксплуатации следующим образом:

где ni – это число отказов i-го элемента; tiв – время восстановления i- го отказа.

Следует иметь в виду, что статистическая оценка (8.7) является случайной величиной, значения которой зависят от условий испытаний и объема опытных (выборочных) данных.

8.2.3. Надежность восстанавливаемой системы без резервных элементов

Важнейшие критерии надежности восстанавливаемых объектов – это функция Kготов(t) и коэффициент Kготов готовности объекта к работе в произвольный момент времени t. В гл. 6 были даны определения коэффициентов готовности и приведены формулы для их вычисления для случая простейших потоков отказов и восстановлений (см. формулы (6.6) и (6.7)). В частности, этими формулами можно пользоваться для оценки надежности восстанавливаемой системы, рассматриваемой как один элемент.

75

В общем случае оценку показателей надежности восстанавливаемой системы, состоящей из N последовательно соединенных элементов, можно выполнить с помощью опытных данных следующим образом.

Tо.ср – средняя наработка системы на отказ и Tв – среднее время восстановления системы оцениваются по формулам:

через Ti – среднее время между отказами (наработка на отказ) i-го элемента и Tв.i – среднее время восстановления i-го элемента.

С учетом формул (8.9) и (8.10) коэффициент готовности Кготов нерезервированной восстанавливаемой системы оценивается следующим образом:

Коэффициент готовности является усредненной характеристикой надежности восстанавливаемой системы, оценивающей вероятность того, что система окажется работоспособной в произвольный момент времени. При этом из рассмотрения исключаются периоды плановой остановки системы, в течение которых ее использование по назначению не предусмотрено.

Кроме коэффициента готовности Kготов для оценки надежности восстанавливаемой системы используют также коэффициент Kоп. г оперативной готовности системы, который дополнительно учитывает вероятность P(tо, t1) безотказной работы системы на промежутке (tо, t1):

76

Коэффициент Kоп.г оперативной готовности оценивает вероятность того, что в произвольный момент времени tо (за исключением планируемых периодов, в течение которых использование системы по назначению не предусматривается) эта система окажется работоспособной и, кроме того, будет безотказно работать вплоть до момента t1 прекращения ее использования по назначению.

8.3.Повышение надежности невосстанавливаемых систем

спомощью резервирования

Пусть система состоит только лишь из двух параллельно соединенных элементов с вероятностями q1 и q2 отказов за время t. Тогда вероятности безотказной работы первого и второго элемента за время t будут равны соответственно p1 = 1 – q2q1 и p2 = 1 – q2. В такой системе каждый из элементов является для другого резервным. Поэтому система окажется неработоспособной только в том случае, когда оба элемента выйдут из строя. Вероятность этого события равна произведению вероятностями q1q2 вероятностей отказов, а вероятность P(t) того, что в течение времени система работоспособна, вычисляется по формуле:

Если система состоит из N независимых, параллельно соединенных элементов и pi (i = 1, 2, …, N) – вероятность безотказной работы i-го элемента в течение времени t, тогда вероятность безотказной работы такой системы можно вычислить по аналогичной формуле:

В частности, если отказы каждого из N элементов такой системы распределены экспоненциально, причем интенсивности отказов одинаковы и равны λ, то вероятность безотказной работы за время t вычисляется по формуле:

77

а среднее время безотказной работы такой системы Tср (средняя наработка системы на отказ) определится по формуле:

Замечание. Формула (8.1) пригодна для расчета времени P(t) безотказной работы системы, в которой нет резервных элементов, а все элементы независимы и соединены последовательно. Формула (8.14) используется для вычисления времени P(t) в случае, когда все N элементов соединены параллельно, т.е. для любого из отдельных элементов системы подсистема из оставшихся N – 1 элементов является резервной. В совокупности этими формулами можно воспользоваться и для оценки времени безотказной работы некоторых более сложных систем, в которых элементы соединены как последовательно, так и параллельно. С этой целью можно составить структурную схему соединения элементов, выделяя в ней отдельные подсистемы.

Пример 8.1. Пусть к системе S1 из двух последовательно соединенных элементов e1 и e2 с вероятностями безотказной работы p1

иp2 соответственно в качестве резервного к элементу e2 добавлен (параллельно подсоединен к нему) элемент e3 с вероятностью безотказной работы p3. Тогда параллельно соединенные элементы e2

иe3 образуют подсистему S23, время P23(t) безотказной работы которой можно вычислить по формуле (8.13):

P23 (t) = 1 – q2q3 = 1 – [(1 – p2)(1 – p3)].

Элемент e1 оказывается соединенным с подсистемой S23 последовательно. Поэтому вероятность P(t) безотказной работы системы, составленной из всех трех элементов, в этом случае можно вычислить по формуле (8.1):

P(t) = p1 · P23 (t) = p1 · [1 – q2 q3 ] = p1 · [1 – [(1 – p2)(1 – p3)]] = = p1 p2 + p1 p3 (1 – p2) > p1 p2.

78

Поскольку до добавления резервного элемента вероятность безотказной работы исходной системы из двух элементов e1 и e2, очевидно, была равна произведению p1p2, то полученное неравенство показывает, что надежность системы увеличилась при добавлении к ней резервного элемента.

Пример 8.2. Пусть на этот раз для системы S1 из двух последовательно соединенных элементов e1 и e2 выполнено общее резервирование с помощью элемента e3. Тогда операцию агрегирования можно применить к подсистеме S12, вероятность P12(t) безотказной работы которой находим по формуле (8.1):

P12(t) = p1 · p2.

В полученной системе из трех элементов подсистема S12 и элемент e3 оказываются соединенными параллельно. Поэтому вероятность P(t) безотказной работы этой системы вычисляется по формуле (8.14):

P(t) = 1 – q12q3 = 1 – [(1 – p12) · (1 – p3)] = 1 – [(1 – p1 · p2)(1 – p3)].

После несложных выкладок можно снова убедиться, что надежность системы после операции резервирования возросла.

Наиболее просто вычисляется вероятность работы системы с однородными независимыми элементами, содержащими резервные элементы, так как в этом случае можно напрямую воспользоваться формулой Бернулли.

Пример 8.3. Рассмотрим систему с независимыми однородными элементами, содержащую n основных элементов и k резервных. Пусть для любого из элементов вероятность безотказной работы за время t равна p (соответственно, в этом случае вероятность отказа элемента q = 1 − p). Пусть резервные элементы находятся в нагруженном состоянии и система отказывает, если число работоспособных элементов в ней оказывается меньше n.

Вероятность P(t) работоспособного состояния такой системы – это вероятность того, что число отказов за время t не превышает n. Она может быть вычислена как вероятность суммы несовместных (непересекающихся) событий с помощью формулы Бернулли (5.1):

79

Например, если в такой системе три основных элемента и один резервный, то по формуле (8.17) получим, что вероятность P(t) безотказной работы такой системы равна вероятности того, что число отказавших элементов − не более одного, при этом

P(t) = C41 (1 − q)p3 + C40 p4 = 4qp3 + p4.

Отметим, что этот результат с точностью до обозначений совпадает с результатом, полученным в примере 7.3.1 (в примере 7.3.1 через p была обозначена вероятность отказа элемента). Так как вероятность q > 0, а вычисленную вероятность работоспособности системы можно представить в виде:

P(t) = 4qp3 + p4 = p3(4q + p) = p3(1 + 3q) > p3,

то последнее неравенство означает, что надежность исходной системы (без резервного элемента) меньше.

В инженерной практике резервирование как способ повышения надежности систем используется давно: например, сдвоенные колеса грузовиков и самолетных шасси – общеизвестный способ сохранить способность транспортного средства нести нагрузку, если одна из шин лопнет. В приведенном примере реализуется горячее (нагруженное) резервирование. Холодное резервирование используется, например, в детских велосипедах: если двухколесный велосипед теряет равновесие и заваливается набок, то от падения велосипед (и, следовательно, ребенка) защищает то из двух резервных боковых колес, на которое в этом случае переходит часть нагрузки (резервные колеса не касаются поверхности дороги в состоянии равновесия). Таким образом, ребенок пользуется резервными колесами до тех пор, пока не научится держать равновесие при езде на двух колесах.

Отметим, что надежность системы еще более увеличивается, если используется резервирование с восстановлением, которое выходит за рамки нашего пособия.

80