Методические указания к решению задач олимпиады по сопротивлению материалов (120

Рис. 23

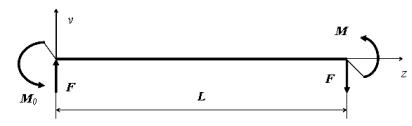
Рис. 24

Решение. Мысленно разрежем трос и заменим его действие на балку (рис. 23) силой N.

Это равносильно действию внецентренной сжимающей нагрузки, отчего возникает дополнительный изгибающий момент М (рис. 24). Значение силы N пропорционально удлинению троса, которое, в свою очередь, зависит от поворота торца балки ϑ:

гой линии балки.

Момент в заделке М0 найдем из условия равновесия балки:

M0 = FL −M .

Универсальное уравнение имеет вид

EIxv = F z63 −M0 z22 ;

21

Рис. 25

Задача 9. Для увеличения прочности и жесткости полки, выполненной в виде шарнирно закрепленной балки, предложено два варианта расположения подкрепляющих ребер (рис. 26).

Рассчитать, на сколько увеличится прочность и жесткость балки в том и другом варианте.

Дано: L, B, H , E, p.

22

Рис. 26

Решение. Для сравнения прочности и жесткости двух вариантов подкрепления полок следует вычислить геометрические характеристики подкрепленных полок для двух вариантов.

Рис. 27

Определим момент инерции поперечного сечения подкрепляющего ребра (рис. 27).

Считая, что h H, получим:

23

Площадь поперечного сечения подкрепляющего ребра

A = 4 H6 B5 = 152 HB = 2B2.

Далее найдем положение нейтральной линии подкрепленной полки в первом варианте (рис. 28).

Рис. 28

Момент инерции поперечного сечения всей полки

=15,0877B4 ,

а момент сопротивления изгибу

Для второго варианта подкрепления нейтральная линия проходит через центр тяжести неподкрепленной полки, и момент инерции вычисляется проще:

24

момент сопротивления

Таким образом, во втором варианте подкрепления жесткость больше примерно на 17 %, чем в первом, а прочность — всего на

2,8 %.

С конструктивной точки зрения первый вариант наиболее предпочтителен. Сравнение прочности и жесткости подкрепленной и неподкрепленной полок показывает, что подкрепление увеличивает прочность почти в 2,3 раза, а жесткость — в 12 раз, при этом масса подкрепленной полки возрастает всего на 27 %.

Задача 10. Построить эпюры окружных и меридиональных напряжений для конической оболочки (рис. 29), заполненной внутри жидкостью с плотностью ρ.

Дано: H , α, h, ρ.

Рис. 29

25

Рис. 30

Решение. Окружной и меридиональный радиус оболочки выразим через координату z, отсчитываемую от вершины оболочки вдоль оси конуса (рис. 30):

Из уравнения Лапласа получим:

Окончательно имеем:

σt = ρhgcostgαα z2 .

Для вычисления меридиональных напряжений запишем условие равновесия отсеченной части оболочки (рис. 31):

ρgzπr2 = 13 πr2 zρg +σm 2πrhcos α,

откуда

σm = 13 ρhgcostg αα z2 .

Построим эпюры (рис. 32).

26

Рис. 31

Рис. 32

27

Учебное издание

Горбатовский Александр Александрович Котов Александр Иванович

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ОЛИМПИАДЫ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ

Редактор С.А. Серебрякова Корректор Е.К. Кошелева

Компьютерная верстка С.А. Серебряковой

Подписано в печать 17.03.2010. Формат 60×84/16. Усл. печ. л. 1,63. Тираж 100 экз. Изд. № 131. Заказ

Издательство МГТУ им. Н.Э. Баумана. Типография МГТУ им. Н.Э. Баумана. 105005, Москва, 2-я Бауманская ул., 5.

28