Методические указания к решению задач олимпиады по сопротивлению материалов (120

Рис. 11

Вид эпюры изгибающих моментов M x от силы F, начиная с

момента размыкания контактов и в процессе дальнейшего нагружения, представлен на рис. 12.

Рис. 12

11

Следовательно, в момент размыкания контактов точка B опускается (см. рис. 12) на величину

Чтобы обеспечить надежное размыкание контактов (см. условие задачи), следует приложить дополнительно силу (F − FAB ), определяемую из равенства

Задача 5. Определить работу силы F при наибольшем относительном угле ϑOB поворота сечений O и B (рис. 13) для a = var

(0 ≤ a ≤l).

Найти диапазон изменения параметра a, соответствующий ог-

Рис. 13

12

Рис. 14

Решение. Горизонтальная пружина (коэффициент жесткости Z0) не работает. Силы, действующие на пружины с жесткостями Z1 и Z2 (рис. 14), можно найти из уравнений равновесия (суммы моментов всех сил, действующихна балкуотносительноточек O и B).

Относительный угол поворота ϑOB не зависит от деформации

пружин, но определяется изгибной деформацией балки и согласно рис. 14 составляет

Очевидно, что наибольшее значение угла ϑOB принимает при a = 2l , т. е.

13

1 Fl2

(ϑOB )max = 8 EIx .

При значении a = 12 l (рис. 15) перемещение точки приложения

силы F, определяемое методом Мора с учетом сжатия вертикальных пружин, равно

Рис. 15

14

Работа, совершаемая силой F в этом случае, определяется величиной

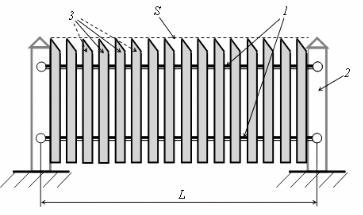
Задача 6. Лаги 1 деревянного забора (рис. 16), имеющие изгибную жесткость поперечного сечения EIx каждая, шарнирно

закрепляют на столбах 2. Затем к ним прибивают штакетины 3. Обосновать теоретически, как следует прибивать штакетины (с

очень малыми просветами между ними), чтобы после окончания работ верхний край S забора был горизонтален.

Дано: L — длина пролета, m — масса штакетины, n — число штакетин в пролете, E, Ix .

Рис. 16

15

Рис. 17

Решение. Поскольку просветы между штакетинами не велики,

весовую нагрузку q = mgnL на лаги можно считать равномерно

распределенной (g — ускорение свободного падения). Предполагая совместную работу верхней и нижней лаг, реше-

ние поставленной проблемы можно свести к поиску кривой прогибов v(z) шарнирно опертой балки (рис. 17) с изгибной жесткостью

2EIx и равномерно распределенной нагрузкой q.

Дифференциальное уравнение упругой линии рассматриваемой балки имеет вид

После двукратного интегрирования находим:

где C1 и C2 — постоянные интегрирования, определяемые из граничных условий. В данном случае при z = 0 и z = L имеем v = 0.

Уравнение упругой линии балки в этом случае принимает вид

16

Перейдя к безразмерной координате ζ = Lz , запишем

Теоретические рекомендации состоят в том, что каждую штакетину следует прибивать с превышением v(zi ), где zi — абсцисса конкретной штакетины. Например, штакетина в самом центре про-

Рис. 18

Задача 7. В конструкции, показанной на рис. 18, сечение с мо-

жет повернуться на угол ϕс = ML .

GI p

17

Вычислить работу, совершаемую моментами.

Дано: М, L, Ip, G.

Решение. Раскрыв статическую неопределимость, построим эпюры (рис. 19) крутящих моментов и углов поворота:

Далее найдем значение внешнего момента М0, при котором закрывается зазор:

Рис. 19

18

Рис. 20

Построим эпюры крутящих моментов и углов поворота в момент закрытия зазора (рис. 20).

Для вычисления работы, совершаемой каждым из моментов, построим графики (рис. 21) зависимостей углов поворота сечений b и c от внешних моментов.

Работа, совершаемая каждым из моментов, равна площади фигуры под графиком зависимости момента от угла поворота. При этом следует обратить внимание на то, что до закрытия зазора момент М совершал отрицательную работу, поскольку направления момента и угла закручивания сечения b были противоположны.

В результате вычисления находим:

19

Рис. 21

Задача 8. Консольная балка (рис. 22) нагружена силой F. Вдоль верхней части балки протянут идеально гибкий трос, который крепится с одной стороны к заделке, а с другой — к жесткой крышке на конце балки. Найти прогиб конца балки (расстояние с считать малым).

Дано: E — модуль упругости материала балки, EA — жесткость поперечного сечения троса, F, L, B, H.

Рис. 22

20