Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Владимирский государственный университет им. Столетовых

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Линейная алгебра и аналитическая геометрия. Рабочая тетрадь 6 «Векторная алгебра» (90

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

505.6 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Задача 15

Найдите косинус угла, образованного векторами:

а)

(2; 4;4)

и b ( 3;2;6); б)

(2; 4;4)

и b (4; 2; 4).

Решение.

а)

(2; 4;4)

( 3;2;6)

По формуле скалярного произведения двух векторов выразим косинус угла

a b

между двумя векторами a и b: a b

a, b

cos

Найдем скалярное произведение векторов

и их модули.

3 2 2 ( 4) 6 4 6 8 24 10,

22 ( 4)2 42

( 3)2 4 36

4 16 16

9 4 36

a, b

т.е. cos

б)

(2; 4;4)

(4; 2; 4)

_____________________________________________________________

		5
	a, b	5		a, b	0

Ответ. а) cos			; б) cos
		21
		21

Задача 16

Дан треугольник ABC.. Определите внутренний угол при вершинеB,если даны координаты вершин:

а) A ( 1; 2; 4), B( 4; 2; 0), C(3; 2;1);

б) A (1; 1; 1), B(2;1;1), C(3; 2;1).

Решение.

а) A ( 1; 2; 4), B( 4; 2; 0), C(3; 2;1)

Найдем координаты векторов: BA (3;0;4), BC (7;0;1). Выпишем формулу

и подставим в нее значение.

cos B		BA			BC				3 7 0		0 4 1


		BA			BC			32 02 42			72 02 12
	21 4					25					25	1		B 45
														B 45
	9 16			49 1			25			50 5 5 2			2
б) A (1; 1;			1), B(2;1;1),						C(3; 2;1)

__________________________________________________________________

___________________________________________________________________

Ответ. а) B 45 ; б) B 135

Задача 17

Найти координаты вектора c , коллинеарный вектору a , образующий

острый угол с заданной осью, c 50, если:

а) a (6; 8; 7,5), с осью OZ; б) a (2; 3; 6), с осью OX.

Решение.

c (x; y;

z),

(6; 8; 7,5).

x 6t,

t y 8t,

7,5

6 8

z 7,5t.

c 50 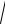x2 y2 z2 50,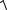 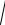6t 2 8t 2 7,5t 2 50,

36t2 64t2			225		t2		50			144t2	256t2	225t2	50,
36t2 64t2					t2		50				4		50,
				4							4

	625t2			25	t			t	4.
		50				50
4		50		2		50
4				2

t	4,
t	4,		c1 (24; 32; 30),							c2	( 24;32;30),
1	4,		c1 (24; 32; 30),							c2	( 24;32;30),
t2	4,
					30		3

		c , k						0		c , k			90 ,

cos
		1			50		5			1
					50		5
				30		3

							0					90		c ( 24; 32; 30).
cos c2, k				50		5	0		c2, k			90		c ( 24; 32; 30).
				50		5

б) a (2; 3; 6), с осью OX

__________________________________________________________________

Ответ: а)	c	24; 32; 30 , б)	c	100		150		300
					;		;
				7		7		7

Задание 18

Найдите координаты вектора c , зная, что:

а) вектор c перпендикулярен векторам a (2;3; 1) и b (1; 2;3) и

удовлетворяет условию c 2i j k 6;

б) вектор c перпендикулярен оси OZ и удовлетворяет условию

c 3i j 5k 9 и c i 2 j 3k 4.

Решение.

а) c (x;y;z), a (2;3; 1), b (1; 2;3).

c a 2x 3y z 0, c b x 2y 3z 0 и 2x y z 6.

x 2y 3z 0,

2x 3y z 0,Решим систему линейных уравнений.

2x y z 6.


	1		2	3		0			2	3
	2		3	1	14, x	0			3	1		42,
	2		1	1			6		1	1
		1	0	3	42, z			1	2	0	42,		x 3,	y 3, z 3.
		1	0	3				1	2	0
y		2	0	1				2	3	0
		2	6	1				2	1	6

б) c (x;y;z)

__________________________________________________________________

Ответ. а) c 3; 3; 3 ; б) c 2; 3;0

Задание 19

Найдите координаты вектора d , удовлетворяющий условиям:

а) d

d b 11; d

20,

(2; 1;3), b (1; 3;2) и

(3;2; 4);

б)

11;

(1;2;4),

(5; 2;3) и

( 7;8;2).

Решение.

а) Найдем координаты вектора d (x; y;z)используя условия:

d a 5; d b 11; d c 20:

2x y 3z 5,
	x 3y 2z 11,
	x 3y 2z 11,
				20.
3x 2y 4z				20.
		2		1	3	39,			5		1		3		78,
		2		1	3				5		1		3
		1		3	2			x	11 3				2
		3		2	4					20		2	4
			2	5	3		117, z		2		1		5	78,x 2;		y 3;	z 2.
			2	5	3				2		1		5
	y		1	11	2				1	3		11
			3	20	4				3		2		20

б) Найдем координаты вектора d (x; y;z)используя условия:

d a 11; d b 9; d c 5:

__________________________________________________________________

Ответ. а) 2; 3; 2 ; б) 1;1;2

Задание 20

Даны координаты векторов

j 3k и b i 3 j 2k . Найдите:

а)

, 2

;

б) 2

, 2

Решение.

а)

, 2

a (2;1; 3), b (1; 3; 2). Найдем векторное произведение векторов

		i	j	k
a	b	2	1 3		2	i	3	j	6	k	(	k	9	i	4	j	) 11	i	j	7	k	,
		1	3	2

2a 3b b 4a 2a b 8a a 3b b 12b a

2a b 12a b 14a b 14(11i j 7k) 154i 14j 98k .

б) 2a b b ____________________________________________________________

_____________________________________________________________________________,

2a b 2a b _______________________________________________

_______________________________________________________________.

Ответ. а) 11; 1; 7 ,

154; 14; 98 ; б) 22; 2; 14 , 44; 4; 28

Задание 21

Найдите площадь треугольника ABC с вершинами в точках:

а)A (4; 2; 6), B (2;8; 4), C (6; 2; 2); б) A (1;2;0), B (3;2;1), C ( 2;1;2).

Решение.

а)A (4; 2; 6), B (2;8; 4), C (6; 2; 2)

Используя геометрический смысл векторного произведения двух векторов

найдем площадь треугольника: S 1 BA BC .

Найдем координаты векторов: BA (2; 10;2), BC (4; 10; 6).

Сначала вычислим векторное произведение двух векторов BA и BC:

		i	j	k	i	j	k
BA	BC	2	10	2	41	5	1
		4	10	6	2	5	3

415i 5k 2j 10k 5i 3j 4 20i 5j 5k

80i 20j 20k BA BC (80; 20; 20).

	1				1			1
S						802 202 202				30		ед2.
		BA	BC						6400 400 400		2
		BA	BC						6400 400 400		2
2				2			2
2				2			2

б) A (1;2;0), B (3;2;1), C ( 2;1;2)

_____________________________________________________________

Ответ. а)SABC 30		(ед2); б) SABC		3		(ед2)
	2				6

			2

Задание 22

Найдите площадь треугольника, построенного на векторах a и b:

а)a 3i 2 j k и b i j 2k ; б) a i 2 j 5k и b 5 j 7k .

Решение.

а)a 3i 2 j k и b i j 2k

Найдем площадь треугольника, используя геометрический смысл векторного

произведения двух векторов																		и			:		(3;2;1),				1; 1;2 .					S		1			.
																	a			b		a				b								1	a	b
																	a			b		a				b									a	b
																															2
																															2
Найдем векторное произведение двух векторов																														и		:
Найдем векторное произведение двух векторов																													a	и	b	:
							2		1			1		3		3			2
							2		1			1		3		3			2
a b											;				;							, a b 5; 5; 5 .
							1		2			2		1		1		1
							1		2			2		1		1		1
		1							1													1						1			5
													2			2			2
	S			a b									2			2			2														3.
										5				5				5							25 25 25					75
										5				5				5							25 25 25					75
		2							2													2		2							2
		2							2													2		2							2
			5					ед2 .
	S		5			3
	S				2
					2

б) a i 2 j 5k и b 5 j 7k

_____________________________________________________________

Ответ. а)Sтреуг	5			1		ед2)
			3(ед2); б) Sтреуг		195(

2		2

Задание 23

Найдите площадь параллелограмма, построенного на векторах a и b :

																				3
а)	a	3	p	2	q	,		2	p	q	,	q	4,	p	3, (	p	,	q	)		;
							b
							b													4
																				4


б)	a	2	p	5	q	,	b		4		p	3			q		,		q	2,			p	5, (			p	,	q	)			.
б)	a	2	p	5	q	,	b		4		p	3			q		,		q	2,			p	5, (			p	,	q	)			.
																															4
Решение.																															4
Решение.
																															3
а)	a	3	p	2	q	,		b	2	p			q	,		q		4,			p	3, (			p	,	q	)			3	;
а)	a	3	p	2	q	,		b	2	p			q	,		q		4,			p	3, (			p	,	q	)				;
																															4
																															4

Используя геометрический смысл векторного произведения двух векторов найдем площадь параллелограмма: S a b .

a b 3p 2q 2p q 6p p 3p q 4q p 2q q

3p q 4q p 3q p 4q p q p.

p p 0 и q q 0

p q q p .

S						q			p			q	p		sin(			q		,^		p	) 4 3			2	6
		a	b																							2					2
		a	b																							2					2
																										2

б)	a	2		p	5		q	,		b	4		p	3		q	,		q		2,			p	5, (		p	,	q	)
б)	a	2		p	5		q	,		b	4		p	3		q	,		q		2,			p	5, (		p	,	q	)		4
																																4

____________________________________________________________

Ответ. а) S 62 (eд2); б) S 702 (eд2)

Задание 24

Найдите смешанное произведение a,b,c трех векторов a, b и c, если:

а) a 3i j k , b 5i 2 j 2k ,c i 3j k ;

б) a 4i 2 j k , b 2i 3j 4k ,c i j k .

Решение.

а) a 3i j k , b 5i 2 j 2k ,c i 3j k

Смешанным произведением трех ненулевых векторов a, b и c называется число равное векторному произведению векторов a и b(a b), а затем полученный вектор умножаем на вектор c скалярно. Найдем смешанное произведение трех векторов: a (3; 1;1), b (5; 2; 2), c (1; 3;1).

	3	1	1
abc	5	2	2	6 15 2 2 18 5 12 10 22.

	1	3	1

б) a 4i 2 j k , b 2i 3j 4k ,c i j k

____________________________________________________________

Ответ. а) abc 22; б) abc 15

Задание 25

Найдите объем параллелепипеда, построенного на векторах a, b и c,если:

а) a (4; 2;0),b ( 3;6;3), c (1;4; 5); б) a (1 2;1),b (3;2;1), c (1;0; 1).

Решение.

а) a (4; 2;0),b ( 3;6;3), c (1;4; 5)

Объем параллелепипеда, построенного на векторах a, b и c, как на ребрах,

равен модулю смешанного произведения трех векторов a, b и c: V abc .

Найдем смешанное произведение трех векторов a, b, c:

	4	2	0		2	1	0
abc	3	6	3	6	1	2	1	6( 20 1 8 5) 6( 24) 144.

	1	4	5		1	4	5

V abc 144 ед3 .

б) a (1 2;1),b (3;2;1), c (1;0; 1)

______________________________________________________________

Ответ. а)V 144 (ед3); б) V 12 (ед3)

Задание 26

Доказать, что 4 точки A,B,C,D лежат в одной плоскости, если точки имеют

следующие координаты:

а)A (1; 2; 1), B (0;1;	5), C ( 1; 2;1), D (2;1;			3);
б) A (3; 5;1), B (2; 4; 7), C (1;5;3), D (4; 4; 5).
Решение.
а)A (1; 2; 1), B (0;1;	5), C ( 1; 2;1), D (2;1;			3)
Найдем координаты векторов:			( 1; 1;6),			( 2;0;2),		(1; 1;4).
Найдем координаты векторов:		AB	( 1; 1;6),		AC	( 2;0;2),	AD	(1; 1;4).

Точки A, B, C, D лежат в одной плоскости, если три вектора AB, AC, AD -

компланарны, а по признаку компланарности трех векторов смешанное

произведение трех векторов должно быть равно 0, т.е. AB, AC, AD 0.

					1	1	6
AB	,	AC	,	AD	2	0	2	12 2 2 8 12 12 0.
					1	1	4

Точки A, B, C, D лежат в одной плоскости.

б) A (3; 5;1), B (2; 4; 7), C (1;5;3), D (4; 4; 5)

______________________________________________________________

Ответ. а), б) Точки A, B, C, D лежат в одной плоскости

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]