
Волновое уравнение (96
..pdfМосковский государственный технический университет имени Н.Э. Баумана
Ю.И. Малов, М.М. Сержантова, А.В. Чередниченко
ВОЛНОВОЕ УРАВНЕНИЕ
Методические указания к выполнению типового расчета по курсу «Уравнения математической физики»
Под редакцией Г.П. Стась
М о с к в а Издательство МГТУ им. Н.Э. Баумана
2 0 0 6
УДК 517.9 ББК 22.161.6
М18
Рецензент Л.К. Мартинсон
Малов Ю.И., Сержантова М.М., Чередниченко А.В.
М18 Волновое уравнение: Метод. указания к выполнению типового расчета по курсу «Уравнения математической физики» / Под ред. Г.П. Стась. – М.: Изд-во МГТУ им. Н.Э. Баумана. 2006. – 47 с.: ил.
Рассмотрено волновое уравнение и некоторые его частные решения в виде плоской, сферической и цилиндрической монохроматических волн. Приведены решения уравнений Лапласа и Пуассона в классе обобщенных функций с использованием функции Грина – функции источника.
Для студентов 2-го курса МГТУ им. Н.Э. Баумана, изучающих курс «Уравнения математической физики». Может быть полезна студентам старших курсов, изучающим соответствующую дисциплину.
Ил. 4. Библиогр. 5 назв.
УДК 517.9 ББК 22.161.6
© МГТУ им. Н.Э. Баумана, 2006
Предисловие
Данное пособие содержит краткое изложение теории уравнений в частных производных второго порядка эллиптического типа, а именно уравнений Лапласа, Пуассона, Гельмгольца.
Первая глава посвящена выводу волнового уравнения колебаний струны и электромагнитных колебаний. Вывод уравнения Лапласа приведен во второй главе. Также во второй и третьей главах рассмотрены решения волновых уравнений с помощью функции Грина.
Применение метода функции Грина вызвано необходимостью использования обобщенных функций, а именно дельта-функции и ее свойств [1], при решении различных задач физики, например задач электродинамики [2], в расчетах оптико-электронных систем [3] или при описании установившихся колебаний гибкой мембраны, закрепленной по контуру [4].
1.ВОЛНОВОЕ УРАВНЕНИЕ
1.1.Механическая модель волнового процесса. Уравнение колебаний струны
Струной называется натянутая нить, не сопротивляющаяся изгибу, но сопротивляющаяся растяжению. Отсутствие сопротивления изгибу математически выражается в том, что напряжения, возникающие в струне, всегда направлены по касательной к ее мгновенному профилю.
Будем рассматривать плоское движение струны, когда смеще-
ние находится в плоскости (x, u), |
а вектор смещения в каждый |
|
момент времени перпендикулярен |
оси Ox. Пусть в |
плоскости |
(x, u) струна совершает малые поперечные колебания |
около сво- |
|
его положения равновесия, совпадающего с осью Ox. Величину отклонения (смещения) струны от положения равновесия в точке x в момент времени t обозначим как u(x, t).
3
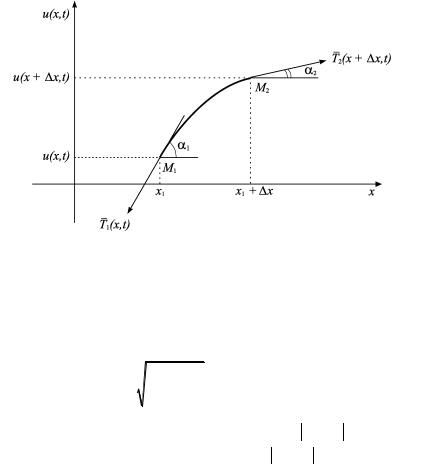
Рис. 1
Так как струна не сопротивляется изгибу, ее натяжение T (x,t) в момент t направлено по касательной к профилю струны в точке x. Любой участок струны (x1, x2 ) после отклонения от положения
равновесия в рамках нашего приближения не изменит своей длины. Действительно, длина
x2 |
|
∂u |
2 |
x2 |
|
l = ∫ |
dx ≈ |
∫ dx = x2 − x1. |
|||
1+ |
|
||||
x1 |
|
∂x |
|
x1 |
|
|
|
|
Следовательно, по закону Гука, натяжение T (x, t) будет оставаться постоянным, не зависящим от x, t : T (x, t) =T0.
Пусть ρ(x) – линейная плотность струны в точке х, так что
ρ(x)∆x – масса элемента ∆x струны M1M2.
Составим уравнение движения струны. На ее элемент M1M2
действуют силы натяжения T2 (x + ∆x,t) =T0 и T1(x, t) =T0 , сумма которых, согласно второму закону Ньютона, равна произведению массы этого элемента на его ускорение. Проектируя это векторное равенство на ось u, получим
T |
sin α |
|
|
−T |
sin α |
|
|
=ρ(x)∆x ∂2u , |
(1.1) |
|
|
|
|
||||||
0 |
|
x+∆x |
0 |
|
x |
∂t2 |
|
||
|
|
|
|
|
|
|
|||
4
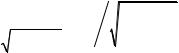
где tg α = |
∂u |
; sin α = |
|
tg α |
|
|
∂x |
|
+ tg |
2 |
α |
||
|
1 |
|||||
|
|
|
||||
Поделим уравнение (1.1) на ∆x :
ρ(x) ∂2u T0
∂t2
1+ ∂u 2∂x
∂u |
|
− |
∂u |
|
|
|
|
|
|||||
∂x |
|
x+∆x |
∂x |
|
x |
|
|
|
|
|
. |
||
|
|
∆x |
|
|||
|
|
|
|
|
|
|
Перейдем в выражении (1.2) к пределу при ∆x →
ρ(x) ∂2u =T0 ∂2u .
∂t2 ∂x2
≈ ∂∂ux .
0 :
(1.2)
(1.3)
Делением уравнения (1.3) на T0 |
получим уравнение свобод- |
||||||||||||||
ных, не зависящих от внешних сил колебаний струны: |
|
||||||||||||||
|
|
1 |
|
|
∂2u |
= |
∂ |
2u |
. |
(1.4) |
|||||
|
|
|
T0 |
|
|
∂t2 |
∂x2 |
||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
||
Поясним смысл отношения T0 / ρ, |
исходя из единиц измерения |
||||||||||||||
рассматриваемых величин: |
|
|
|
|
|
|
|
|
|
|
|
||||
u измеряется в метрах; |
|
|
|
|
|
|
|
|
|
|
|
||||
ut′– в метрах в секунду; |
|
|
|
|
|
|
|
|
|
|
|
||||
utt′′ |
– в метрах в секунду в квадрате; |
|
|
|
|
|
|||||||||
′ |
– безразмерная; |
|
|
|
|
|
|
|
|
|
|
|
|||
ux |
|
|
|
|
|
|
|
|
|
|
|
||||
u′xx |
измеряется в метрах в минус первой степени. |
|
|||||||||||||
Таким образом, величина |
|
T0 / ρ |
имеет размерность квадрата |
||||||||||||
скорости. |
|
|
|
|
|
|
|
|
|
|
|
||||
Обозначим T / ρ = v 2. Тогда (1.4) перепишется в виде |
|
||||||||||||||
|
0 |
|
|
|
2u |
|
|
2u |
|
|
|
|
|||
|
|
1 ∂ |
= |
∂ |
, |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
v 2 ∂t2 |
∂x2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||
или |
|
|
∂2u = v 2 ∂2u |
|
|
|
|||||||||
|
|
|
. |
|
(1.5) |
||||||||||
|
|
|
∂t2 |
|
|
∂x2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
Получим уравнение свободных колебаний струны, или одно-
мерное волновое уравнение.
Покажем, что если ϕ(x) – дважды дифференцируемая функция, то уравнению (1.5) удовлетворяет функция u(x, t) = ϕ(x −vt),
или u(x, t) = u(w) = ϕ(w), |
w = x − vt. |
|
|
|
|||||||||
Действительно, |
|
|
|
|
|
|
|
|
|||||
u′ |
= ϕ′ |
w′ |
= −vϕ′ |
′′ |
= v |
2 |
′′ |
1 |
|
||||
t |
w t |
|
|
w |
utt |
|
ϕww, |
v 2ϕ′′ww = ϕ′′ww, |
|||||
′ |
′ |
′ |
|
|
|
2 |
|||||||
u |
′ |
, |
′′ |
|
|
′′ |
|
|
|||||
|
= ϕ |
|
w |
= ϕ |
w |
|
|
v |
|||||
x |
|
w x |
|
|
uxx = ϕww, |
||||||||
что и требовалось доказать.
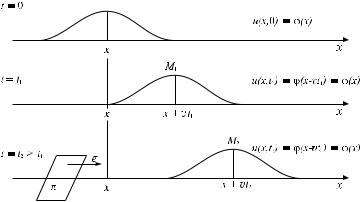
Рис. 2
Частное решение уравнения колебаний струны имеет вид u(x, t) = ϕ(x −vt).
Дадим геометрическую интерпретацию решения. Пусть в начальный момент времени t = 0 был известен профиль струны. Посмотрим, что будет со струной в следующие моменты времени (рис. 2). Точка М на струне движется со скоростью v вправо, при этом ее отклонение остается во все моменты времени постоянным. Это движение называется также плоской волной, которая также движется со скоростью v. Сам процесс колебаний струны описывается волновым уравнением (1.5).
6

1.2. Волновое уравнение для электромагнитных волн
Электромагнитное поле характеризуется напряженностью E(M , t) электрического и H (M , t) магнитного полей, где M (x, y, z) – точка пространства; t – время. Эти величины удовле-
творяют следующим уравнениям Максвелла для непроводящей среды (σ = 0) при отсутствии объемных электрических зарядов:
div |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0, |
rot |
|
= −µµ0 ∂H |
, |
||||||||
E |
E |
||||||||||||
|
|
|
|
|
|
|
∂t |
(1.6) |
|||||
|
|
|
|
|
|
∂ |
|
|
|
|
|||
div H |
= 0, |
|
|
|
|
|
E |
|
, |
|
|||
rot H |
= εε0 |
|
|||||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
∂t |
|
||||||
где ε, µ – диэлектрическая и магнитная проницаемости; ε0 , µ0 –
электрическая и магнитная постоянные в единицах СИ.
Введем векторно-дифференциальный оператор Гамильтона, обозначаемый знаком «набла» :
|
|
|
∂ |
|
∂ |
|
∂ |
|
|
|
|
|
|||||
= |
|
, |
|
, |
|
. |
||
∂x |
∂y |
|
||||||
|
|
|
|
|
∂z |
|||
Тогда система уравнений Максвелла перепишется в следующем виде:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂H |
|
|||
E = 0, |
|
|
|
|
|
|
|
, |
||||||||||
|
|
×E = −µµ0 |
∂t |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.7) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
H = 0, |
×H = εε0 |
∂t |
. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
К последним двум уравнениям применим операцию векторного
умножения на оператор слева и получим систему
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂H |
|
, |
|||||
|
|
|
|
|
|
|
|
|
||||||||||
×( × E ) = −µµ0 × |
∂t |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
∂E |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||
×( × H ) = εε0 × . |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
∂t |
|
|
||||||||
Воспользуемся формулой |
|
векторного |
|
анализа |
||||||||||||||
(1.8)
a ×(b ×c ) =
= b (a c ) −c (a b ). Тогда левые части уравнений будут состоять
7

из двух слагаемых, а операцию дифференцирования и взятия век- торного-дифференциального оператора в правой части можно поменять местами:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
( E ) − |
E = − |
E = −µµ0 |
|
( × H ), |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
∂t |
|
|
(1.9) |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
( |
|
|
|
|
|
|
) − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
( |
|
|
|
|
|
|
|
). |
|
|
|||||||||
|
|
|
|
|
|
2H |
= − |
|
2H |
= εε0 |
|
× |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
H |
|
|
|
E |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
∂t |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Дифференциальный оператор |
|
|
|
|
= |
|
2 = |
|
∂2 |
+ |
∂2 |
+ |
∂2 |
на- |
|||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
∂x2 |
∂y2 |
∂z2 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
зывают оператором Лапласа и обозначают как 2 ≡ ∆.
Так как первые слагаемые в (1.9) равны нулю, выражение (1.9) сократится до вида
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
−∆E = −µµ0 |
|
|
|
|
|
|
εε0 |
|
|
|
|
|
, |
||||||||||||||
∂t |
∂t |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(1.10) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
∂H |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
−∆H = εε0 |
|
|
|
|
−µµ0 |
|
|
|
|
. |
|||||||||||||||||
∂t |
∂t |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Окончательно имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
∂ |
E , |
|
|
|
|
|
|
|||||||||||
∆ |
E |
|
= εε0µµ0 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
∂t |
2 |
|
|
|
|
|
|
|
|
(1.11) |
||||||||||||
|
|
|
|
|
∂2H |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
∆H = εε0µµ0 |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||||||
|
|
∂t |
2 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Два векторных уравнения (1.11) эквивалентны шести скаляр-
ным уравнениям относительно компонент векторов E и H. Все шесть уравнений имеют одинаковый вид. Обозначим через u(M , t) какую-нибудь компоненту какого-либо вектора. Тогда эта
скалярная величина будет удовлетворять уравнению
∆u(M ,t) = εε0µµ0 |
∂2u |
. |
(1.12) |
|
∂t2 |
||||
|
|
|
8
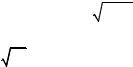
|
Заметим, что |
1 |
|
= c 3 108 м/ c |
– |
скорость света. Пусть |
||||
|
|
|
||||||||
|
|
|
|
ε0µ0 |
|
|
|
|
||
v = |
|
c |
. Тогда уравнение (1.12) для u(M , |
t) примет вид |
||||||
|
εµ |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆u(M , t) = |
1 ∂2u |
. |
(1.13) |
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
v 2 ∂t2 |
|||||
|
|
|
|
|
|
|
|
|
||
Уравнение (1.13) – волновое уравнение для электромагнитных волн. Решение уравнения (1.13) будем называть волной.
Волновое уравнение (1.13) является математической моделью различных физических процессов. Рассмотрим в качестве примера некоторые из них.
1.Пусть точка M (x) принадлежит одномерному пространству
–прямой Ox, тогда однородное волновое уравнение имеет вид
utt′′ (x, t) = v 2u′′xx |
(1.14) |
и описывает свободные поперечные колебания струны или свободные продольные колебания стержня. Если же на струну или стержень кроме упругих сил действуют внешние возмущающие силы F(x, t), то уравнение колебаний называется неоднородным:
|
|
|
|
|
utt′′ (x, t) = v 2u′′xx + f (x, t), |
(1.15) |
где |
f (x, t) = |
v |
2F(x, t) |
; |
ρ(x) – плотность струны или стержня. |
|
|
ρ(x) |
|||||
|
|
|
|
|
|
|
Получающееся при этом решение называют вынужденными колебаниями. Если струна или стержень ограничены, то задаются граничные условия на обоих концах, а также начальные условия. Начальные условия задаются, например, в виде начального профиля u(x, 0) и начального импульса ut′(x, 0) в момент t = 0. В
этом случае уравнения (1.14) и (1.15) называют уравнениями ги-
перболического типа.
2.Пусть точка M (x, y) принадлежит двумерному пространству
–плоскости xOy. Тогда однородное волновое уравнение
utt′′ (x, y, t) = v 2 (uxx′′ +u′′yy ) |
(1.16) |
|
9 |
можно рассматривать как уравнение свободных колебаний плоской мембраны, а неоднородное уравнение
utt′′ (x, y, t) = v 2 (u′′xx +u′′yy ) + f (x, y, t) |
(1.17) |
рассматривать как уравнение вынужденных колебаний мембраны. При этом начальные условия задают начальное положение мембраны и распределение начальных скоростей на ней, а граничные условия задаются способами закрепления границ мембраны.
Если же струна, стержень или мембрана неограниченны, то в качестве граничных условий задают поведение решения на бесконечности, которое, как правило, на бесконечности должно стремиться к нулю.
3. Пусть точка M (x, y, z) принадлежит трехмерному про-
странству. Тогда волновое уравнение можно рассматривать как уравнение малых колебаний газа, заключенного в сферическую оболочку с соответствующими начальными условиями в момент времени t = 0 и граничными условиями на сфере, или как уравнение электромагнитных колебаний, свободных или вынужденных, по аналогии с изложенным в пп. 1 и 2.
Основная проблема, возникающая при исследовании всех этих уравнений и многих других, – это построение решения. Опустим вопрос построения корректного решения [1] и просто перечислим некоторые методы нахождения решения дифференциальных уравнений в частных производных: метод разделения переменных Фурье, метод нахождения обобщенного решения с помощью интегральных преобразований Фурье и Лапласа, метод функции Грина или источника, приближенные методы, например сеточные, и т. д.
Вданном пособии рассматривается, в основном, метод решения с помощью функции Грина.
Метод разделения переменных можно применять, когда функции, входящие в уравнение, в граничные и начальные условия, могут быть разложены в ряд Фурье по собственным функциям, т. е. функции должны, например, удовлетворять условиям Дирихле и быть периодическими, при этом допускается конечное число точек разрыва у функций с конечными скачками.
Вслучае бесконечного скачка в точке x0 , как, например, в
случае с дельта-функцией, приходится пользоваться интегральным
10
