- •Аннотация
- •Пособие может быть использовано также для других специальностей и направлений, при подготовке магистерских и кандидатских диссертаций введение
- •Техническое задание
- •Основная часть
- •1. Формирование статистического распределения
- •2. Расчет координаты центра опытного распределения
- •3. Расчет оценок стандартных отклонений
- •4. Идентификация закона распределения методом моментов
- •5. Устранение грубых ошибок многократных измерений
- •6. Исключение прогрессирующей систематической погрешности
- •7. Критерии нормальности опытного распределения
- •8. Определение случайной погрешности результата измерения
- •9. Проверка однородности дисперсий
- •10. Определение значимости корреляционной связи
- •11. Аппроксимация элементарными функциями
- •12. Регрессия полиномами Чебышева
- •13. Устранение грубых ошибок совместного измерения
- •14. Анализ коэффициентов уравнения регрессии
- •15. Проверка адекватности модели
- •16. Прогнозирование по уравнению регрессии
- •Приложение 1
- •Приложение 2
- •Приложение 3
- •Приложение 4
- •Приложение 5
- •Приложение 6
- •Приложение 7
- •Список литературы
10. Определение значимости корреляционной связи
Если измеряемые величины зависимы друг от друга, то они называются коррелированными, в противном случае – некоррелированными. Степень такой зависимости определяется коэффициентом корреляции.
Пусть имеются две
выборки
![]() и
и
![]() объемом n,
тогда оценка коэффициента корреляции
случайных величин
объемом n,
тогда оценка коэффициента корреляции
случайных величин
![]() и
и
![]() определяется выражением
определяется выражением
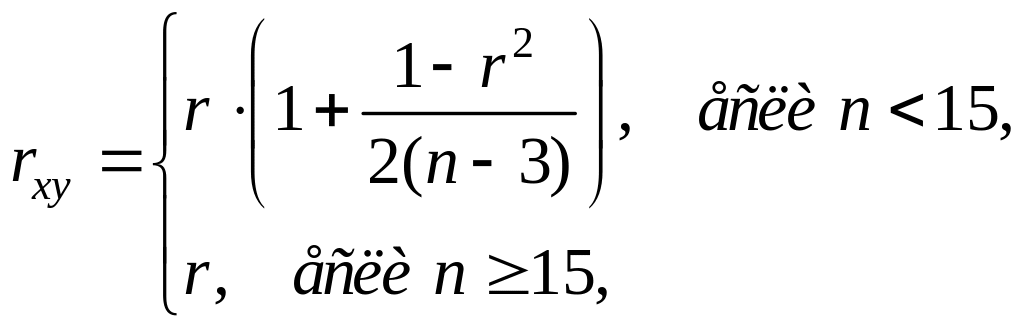
где
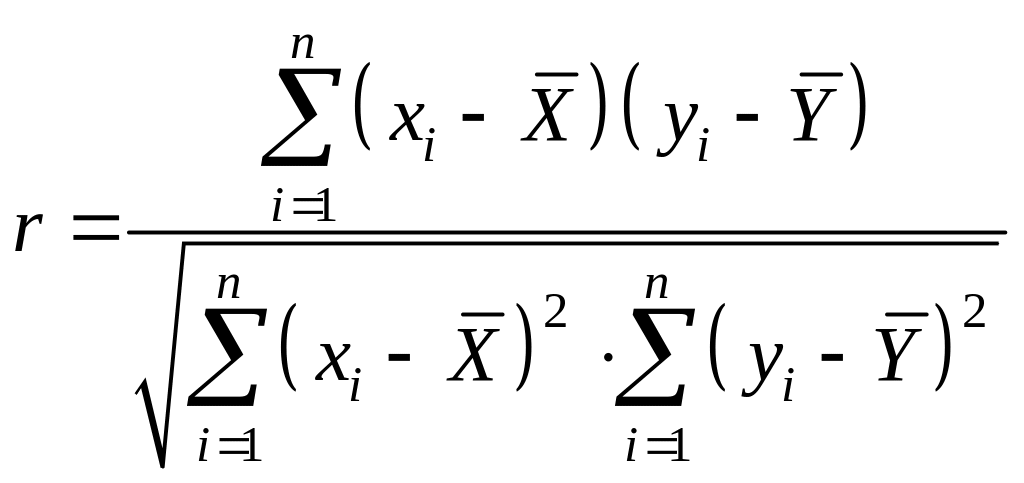 ,
,
,
![]() –
средние арифметические значения.
–
средние арифметические значения.
Значимость корреляционной связи между величинами и определяется проверкой статистической гипотезы.
Наблюдаемым значением критерия при этом является модуль оценки коэффициента корреляции, т.е.
![]() .
.
Критическое
значение критерия
![]() определяется в зависимости от объема
результатов наблюдений n
и значения доверительной вероятности
р
определяется в зависимости от объема
результатов наблюдений n
и значения доверительной вероятности
р
– при
![]()
![]() ,
,
где
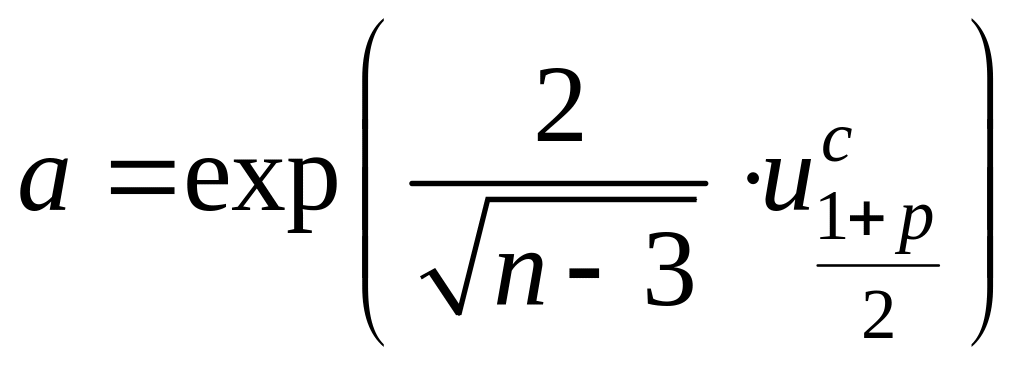 ,
,
![]() –
квантиль стандартного
нормального распределения (Приложение
1, формула ),
–
квантиль стандартного
нормального распределения (Приложение
1, формула ),
– при
![]()
![]() ,
,
где
![]() – квантиль распределения Стьюдента с
числом степеней свободы
– квантиль распределения Стьюдента с
числом степеней свободы
![]() (Приложение 3, формула ),
(Приложение 3, формула ),
– при
![]()
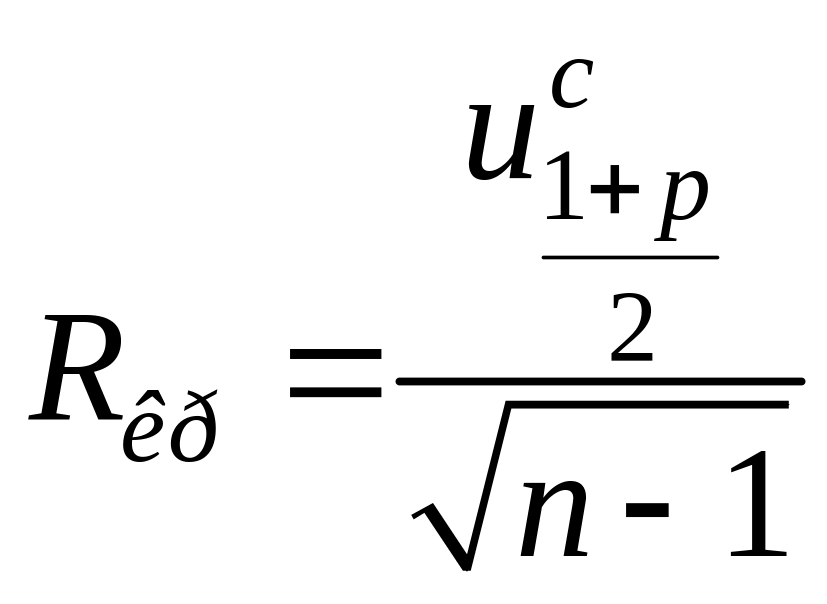
где – квантиль стандартного нормального распределения (Приложение 1, формула ),
Корреляционная связь признается значимой с вероятностью р, если
![]() .
.
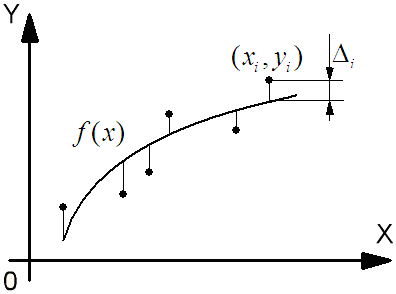
11. Аппроксимация элементарными функциями
Пусть заданы
значения аргумента
![]() некоторой функции, называемые узлами,
и соответствующие им значения этой
функции
некоторой функции, называемые узлами,
и соответствующие им значения этой
функции
![]() .
Необходимо определить аналитический
вид функции
.
Необходимо определить аналитический
вид функции
![]() ,
близко проходящей через точки
,
близко проходящей через точки
![]() .
Решение этой задачи называется
аппроксимацией, а функция
.
Решение этой задачи называется
аппроксимацией, а функция
![]() называется аппроксимирующей.
называется аппроксимирующей.
|
Критерием близости аппроксимирующей функции к экспериментальным точкам в методе наименьших квадратов является минимальная сумма квадратов уклонений, т.е.
|
Аппроксимация
может быть линейной, когда используется
функция
![]() и нелиней-ной.
и нелиней-ной.
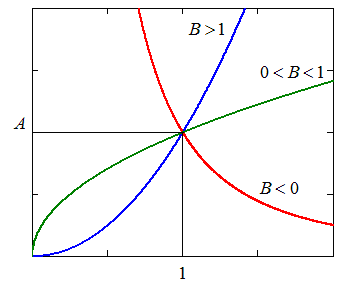
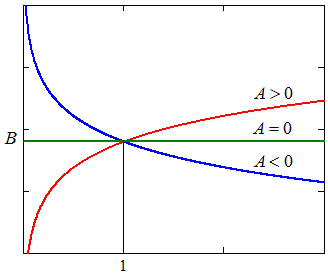
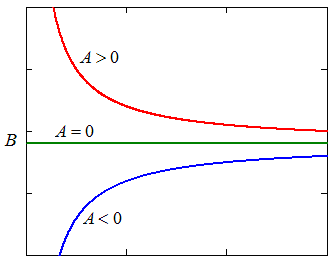
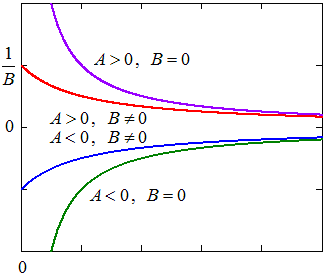
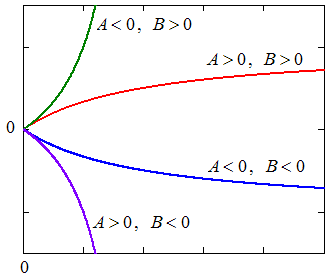
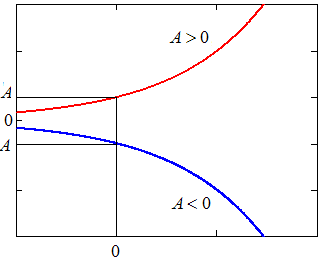
В качестве аппроксимирующих чаще всего используются следующие нелинейные функции
.Степенная |
|
|
Логарифмическая |
|
|
Гиперболическая |
|
|
Дробно-линейная 1 |
|
|
Дробно-линейная 2 |
|
|
Показательная |
|
|
Выбор аппроксимирующей функции может проводится двумя методами:
1. Рассчитываются уклонения для нескольких функций и выбирается функция с минимальным значением критерия .
2. Аппроксимирующая функция методом замены переменных преобразуется к линейному виду (метод выравнивания)
Исходная функция |
Замена переменных |
Выровненная функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция наилучшим образом проходит через экспериментальные точки, если эти точки в новой системе координат лежат на одной прямой. Для этого нужно, чтобы разделенные разности первого порядка
![]()
были примерно (а в идеальном случае строго) равны, т.е.
![]() .
.
Таким образом, алгоритм выбора аппроксимирующей функции методом выравнивания следующий:
Рассчитываются разделенные разности первого порядка по координатам экспериментальных точек . Если они равны, то в качестве аппроксимирующей выбирается линейная функция. В противном случае переход к шагу 2.
Экспериментальные точки пересчитываются в новую систему координат для нелинейных функций.
Вычисляются значения разделенных разностей первого порядка по формулам .
Выбирается та функция, для которой значения разделенных разностей наиболее близки друг к другу.
Коэффициенты А и В выбранной функции рассчитываются через вспомогательные коэффициенты Р и Q, которые определяются по формулам
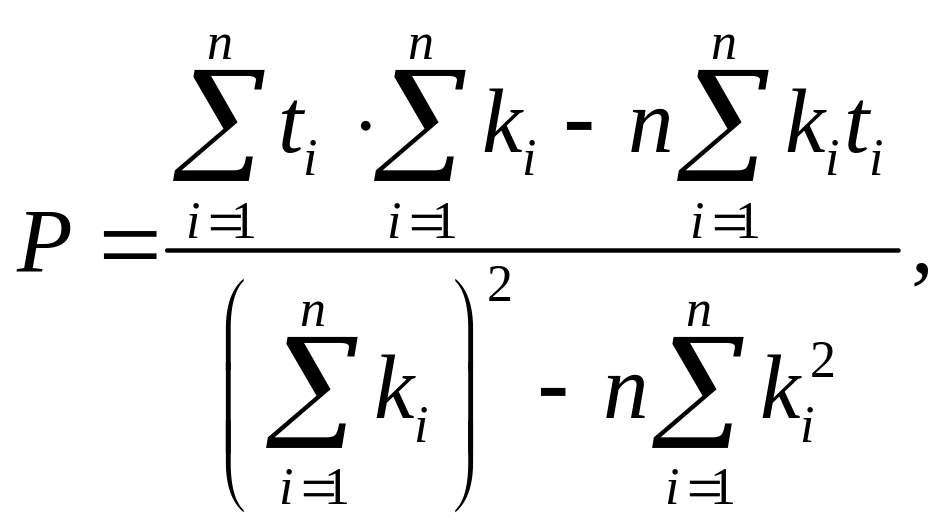
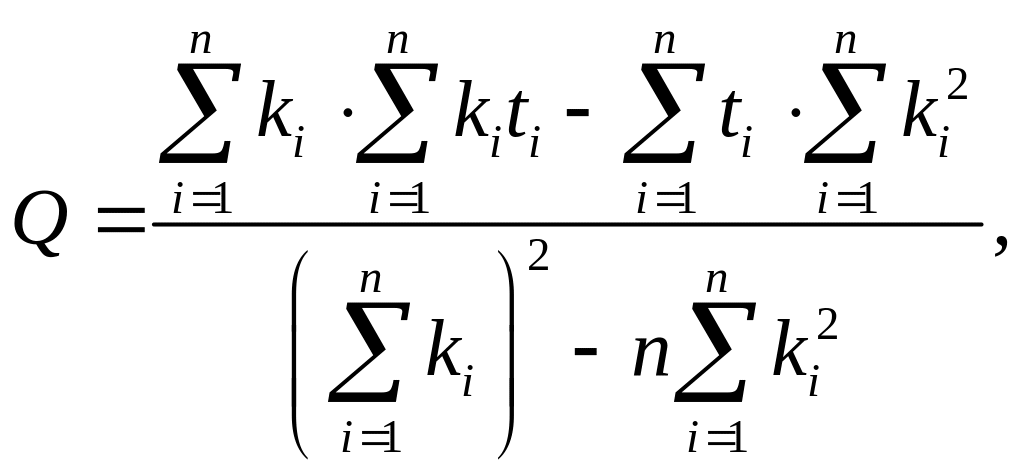
где
Аппроксимирующая функция |
А |
B |
Переменные |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
, |
|
|
|
,
|
|
|
|
|
|
|
|
,
|
Альтернативным методом поиска уравнения регрессии является аппроксимация полиномами Чебышева.