3. Максимальное правдоподобие

Если при выработке правила выбора решений нет ника­ких данных относительно априорных вероятностей состоя­ний и , то вместо рассмотренного критерия можно применить критерий максимума правдоподобия, согласно которому при наблюдении выборки принимает­ся та из гипотез, которой соответствует большее значение функции правдоподобия выборки. Таким образом, прини­мается гипотеза , если , и отвергается эта гипотеза, если . Иначе говоря, принимается решение если для наблюдаемой выборки

(31)

В противном случае принимается решение . Процедура проверки простой гипо­тезы по критерию максимального правдоподобия сводится к вычислению отношения правдоподобия и сравнению его с единицей. Отличие от правила, соответствующего макси­муму апостериорной вероятности, состоит лишь в замене обобщенного отношения правдоподобияотношением правдоподобия.

Следовательно, правило выбора решения по критерию максимального правдоподобия является частным случаем правила по критерию максимума апостериорной вероятно­сти, когда два возможных состояния изучаемого явления и равновероятны, т. е. когда .

4. Критерий Неймана-Пирсона

Другой подход к выработке правила выбора решений при отсутствии априорной информации о потерях и вероятностях состояний указывает критерий Неймана - Пирсона. Согласно этому критерию выбирается такое правило, которое обеспечивает минимально возможную величину вероятности ошибок второго рода при условии, что вероятность ошибки перво­го рода не больше заданной величины .

Теорема Неймана - Пирсона: Среди всех критериев, различающих гипотезы u с заданной ошибкой первого рода , наиболее мощным является критерий отношения правдоподобия.

Согласно теореме Неймана - Пирсона, существует такая конс­танта С, зависящая только от , что критическая область наиболее мощного критерия имеет вид

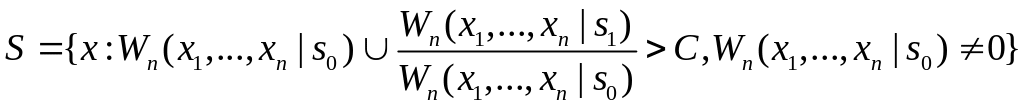
При этом константа С является решением уравнения

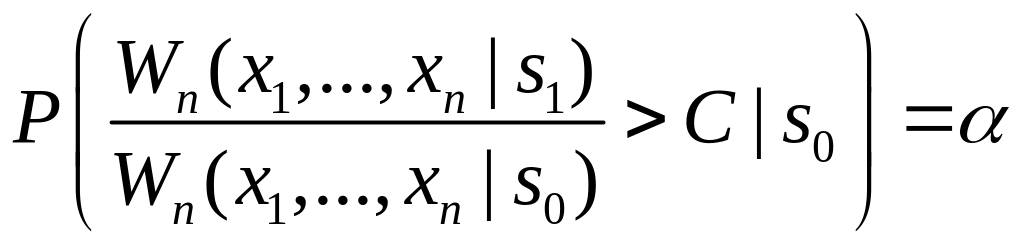(32)

Правило выбора решения по критерию Неймана - Пирсона имеетнаибольшую мощность среди всех других правил, для которых уровень значимости не превосходит . Следовательно, нужно максимизировать величину

,

при условии

₍₃₃₎

Множество не меняет размера критерия , но увеличивает его мощность. Считая, что , рассмотрим случай . Тогда

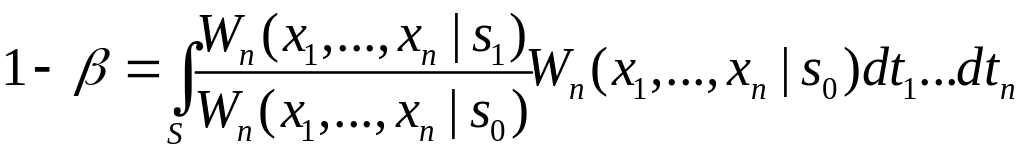
при условии

Следовательно, максимизи­руется среднее значение случайной величины при условии истинности нулевой гипотезы .

Можно заключить, что прави­ло выбора решений, базирующееся на критерии Нейма­на — Пирсона, является частным случаем байесовского решения, в котором величина заменяется величину опреде­ляемую уравнением (32).

Итак, все рассмотренные выше критерии качества при­водят к единообразной процедуре принятия решения: по наблюденной выборке вычисляется отноше­ние правдоподобия и принимается или отвер­гается гипотеза в зависимости от того, находится ли эта величина ниже или выше некоторого фиксированного поро­га, устанавливаемого заранее в соответствии с принятым критерием.