
- •Оглавление
- •Список используемых сокращений
- •Введение
- •Понятие и сущность статистических гипотез
- •1.1.Постановка проблемы
- •1.2. Статистический критерий
- •Классификация статистических критериев:
- •1.3. Функция потерь и критерий качества выбора решения
- •2. Проверка простой гипотезы против простой альтернативы
- •2.1. Вероятности правильных и ошибочных решений
- •Критерии принятия решений
- •Байесовское решение
- •Максимум апостериорной вероятности
- •Максимальное правдоподобие
- •Критерий Неймана-Пирсона
- •Минимаксное правило
- •Критерии значимости
- •3.1. Проверка гипотез для нормального распределения
- •3.1.1. Гипотезы о неизвестном среднем при известной дисперсии
- •3.1.2. Гипотезы о неизвестном среднем при неизвестной дисперсии
- •3.1.3. Гипотеза о неизвестной дисперсии
- •3.2. Сравнение средних нормального распределения
- •3.2.1. Проверка гипотез о равенстве средних для двух выборок
- •3.2.1.1. Гипотеза о равенстве средних при неизвестных равных дисперсиях
- •3.2.1.2. Гипотеза о равенстве средних при известных дисперсиях
- •3.2.1.3. Сравнение средних при неизвестных неравных дисперсиях
- •3.2.1.3.1. Критерий Кохрана-Кокса
- •3.2.1.3.2. Критерий Сатервайта
- •3.2.2. Проверка гипотез о равенстве средних для выборок
- •3.2.2.1. Критерий Полсона
- •3.2.2.2. Критерий Шеффе
- •3.3. Сравнение дисперсий нормального распределения
- •3.3.1. Проверка гипотез о равенстве дисперсий для двух выборок
- •3.3.1.1. Критерий Фишера
- •3.3.1.2. Критерий Романовского
- •3.3.2. Проверка гипотез о равенстве дисперсий для выборок
- •3.3.2.1. Критерии Бартлетта
- •3.3.2.2. Критерии Кохрена
- •3.3.2.3. Критерий Самиуддина
- •3.4. Проверка гипотез для экспоненциального распределения
- •3.4.1. Гипотеза о неизвестном параметре экспоненциального распределения
- •4. Общие критерии согласия
- •4.1.Критерии хи-квадрат Пирсона
- •4.2. Критерии хи-квадрат Фишера
- •4.3. Критерий согласия Колмогорова- Смирнова
- •4.4. Критерий Смирнова-Крамера-фон Мизеса
- •4.5. Критерий Андерсона-Дарлинга
- •4.6. Критерий согласим Дарбина
- •5. Частные критерии согласия
- •5.1. Критерии проверки нормальности распределения
- •5.1.1. Сравнительный анализ критериев нормальности
- •5.1.2. Критерий Шапиро-Уилка
- •5.1.3 Критерий
- •5.1.4 Критерий
- •5.1.5 Критерий
- •5.1.6. Критерий нормальности д'Агостино
- •5.1.7. Энтропийный критерий нормальности (критерий Васичека)
- •5.1.8. Критерий Дэвида-Хартли-Пирсона
- •5.2. Критерии проверки экспоненциальности распределения
- •5.2.1. Критерий Фроцини
- •5.2.2. Критерий Бартлетта-Морана
- •5.3. Критерии проверки равномерности распределения
- •5.3.1. Критерий Ченга – Спиринга
- •5.3.2. Критерий Саркади – Косика
- •5.4. Критерии симметрии
- •5.4.1. Критерий симметрии Смирнова
- •5.4.2. Одновыборочный критерий Вилкоксона
- •6. Критерии однородности
- •6.1. Критерий -квадрат
- •6.2. Критерий Колмогорова
- •6.3. Критерий Уилкоксона — Манна — Уитни
- •7. Подбор кривых распределения вероятностей по экспериментальным данным
- •7.1. Кривые Пирсона типа I
- •7.2. Кривые Пирсона типа II
- •7.3. Кривые Пирсона типа III
- •7.4. Кривые Пирсона типа IV
- •7.5. Кривые Пирсона типа V
- •7.6. Кривые Пирсона типа VI
- •7.7. Кривые Пирсона типа VII
- •Список используемой литературы
5.1.2. Критерий Шапиро-Уилка
Критерий
Шапиро-Уилка
является наиболее эффективным критерием
проверки гипотезы о принадлежности
выборки к нормальному закону распределения.
Следует отметить, что критерий работает
одинаково эффективно и при малых и при
больших объемах выборки. Критерий можно
применять при
объеме
выборки
![]() .
.
Критерий Шапиро-Уилка [45] основан на отношении оптимальной линейной несмещенной оценки дисперсии к ее обычной оценке методом максимального правдоподобия. Статистика критерия имеет вид
 (124)
(124)
где
 (125)
(125)
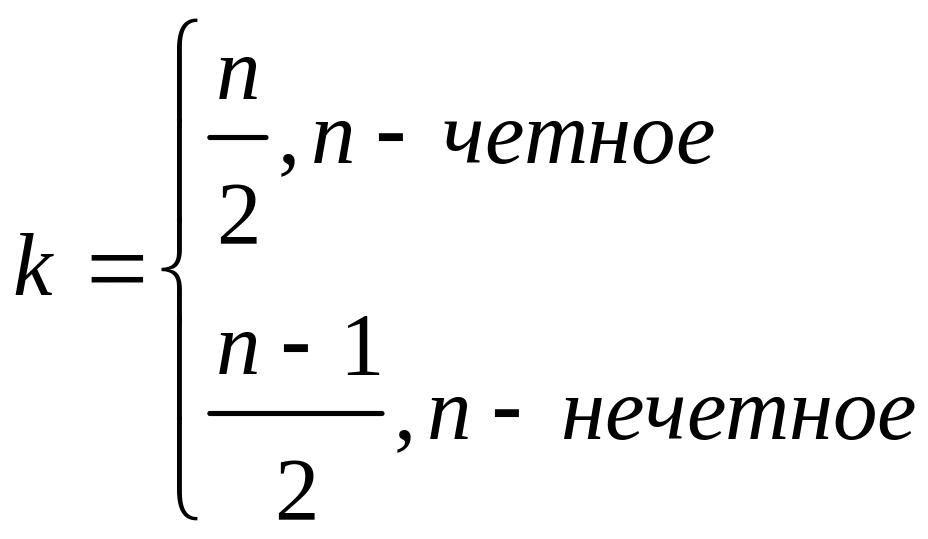 (126)
(126)
- среднее арифметическое выборки, определяемое по формуле (39).
Числитель является квадратом оценки среднеквадратического отклонения Ллойда [46].
Коэффициенты
![]() приведены
втаблице 12, заимствованной из [47,45].
Критические значения статистики
приведены
втаблице 12, заимствованной из [47,45].
Критические значения статистики
![]() приведены втаблице 11, заимствованной
из [47, 45].
приведены втаблице 11, заимствованной
из [47, 45].
Если
![]() ,
то нулевая гипотеза нормальности
распределения отклоняется на уровне
значимости
.
Приближенную вероятность получения
эмпирического значения
при
можно вычислить по формуле [48]:
,
то нулевая гипотеза нормальности
распределения отклоняется на уровне
значимости
.
Приближенную вероятность получения
эмпирического значения
при
можно вычислить по формуле [48]:
 (127)
(127)
где
,
![]() и
и
![]() - коэффициенты, приведенные втаблице
10.
- коэффициенты, приведенные втаблице
10.
Для больших таблицы коэффициентов становятся неудобными, поэтому была предложена модификация критерия Шапиро-Уилка - критерий Шапиро - Франчиа [49].
При этом коэффициенты определяются соотношением:
 (128)
(128)
где
![]() –
квантиль стандартного нормального
распределения при
–
квантиль стандартного нормального
распределения при![]() .
.
Используя аппроксимацию для квантили стандартного нормального распределения, можно записать:
![]() (129)
(129)
Тогда для заданного :
 (130)
(130)
В [50] приведена полезная аппроксимация, позволяющая применить критерий Шапиро - Уилка без помощи таблиц.
Для
наиболее распространенного в технических
измерениях значения доверительной
вероятности
![]() (уровне
значимости
(уровне
значимости
![]() )
можно применять модификацию
-
критерия, позволяющую обойтись без
таблиц критических значений.
)
можно применять модификацию
-
критерия, позволяющую обойтись без
таблиц критических значений.
Наблюдаемое значение критерия при этом можно определить по формуле
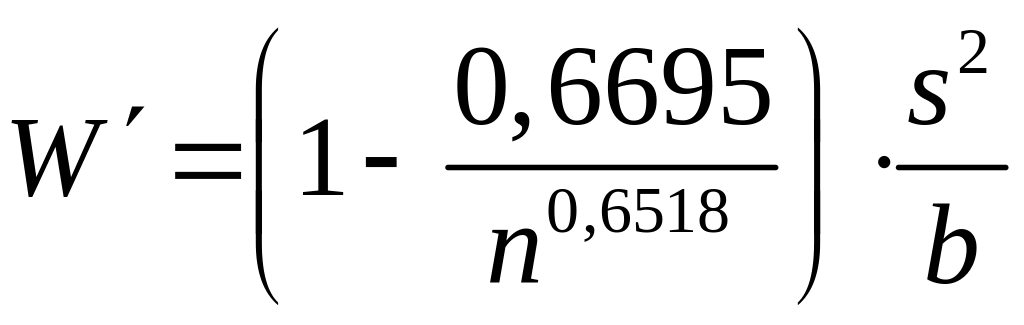 (131)
(131)
где – коэффициент, вычисляемый по формуле(125)
 (132)
(132)
– вычисляется по формуле(126)
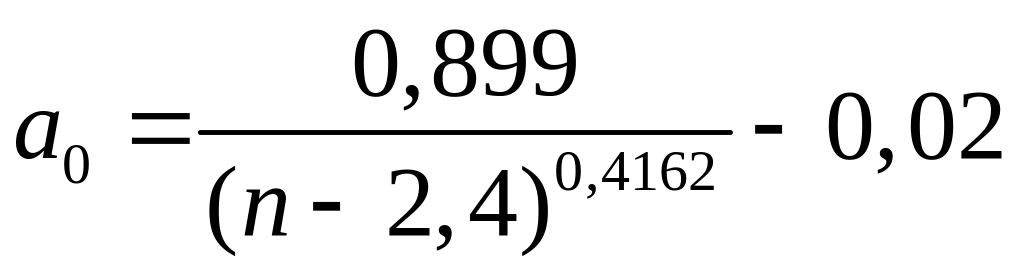 (133)
(133)
 (134)
(134)
 (135)
(135)
где – объем выборки.
Если
![]() ,
то нулевая гипотеза нормальности
распределения случайных величин
отклоняется. Модификация критерия
Шапиро - Уилка для случая группированных
данных (что существенно при наличии
совпадающих наблюдений) рассмотрена в
[51].
,
то нулевая гипотеза нормальности
распределения случайных величин
отклоняется. Модификация критерия
Шапиро - Уилка для случая группированных
данных (что существенно при наличии
совпадающих наблюдений) рассмотрена в
[51].
Таблица 10. Значения коэффициентов , и
|
|
|
|
|
|
|
|
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
-0,6250 -1,1070 -1,5300 -2,0100 -2,3560 -2,6960 -2,9680 -3,2620 -3,4850 -3,7310 -3,9360 -4,1550 -4,3730 -4,5670 -4,7130 -4,8850 -5,0180 -5,1840 -5,2910 -5,4130 -5,5080 -5,6050 -5,7040 -5,8030 |
0,3860 0,7140 0,9350 1,1380 1,2450 1,3330 1,4000 1,4710 1,5150 1,5710 1,6130 1,6550 1,6950 1,7240 1,7390 1,7700 1,7860 1,7980 1,8180 1,8350 1,8480 1,8620 1,8760 1,8900 |
0,7500 0,6297 0,5521 0,4963 0,4533 0,4186 0,3900 0,3660 0,3451 0,3270 0,3111 0,2969 0,2842 0,2727 0,2622 0,2528 0,2440 0,2375 0,2264 0,2207 0,2157 0,2106 0,2063 0,2020 |
27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
-5,9050 -5,9880 -6,0740 -6,1600 -6,2480 -6,3240 -6,4020 -6,4800 -6,5590 -6,6400 -6,7210 -6,8030 -6,8870 -6,9610 -7,0350 -7,1110 -7,1880 -7,2120 -7,2660 -7,3450 -7,4140 -7,5550 -7,6150 -7,6770 |
1,9050 1,9150 1,9340 1,9490 1,9650 1,9760 1,9880 2,0000 2,0120 2,0240 2,0370 2,0490 2,0620 2,0750 2,0880 2,1010 2,1140 2,1190 2,1280 2,1410 2,1550 2,1830 2,1980 2,2120 |
0,1980 0,1943 0,1907 0,1872 0,1840 0,1811 0,1781 0,1755 0,1727 0,1702 0,1677 0,1656 0,1633 0,1612 0,1591 0,1572 0,1552 0,1548 0,1534 0,1526 0,1499 0,1466 0,1451 0,1436 |
Таблица 11. Таблица критических значений
n |
p=0.99 |
p=0.98 |
p=0.95 |
p=0.90 |
n |
p=0.99 |
p=0.98 |
p=0.95 |
p=0.90 |
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
0.737 0.687 0.686 0.713 0.730 0.749 0.764 0.781 0.792 0.805 0.814 0.825 0.835 0.844 0.851 0.858 0.863 0.868 0.873 0.878 0.881 0.884 0.888 0.891 |
0.756 0.707 0.715 0.743 0.760 0.778 0.791 0.806 0.817 0.828 0.837 0.846 0.855 0.863 0.869 0.874 0.879 0.884 0.888 0.892 0.895 0.889 0.901 0.904 |
0.767 0.748 0.762 0.788 0.803 0.818 0.829 0.842 0.850 0.859 0.866 0.974 0.881 0.887 0.892 0.897 0.901 0.905 0.908 0.911 0.914 0.916 0.918 0.920 |
0.789 0.792 0.806 0.826 0.838 0.851 0.859 0.869 0.876 0.883 0.889 0.895 0.901 0.906 0.910 0.914 0.917 0.920 0.923 0.926 0.928 0.930 0.931 0.933 |
27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
0.894 0.896 0.898 0.900 0.902 0.904 0.906 0.908 0.910 0.912 0.914 0.916 0.917 0.919 0.920 0.922 0.923 0.924 0.926 0.927 0.928 0.929 0.929 0.930 |
0.906 0.908 0.910 0.912 0.914 0.915 0.917 0.919 0.920 0.922 0.924 0.925 0.927 0.928 0.929 0.930 0.932 0.933 0.934 0.935 0.936 0.937 0.937 0.938 |
0.923 0.924 0.926 0.927 0.929 0.930 0.931 0.933 0.934 0.935 0.936 0.938 0.939 0.940 0.941 0.942 0.943 0.944 0.945 0.945 0.946 0.947 0.947 0.947 |
0.935 0.936 0.937 0.939 0.940 0.941 0.942 0.943 0.944 0.945 0.946 0.947 0.948 0.949 0.950 0.951 0.951 0.952 0.953 0.953 0.954 0.954 0.955 0.955 |
Таблица
12. Коэффициенты![]()
|
|
||||||||||||||||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
7071 6872 6646 6431 6233 6052 5888 5739 5601 5475 5359 5251 5150 5056 4968 4886 4808 4734 4634 4590 4542 4493 4450 4407 4366 4328 4291 4254 4220 4188 4156 4127 4096 4068 4040 4015 3989 3964 3940 3917 3894 3872 3850 3830 3808 3789 3770 3751 |
1677 2413 2806 3031 3164 3244 3291 3315 3325 3325 3318 3306 3290 3273 3253 3232 3211 3185 3156 3126 3098 3069 3043 3018 2992 2968 2944 2921 2898 2876 2854 2834 2813 2794 2774 2755 2737 2719 2701 2684 2667 2651 2635 2620 2604 2589 2574 |
0875 1401 1743 1976 2141 2260 2347 2412 2460 2495 2521 2540 2553 2561 2565 2578 2571 2563 2554 2543 2533 2522 2510 2499 2487 2475 2463 2451 2439 2427 2415 2403 2391 2380 2368 2357 2345 2334 2323 2313 2302 2291 2281 2271 2260 |
0561 0947 1224 1429 1586 1707 1802 1878 1939 1988 2027 2059 2085 2119 2131 2139 2124 2148 2151 2152 2151 2150 2148 2145 2141 2137 2132 2127 2121 2116 2110 2104 2098 2091 2085 2078 2072 2065 2058 2052 2045 2038 2032 |
0399 0695 0922 1099 1240 1353 1447 1524 1587 1641 1686 1736 1764 1787 1807 1822 1836 1848 1857 1864 1870 1874 1878 1880 1882 1883 1883 1883 1881 1880 1878 1876 1874 1871 1868 1865 1862 1859 1855 1851 1847 |
0303 0539 0727 0880 1005 1109 1197 1271 1334 1399 143 1480 1512 1539 1563 1584 1601 1616 1630 1641 1651 1660 1667 1673 1678 1683 1686 1689 1691 1693 1694 1695 1695 1695 1695 1695 1693 1692 1691 |
0240 0433 0593 0725 0837 0932 1013 1092 1150 1201 1245 1283 1316 1346 1372 1395 1415 1433 1449 1463 1475 1487 1496 1505 1513 1520 1526 1531 1535 1539 1542 1545 1548 1550 1551 1553 1554 |
0196 0359 0496 0612 0711 0804 0878 0941 0997 1046 1089 1128 1162 1192 1219 1243 1265 1284 1301 1317 1331 1344 1356 1366 1376 1384 1392 1398 1405 1410 1415 1420 1423 1427 1430 |
0173 0303 0422 0530 0618 0696 0764 0823 0876 0923 0965 1002 1036 1066 1093 1118 1140 1160 1179 1196 1211 1225 1237 1249 1259 1269 1278 1286 1293 1300 1306 1312 1317 |
0140 0263 0368 0459 0539 0610 0672 0728 0778 0822 0862 0899 0931 0961 0988 1013 1036 1056 1075 1092 1108 1123 1136 1149 1160 1170 1180 1189 1197 1205 1212 |
0122 0228 0321 0403 0476 0540 0598 0650 0697 0739 0777 0812 0844 0873 0900 0924 0947 0967 0986 1004 1020 1035 1049 1062 1073 1085 1095 1105 1113 |
0107 0200 0284 0358 0424 0483 0537 0585 0629 0669 0706 0739 0770 0798 0824 0848 0870 0891 0909 0927 0943 0959 0972 0986 0998 1010 1020 |
0094 0178 0253 0320 0381 0435 0485 0530 0572 0610 0645 0677 0706 0733 0759 0782 0804 0824 0842 0860 0876 0892 0906 0919 0932 |
0084 0159 0227 0289 0344 0395 0441 0484 0523 0559 0592 0622 0651 0677 0701 0724 0745 0765 0783 0801 0817 0832 0846 |
0076 0144 0206 0262 0314 0361 0404 0444 0481 0515 0546 0575 0602 0628 0651 0673 0694 0713 0731 0748 0764 |
0068 0131 0187 0239 0287 0331 0372 0409 0444 0476 0506 0534 0560 0584 0607 0628 0648 0667 0685 |
0062 0119 0172 0220 0264 0305 0343 0379 0411 0442 0471 0497 0522 0546 0568 0588 0608 |
0057 0110 0158 0203 0244 0283 0318 0352 0383 0412 0439 0465 0489 0511 0532 |
0053 0101 0146 0188 0227 0263 0296 0328 0357 0385 0411 0436 0459 |
0049 0094 0136 0175 0211 0245 0277 0307 0335 0361 0386 |
0045 0087 0126 0163 0197 0229 0259 0288 0314 |
0042 0081 0118 0153 0185 0215 0244 |
0039 0076 0111 0143 0174 |
0037 0071 0104 |
0035 |
Пример 22
Проверить по критерию Шапиро-Уилка принадлежность выборки объемом n=40 к нормальному закону распределения при доверительной вероятности p=0,95. 79 58 54 52 73 67 71 63 85 53 73 67 62 53 41 43 61 52 63 80 72 65 65 77 42 67 64 67 70 68 59 61 75 59 32 69 60 60 60 76 Решение Поскольку доверительная вероятность , то воспользуемся статистикой(131) Вычислим необходимые коэффициенты.
Вычислены
значения
Вычислим
коэффициент
(125)
с помощью найденного ранее значения
СКО
Вычислим
коэффициент
Вычислим
коэффициент
значит
коэффициентов
Вычислим
коэффициенты
Вычислим
коэффициенты
Расположим выборку экспериментальных данных в ранжированный ряд 32 41 42 43 52 52 53 53 54 58 59 59 60 60 60 61 61 62 63 63 64 65 65 67 67 67 67 68 69 70 71 72 73 73 75 76 77 79 80 85 То есть
тогда
коэффициент
и наблюдаемое значение критерия (131)
Поскольку
|





















 .
.
