3.2.2.2. Критерий Шеффе

Среди средних значений, предварительно упорядоченных по величине: , производится сравнений. Например, для производится множественных сравнения

; ; ; .

Если при этом будет превышена критическая разница, то нулевая гипотеза о равенстве средних и отклоняется.

Шеффе предложил использовать в качестве критического значения величину

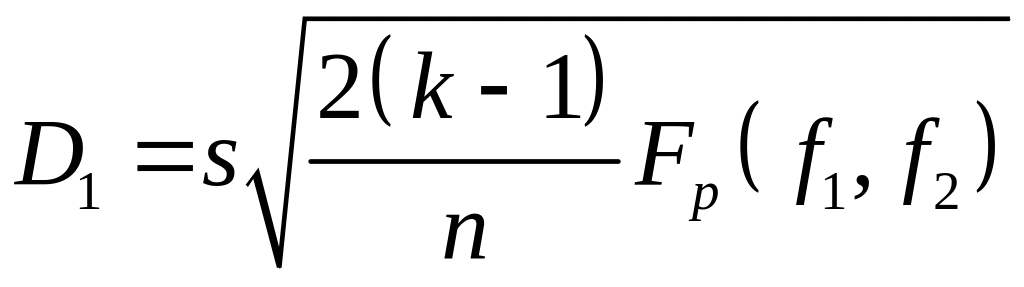(72)

где

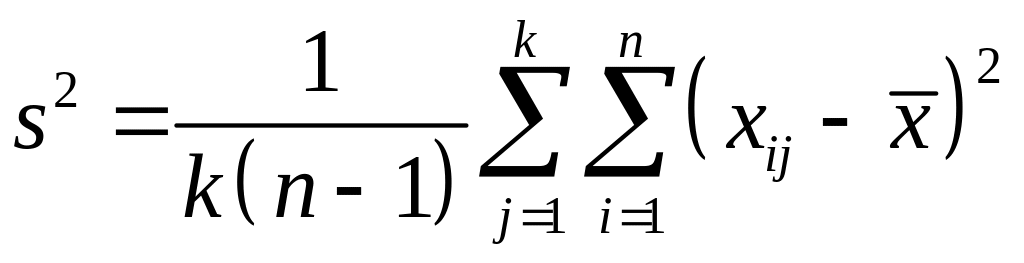(73)

(74)

(75)

- -квантиль распределения Фишера с и степенями свободы. Критерий Шеффе является грубым критерием и особенно пригоден тогда, когда имеется подозрение о неравенстве дисперсий между собой.

Пример 11 В условиях предыдущей задачи требуется проверить гипотезу о статистической неразличимости средних значений долговечности в выборках критерием Шеффе при . Решение Имеем ; ; По формуле (39) вычисляем: ; ; ; ; . Тогда исходя из (52): . Учитывая, что , находим . Следовательно, по формуле (72) находим Максимальная разность: . Так как критерий Шеффе не отклоняет нулевую гипотезу.

3.3. Сравнение дисперсий нормального распределения

Пусть имеются две независимые выборки: и , имеющие нормальное распределение с параметрами и соответственно. Необходимо проверить гипотезу равенства дисперсий и , опираясь на их выборочные оценки и .

3.3.1. Проверка гипотез о равенстве дисперсий для двух выборок

В [6]рассмотрены критерий Фишера, критерий Романовского [16], критерий отношения размахов, критерий «стьюдентизированного» размаха, критерий Аризоно-Охты [17].

Рассмотрим самый популярный критерий проверки данного класса гипотез -критерий Фишера и наиболее простой - критерий Романовского.

3.3.1.1. Критерий Фишера

Пусть основная гипотеза : , альтерна­тивная же гипотеза может быть трех видов: а) ; б) ; в) . Однако случай в) сводится к случаю б) перестановкой и , поэтому не будет рас­сматриваться отдельно.

Поскольку средние неизвестны, наилучшими оценками диспер­сий (52) являются

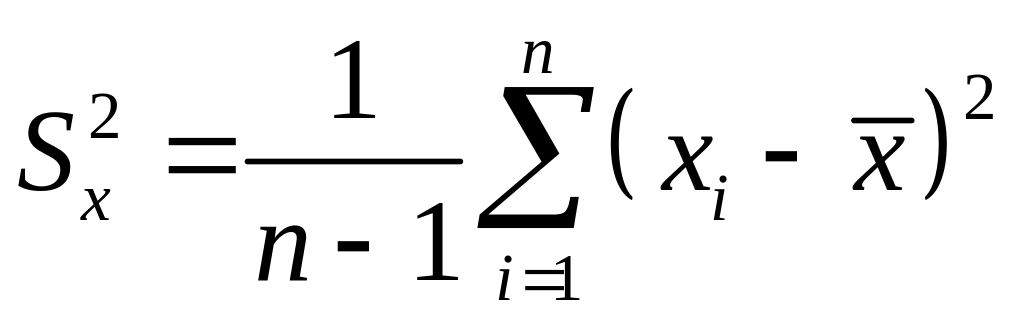и _.

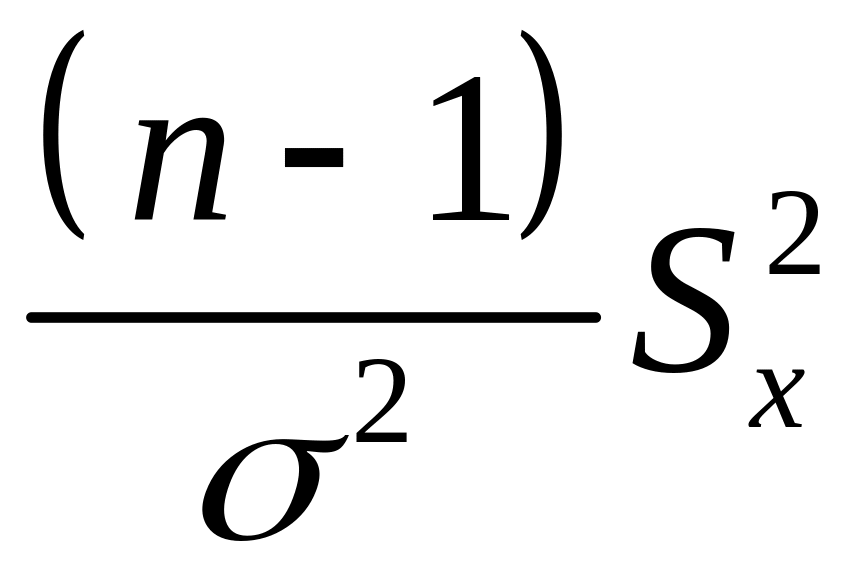Случайные величины и , как следует из теоремы Фи­шера, не зависят от средних, и если справедлива нулевая гипотеза : , то случайные величины и 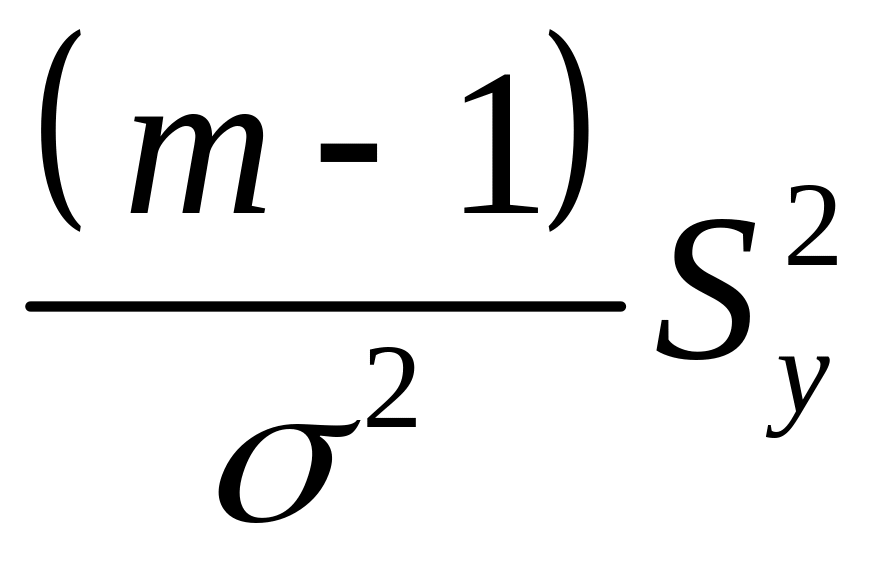имеют распределение с и степенями свободы соответственно. Тогда статистика

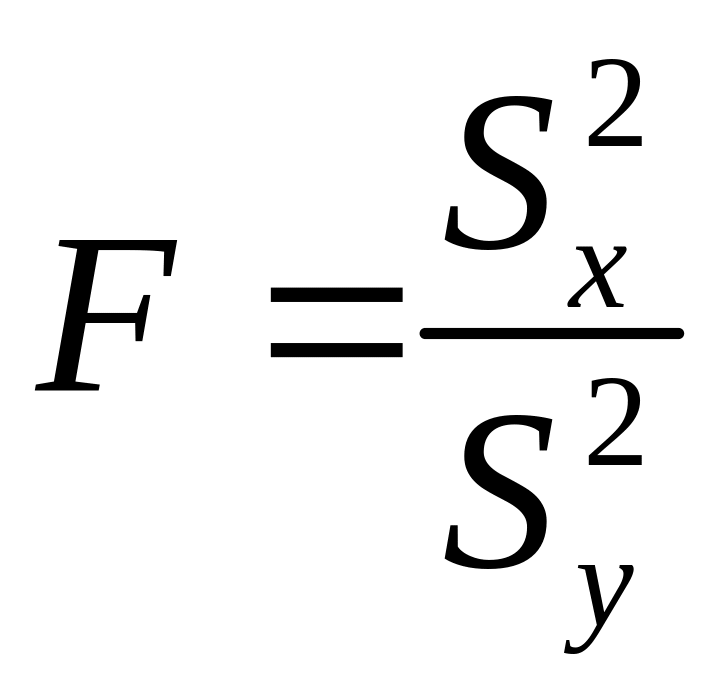(76)

не зависит от параметров нормально­го распределения и имеет распределение Фишера с и степенями свободы. Очевидно, что если дисперсии равны, то отношение их оценок должно быть близким к единице. Поэтому критерий таков: гипотеза отвергается, если или , где . Задача свелась к нахождению констант и . По задан­ному уровню значимости и числу степеней свободы по таблицам распределения Фишера находят квантиль . Для -квантилей Фишера справедливо соотношение

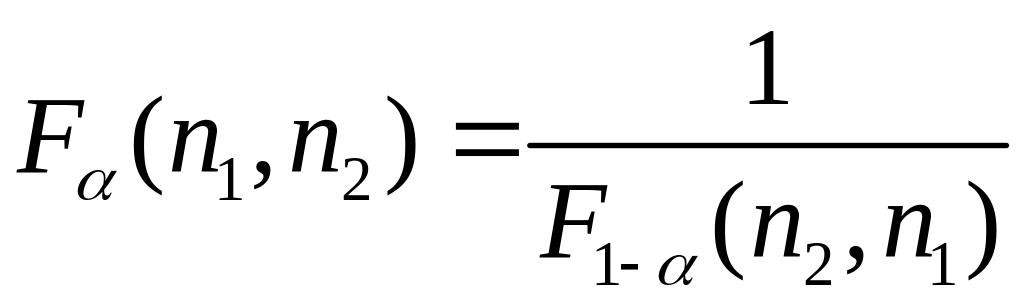₍₇₇₎

Отсюда следует алгоритм проверки гипотезы.

В случае а) делят большую выборочную дисперсию на меньшую:

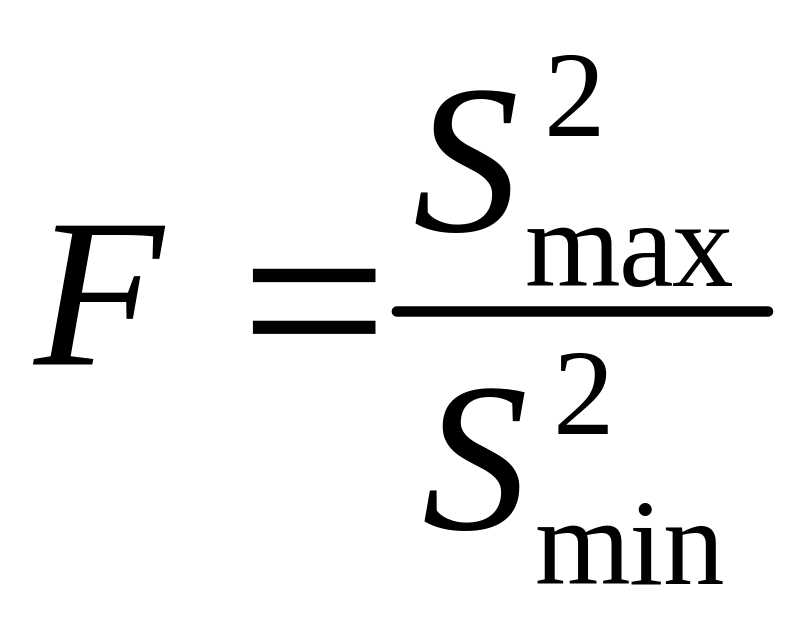₍₇₈₎

Обозначим через объем выборки с меньшей выборочной дисперсией и через - с большей. По таблице для распределе­ния Фишера находим критическую точку с уровнем значимости и числами степеней свободы и . Если , то основная гипотеза принимается, в противном случае отвергается.

В случае б) делят первую выборочную дисперсию на вторую:

По таблице для распределения Фишера находим критическую точку с уровнем значимости и числами степеней свободы и . Если , то основная гипотеза принимается, в противном случае отвергается.

Замечание:Если известны средние распределения и , то

и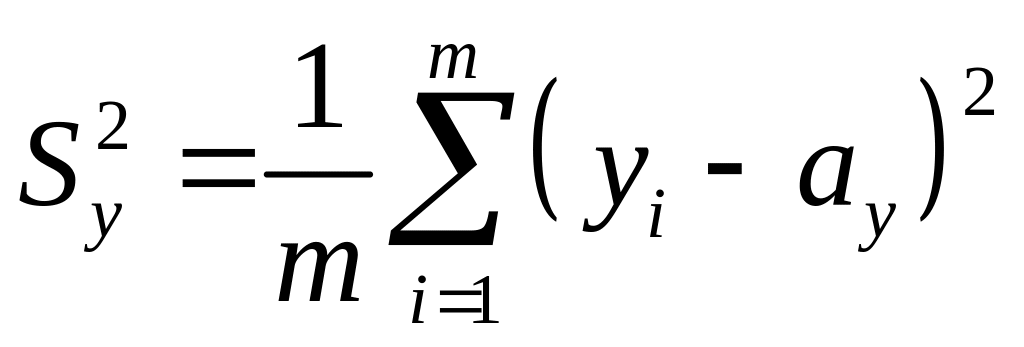

и статистика имеет распределение Фишера с и степенями свободы.

Замечание: Критерий Фишера очень чувствителен к отклонениям от нормальности распределений и .Для повышения устойчивости используется корректировка степеней свободы. Вместо и используются

₍₇₉₎

₍₈₀₎

_где

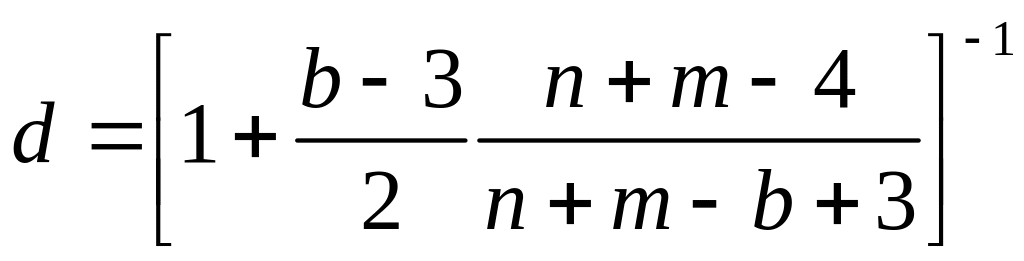₍₈₁₎

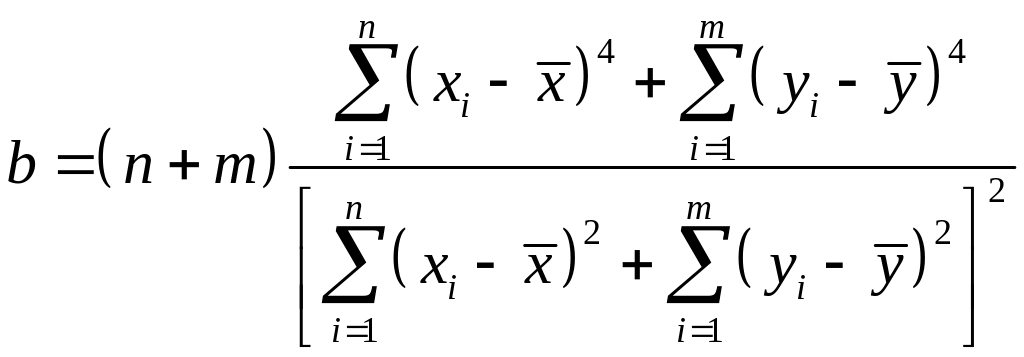₍₈₂₎

В случае если количество серий результатов наблюдений больше двух, то из всех оценок дисперсий выбирают две - с максимальным и минимальным значениями. Если окажется, что различие между ними незначимо, то тем более незначимо и различие между остальными дисперсиями. Недостатком критерии Фишера в этом случае является то, что информация об остальных сериях, кроме имеющих наибольшую и наименьшую дисперсии, не используется.

Пример 12 Имеются две выборки нормально распределенных случайных величин 2,1; 3,1; 4,8; 6,1; 7,4; 8,5; 10,1; 12,1; 14,0; 15,6; 4,6; 6,1; 8,2; 9,8; 9,9; 10,4; 13,1; 14,5; 16,1; 19,1. Необходимо проверить гипотезу равенства дисперсий против альтернативы при доверительной вероятности . Имеем ; ; Далее . Из таблиц находим Так как , нулевая гипотеза не отклоняется. Рассмотрим теперь критерий со скорректированными степенями свободы. Имеем ; ; ; ; ; Окончательно имеем и . Рассчитаем критическое значение: Так как , нулевая гипотеза не отклоняется и в этом случае.