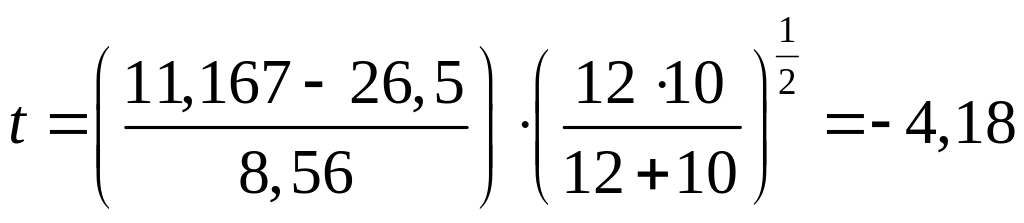- •Оглавление
- •Список используемых сокращений
- •Введение
- •Понятие и сущность статистических гипотез
- •1.1.Постановка проблемы
- •1.2. Статистический критерий
- •Классификация статистических критериев:
- •1.3. Функция потерь и критерий качества выбора решения
- •2. Проверка простой гипотезы против простой альтернативы
- •2.1. Вероятности правильных и ошибочных решений
- •Критерии принятия решений
- •Байесовское решение
- •Максимум апостериорной вероятности
- •Максимальное правдоподобие
- •Критерий Неймана-Пирсона
- •Минимаксное правило
- •Критерии значимости
- •3.1. Проверка гипотез для нормального распределения
- •3.1.1. Гипотезы о неизвестном среднем при известной дисперсии
- •3.1.2. Гипотезы о неизвестном среднем при неизвестной дисперсии
- •3.1.3. Гипотеза о неизвестной дисперсии
- •3.2. Сравнение средних нормального распределения
- •3.2.1. Проверка гипотез о равенстве средних для двух выборок
- •3.2.1.1. Гипотеза о равенстве средних при неизвестных равных дисперсиях
- •3.2.1.2. Гипотеза о равенстве средних при известных дисперсиях
- •3.2.1.3. Сравнение средних при неизвестных неравных дисперсиях
- •3.2.1.3.1. Критерий Кохрана-Кокса
- •3.2.1.3.2. Критерий Сатервайта
- •3.2.2. Проверка гипотез о равенстве средних для выборок
- •3.2.2.1. Критерий Полсона
- •3.2.2.2. Критерий Шеффе
- •3.3. Сравнение дисперсий нормального распределения
- •3.3.1. Проверка гипотез о равенстве дисперсий для двух выборок
- •3.3.1.1. Критерий Фишера
- •3.3.1.2. Критерий Романовского
- •3.3.2. Проверка гипотез о равенстве дисперсий для выборок
- •3.3.2.1. Критерии Бартлетта
- •3.3.2.2. Критерии Кохрена
- •3.3.2.3. Критерий Самиуддина
- •3.4. Проверка гипотез для экспоненциального распределения
- •3.4.1. Гипотеза о неизвестном параметре экспоненциального распределения
- •4. Общие критерии согласия
- •4.1.Критерии хи-квадрат Пирсона
- •4.2. Критерии хи-квадрат Фишера
- •4.3. Критерий согласия Колмогорова- Смирнова
- •4.4. Критерий Смирнова-Крамера-фон Мизеса
- •4.5. Критерий Андерсона-Дарлинга
- •4.6. Критерий согласим Дарбина
- •5. Частные критерии согласия
- •5.1. Критерии проверки нормальности распределения
- •5.1.1. Сравнительный анализ критериев нормальности
- •5.1.2. Критерий Шапиро-Уилка
- •5.1.3 Критерий
- •5.1.4 Критерий
- •5.1.5 Критерий
- •5.1.6. Критерий нормальности д'Агостино
- •5.1.7. Энтропийный критерий нормальности (критерий Васичека)
- •5.1.8. Критерий Дэвида-Хартли-Пирсона
- •5.2. Критерии проверки экспоненциальности распределения
- •5.2.1. Критерий Фроцини
- •5.2.2. Критерий Бартлетта-Морана
- •5.3. Критерии проверки равномерности распределения
- •5.3.1. Критерий Ченга – Спиринга
- •5.3.2. Критерий Саркади – Косика
- •5.4. Критерии симметрии
- •5.4.1. Критерий симметрии Смирнова
- •5.4.2. Одновыборочный критерий Вилкоксона
- •6. Критерии однородности
- •6.1. Критерий -квадрат
- •6.2. Критерий Колмогорова
- •6.3. Критерий Уилкоксона — Манна — Уитни
- •7. Подбор кривых распределения вероятностей по экспериментальным данным
- •7.1. Кривые Пирсона типа I
- •7.2. Кривые Пирсона типа II
- •7.3. Кривые Пирсона типа III
- •7.4. Кривые Пирсона типа IV
- •7.5. Кривые Пирсона типа V
- •7.6. Кривые Пирсона типа VI
- •7.7. Кривые Пирсона типа VII
- •Список используемой литературы
3.2. Сравнение средних нормального распределения
3.2.1. Проверка гипотез о равенстве средних для двух выборок
Проверяем
гипотезу
:
![]() .
Альтернативная
гипотеза
может
быть трех видов: а)
.
Альтернативная
гипотеза
может
быть трех видов: а)![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
Однако
случай в) сводится к случаю б) перестановкой
и
.
Однако
случай в) сводится к случаю б) перестановкой
и
![]() ,поэтому
не будет рассматриваться отдельно.
,поэтому
не будет рассматриваться отдельно.
3.2.1.1. Гипотеза о равенстве средних при неизвестных равных дисперсиях
Гипотеза
справедлива для любого
,
такого, что
![]() ,
т. е. гипотеза является сложной и может
быть сведена к простой, если рассматривать
разность средних
,
т. е. гипотеза является сложной и может
быть сведена к простой, если рассматривать
разность средних
![]() .
В этом случае естественно рассматривать
и разность оценок
.
В этом случае естественно рассматривать
и разность оценок
![]() ,
распределение которой нормальное,
поскольку нормальны
и
.
Для того чтобы нормировать разность
оценок, найдем ее дисперсию:
,
распределение которой нормальное,
поскольку нормальны
и
.
Для того чтобы нормировать разность
оценок, найдем ее дисперсию:
 .
.
Тогда
случайная величина
 .
.
Для оценки неизвестной дисперсии рассмотрим величины
 ,
,

которые
распределены по закону
с
и
![]() степенями свободы соответственно.
Следовательно, случайная величина
степенями свободы соответственно.
Следовательно, случайная величина
 - распределена по закону
с
- распределена по закону
с
![]() степенями свободы. Поскольку
степенями свободы. Поскольку
![]() ,
получаем
,
получаем

т.
е. случайная величина
 является несмещенной оценкой для
.
Поэтому величина
является несмещенной оценкой для
.
Поэтому величина
 (60)
(60)
где
 (61)
(61)
-
не зависит от неизвестных
![]() ,
,
![]() и
и распределена по закону Стьюдента с
степенями
свободы.
и
и распределена по закону Стьюдента с
степенями
свободы.
Эту же формулу можно представить в виде

Величина является объединенной оценкой дисперсии (общей для выборок).
Во всех случаях вычисляют статистику критерия:
 ,
где
,
где
Для проверки берутся критические точки распределения Стьюдента с степенью свободы и уровнем значимости , причем в случае а) - для двусторонней критической области, а в случае б) — для односторонней критической области.
В случае а), если , то гипотеза принимается, если - отвергается.
В случае б), если , то гипотеза принимается, если - отвергается.
Замечание:Поскольку для проверки гипотезы требуется равенство дисперсий для двух выборок, то вначале необходимо проверить это равенство. В противном случае данный метод применять нельзя.
Пример6
Имеются два ряда выборочных данных:
Необходимо
проверить гипотезу равенства средних
в обеих выборках
:
против
альтернативы
:
при
доверительной вероятности
Решение По формуле (39) находим:
По формуле (52) оценка дисперсии:
тогда используя формулу (61), получим:
Окончательно, наблюдаемое значение статистики определяемое формулой (60) имеет значение:
Из
табл. 3 для числа степеней свободы
|
3.2.1.2. Гипотеза о равенстве средних при известных дисперсиях
Проверяем гипотезу : . Альтернативная гипотеза может быть трех видов: а) , б) , в) , однако случай в) сводится к случаю б) перестановкой и и не будет рассматриваться отдельно. Во всех случаях вычисляют статистику критерия:
 (62)
(62)
В
случае а) критическая точка
![]() выбирается из условия
выбирается из условия
![]() .
Если
,
гипотеза
принимается, если
-
отвергается.
В случаях б) критическая точка
выбирается из условия
.
Если
,
то гипотеза
принимается,
если же
- отвергается.
.
Если
,
гипотеза
принимается, если
-
отвергается.
В случаях б) критическая точка
выбирается из условия
.
Если
,
то гипотеза
принимается,
если же
- отвергается.
Замечание:Гипотеза о средних проверяется таким образом обычно в случае больших выборок (объемом порядка сотен), когда оценки дисперсий можно принять за их точные значения.
Пример7
Имеются две выборки случайных величин:
с
известными дисперсиями
значений
:
Решение Вычисляем оценки средних, по формуле (39):
и статистику проверки нулевой гипотезы (62):
Для
имеем
(табл. 2) Так
как
|