Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Хабаровский государственный университет экономики и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5720.pdf

Скачиваний:

Добавлен:

13.11.2022

Размер:

6.42 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

Последнее уравнение запишем в виде				Это означает, что вершиной

является точка			.

Ответ:		– вершина параболы.

Пример 57.	Определить вид кривой заданной уравнением

Решение. Уравнение второй степени или соответствует равносторонняя гипербола, ветви которой лежат в первой и третьей четвертях при , а при − во второй и четвёртой четвертях. Оси координат являются

асимптотами такой гиперболы. В данном примере уравнение имеет вид

По правилу деления многочлена на многочлен, его можно преобразовать к виду

Ясно, что последнее уравнение будет задавать гиперболу, асимптотами которой будут прямые Так как то исходное уравнение имеет вид

и, следовательно, задаёт гиперболу	с вертикальной асимптотой		и
и, следовательно, задаёт гиперболу	с вертикальной асимптотой		и
горизонтальной асимптотой
Ответ: Гипербола с асимптотами		,
Ответ: Гипербола с асимптотами		,

Модуль 3. Элементы комплексного анализа

Пример 1. Указать действительную (вещественную) часть Re Z и мнимую часть

m Z следующих комплексных чисел:
1)	2)	3)	4)
1)	2)	3)	4)
Решение. Комплексное число есть число вида					где x и y	некоторые
Решение. Комплексное число есть число вида					где x и y	некоторые
					– так называемая мнимая единица,
действительные (вещественные) числа, а
действительные (вещественные) числа, а
т.е. число, квадрат которого равен (				1).
т.е. число, квадрат которого равен (				1).
			75

При этом

называется действительной (вещественной) частью комплексного числа

обозначается

(

), а y

его мнимой частью и обозначается

(

Обратимся к заданным числам. В первом случае

во

втором

Третье число

является действительным; так как его

можно записать в виде

Четвёртое мнимое число

можно записать в виде

и, следовательно,

Ответы: 1)

Пример 2.

Дать геометрическую интерпретацию следующим комплексным числам:

4) Z

Решение. В прямоугольной декартовой системе координат Oy на плоскости


произвольному комплексному числу			принято ставить в соответствие точку
M(x, y) или радиус-вектор		этой точки (известно, что		). Действительным
числам	(и только им)	будут соответствовать точки		оси абсцисс O (множество

действительных чисел есть подмножество комплексных чисел). Чисто мнимые числа (и только они) изображаются точками (0, y) оси координат Oy. В данным примере указанным комплексным числам будут соответствовать следующие

точки M(x, y) или радиусы-векторы

(5;2),

2) (3;

5),

3) (5; 0),

4) (0;

2).

Ответы: 1) (5;2), 2) (3;

5), 3) (5; 0),

4) (0;

2).

Пример 3.

Найти сопряжённое число

к числу

Решение. Комплексные числа Z

называются сопряженными.

Для данного

сопряжённым будет число

Ответ:

Найти сумму

Пример 4.

Решение. Сложение комплексных чисел

, a

определяется

равенством В связи геометрической интерпретацией комплексных чисел их сложение можно


рассматривать как сложение их радиусов векторов					и
Тогда в данном случае
Тогда в данном случае
Ответ:
Ответ:

Пример 5. Найти разность комплексных чисел и Решение. Разность определяется равенством

или как разность векторов		Тогда
или как разность векторов	76	Тогда
	76

Ответ:

Найти произведение комплексных чисел

Пример 6.

Решение.

Ответ можно получить по определению операции

умножения

на

т.е. по специальной формуле. Обычно умножение

на

проводят по правилу умножения суммы на сумму с учётом того, что

Поступая

так в данном примере, получим

Ответ:

Пример 7. Найти произведение

, если Z

Решение.

Легко установить, что

Так как в данном случае

Можно действовать по правилу примера 6. Тогда

Ответ:

Пример 8. Найти определитель квадратной матрицы

элементами которой являются комплексные числа.

Решение. Определитель матрицы второго порядка вычисляется по формуле

Тогда

Ответ:

Пример 9. Найти дробь

Решение. Имеется специальная формула для выполнения деления комплексных чисел, заданных в алгебраической форме. Ввиду её громоздкости проще действовать

так: числитель и знаменатель дроби

умножить на сопряжённое к знаменателю число

и с преобразованной так дробью (её числителем и знаменателем)

действовать по применённому в примере 6. правилу умножения. Тогда

и так

как

(см. пример

7), то останется найти

. Таким образом,

Ответ:

Пример 10. Указать модули и аргументы следующих комплексных чисел, записанных в тригонометрической форме:

Решение. Если точка	плоскости,	соответствующая комплексному числу
имеет полярные координаты		то число представлено в виде

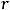называемом тригонометрической формой комплексного числа . При этом число (полярный радиус точки М) называется модулем комплексного числа и обозначается

Полярный угол

точки М называется аргументом числа и обозначается

Из данного примера имеем следующее:

Ответы: 1)

Пример 11. Записать в тригонометрической форме комплексное число

Решение. Пусть комплексное число

записано в тригонометрической

форме (см. решение предыдущего примера). Тогда

угол

определяется из равенств

При этом аргумент берут в

границах

В данном случае

Тогда

Для определения 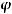имеем равенства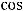 Следовательно, (это выписано так называемое главное значение аргумента). Таким образом,

тригонометрическая форма заданного числа имеет вид

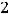
Ответ:

Пример 12. Найти геометрическое место точек комплексной плоскости, изображающих числа , удовлетворяющие следующим неравенствам:

1) , 2) 3) 4)

Решение. Так как


то	равносильно равенству			или	Это есть
окружность с центром в начале координат радиуса 4. Тогда ясно, что
	задаёт внутренность круга радиуса 4 с центром в начале координат, а
			этот же круг с его границей (контуром)		т.е. окружностью
			этот же круг с его границей (контуром)		т.е. окружностью
	В силу сказанного легко помнить, что неравенства				задают на
плоскости кольцо с внутренним контуром				(окружность радиуса 2) и внешним
контуром		(окружность радиуса 4). Читателю рекомендуется сделать рисунки.

Ответы:

1)Окружность радиуса 4 центром в начале координат; 2) Открытый круг радиуса 4

сцентром (0; 0); 3) Замкнутый круг радиуса 4 с центром (0; 0); 4) Кольцо.

Пример 13. Найти произведение комплексных чисел				и

Решение. Если и заданы в тригонометрической форме, то для их произведения справедливо равенство

т.е. при умножении чисел их модули перемножаются, а аргумент складывается. По

условию

Тогда

Ответ:

Пример 14. Найти

если

Решение. При делении

на

(при

заданных в тригонометрической

форме, справедливо равенство

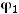
По условию, Тогда по выписанной формуле получим

Получен ответ в тригонометрической форме. Так как

то

алгебраической форме записи ответ будет таков:

Ответ:

Пример 15. Вычислить

Решение. Представим число

в тригонометрической

форме

воспользуемся формулой Муавра

Так как

Угол

найдём из равенства

. Следовательно,

Применив

формулу Муавра, получим

Ответ:

Пример 16. Вычислить вес значения корня 3-й степени из числа 1.

Решение. Если то при любом натуральном n имеет n значений, которые определяются формулой Муавра

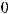
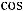
где Комплексное число в тригонометрической форме имеет вид Тогда все три значения даются формулой

Следовательно, значения таковы:

Ответ: Корнями являются числа

Пример 17. Записать в показательной форме комплексное число

Решение. Число заданные в тригонометрической форме, в силу формулы Эйлера +i sin записываются в виде называемой показательной формулой комплексного числа. Так как в данном примере


Ответ:

Пример 18. Комплексное число				заданное в показательной форме,
требуется записать в тригонометрической форме.

Решение. Число		в тригонометрической	форме имеет вид
	(см. предыдущий пример). Так как		в данном примере

Ответ:
Ответ: