
- •Кафедра математики и математических методов в экономике
- •ЛИНЕЙНАЯ АЛГЕБРА
- •Предисловие
- •Тестовые задания для самостоятельной работы
- •Тестовые задания с решениями
- •Модуль 1. Матричная алгебра
- •Модуль 2. Аналитическая геометрия
- •Модуль 3. Элементы комплексного анализа
- •Библиографический список
- •Содержание
- •ЛИНЕЙНАЯ АЛГЕБРА

Модуль 1. Матричная алгебра
Пример 1. Указать элемент  матрицы
матрицы
.
Выяснить размерность этой матрицы.
Решение. Элементы матрицы обычно обозначаются  . При этом индекс i означает номер строки, в которой находится этот элемент, а j − номер столбца. По условию
. При этом индекс i означает номер строки, в которой находится этот элемент, а j − номер столбца. По условию
требуется найти элемент |
|
, т.е. элемент, расположенный в третьей строке и втором |
|||||||||||||||||
столбце. Очевидно, что |
= − 4. Размерность матрицы, состоящей из m строк и n |
||||||||||||||||||
столбцов, |
обозначается |
|
|
. С |
учётом размерности |
матрицу записывают в виде |
|||||||||||||
. Данная матрица имеет три строки и четыре столбца. Следовательно, её |
|||||||||||||||||||
размерность есть |
|
. Матрицу можно записать так: |
. |
||||||||||||||||
Ответ: |
= − 4, |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Среди матриц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1) |
|
|
|
|
|
, 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
|
|
, |
4) |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
найти квадратную матрицу. Указать её порядок.
Решение. Квадратной называют матрицу, у которой m = n, т.е. число строк равно числу столбцов. Иногда такую матрицу записывают в виде  . Такой будет третья из выписанных матриц. Так как m = 3 и n = 3, то её размерность есть
. Такой будет третья из выписанных матриц. Так как m = 3 и n = 3, то её размерность есть 

 . Тогда говорят, что эта матрица есть матрица третьего порядка.
. Тогда говорят, что эта матрица есть матрица третьего порядка.
Ответ: Такой матрицей является матрица третьего порядка за номером 3).
Пример 3. Среди квадратных матриц выявить диагональную
1) |
|
|
|
|
|
|
|
, 2) |
, |
||
|
|
||||||||||
3) |
|
|
|
|
|
|
|
4) |
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Диагональной называют любую квадратную матрицу n-го порядка, все элементы которой вне главной диагонали (недиагональные элементы)  ,
,  , …,
, …,  равны нулю. При этом не обязательно, что все элементы главной диагонали отличны от нуля (среди них могут быть и равные нулю). У матрицы за номером 4)
равны нулю. При этом не обязательно, что все элементы главной диагонали отличны от нуля (среди них могут быть и равные нулю). У матрицы за номером 4)  = 2,
= 2,  =0,
=0,
20

 =4,
=4,  =5 (выписаны диагональные элементы), а остальные элементы равны нулю. Следовательно, она и является диагональной.
=5 (выписаны диагональные элементы), а остальные элементы равны нулю. Следовательно, она и является диагональной.
Ответ: Такой матрицей является квадратная матрица четвёртого порядка под номером 4).
Пример 4. Требуется выписать единичную матрицу третьего порядка.
Решение. Единичной матрицей называют диагональную матрицу n-го порядка, у которой все элементы главной диагонали равны единице ( =1, …,
=1, …,  =1).
=1).
Обозначают её E или . Таким образом, требуемая матрица имеет вид |
. |
Ответ:  =
= 

 .
.
|
Пример 5. Из квадратных матриц 1) |
|
|
|
, 2) |
, |
||
|
|
|||||||
3) |
, 4) |
|
|
|
выявить треугольную. |
|
||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Решение: Квадратная матрица называется треугольной, если все её элементы, расположенные по одну (любую) сторону от главной диагонали, равны нулю. Из выписанных такой матрицей является матрица под номером 4).
Ответ: 4).
Пример 6. Указать элемент  матрицы
матрицы  , являющейся транспонированной по
, являющейся транспонированной по
отношению к матрице = |
|
. |
||
|
|
|
|
|
Решение. Транспонированная матрица  получается из произвольной матрицы
получается из произвольной матрицы  путём размещения строк последней в соответствующие по номеру столбцы. Операция перехода от
путём размещения строк последней в соответствующие по номеру столбцы. Операция перехода от  к
к  называется транспонированием матрицы
называется транспонированием матрицы 
 Итак, транспонируя
Итак, транспонируя
получим |
= |
|
. Это и есть транспонированная матрица по отношению к |
заданной  . Элемент
. Элемент  матрицы
матрицы  расположен в её четвёртой строке и втором столбце. Очевидно, что
расположен в её четвёртой строке и втором столбце. Очевидно, что  = 7. Отметим, что матрица
= 7. Отметим, что матрица  имеет размерность
имеет размерность 

 , а её транспонированная имеет размерность
, а её транспонированная имеет размерность 

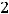 .
.
Ответ:  = 7.
= 7.
21

Пример 7. Найти элемент |
матрицы = |
|
, если она |
симметрична. |
|
|
|||||
Решение. Квадратная |
матрица называется |
|
симметричной, |
если |
= |
У симметричной матрицы элементы, расположенные симметрично относительно
главной диагонали, равны между собой ( |
= |
|
|
). Тогда |
= |
|
. Так как |
|
=5, то и |
||||||||||||
= 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
= 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 8. |
Найти элемент |
матрицы A+ |
B, если |
= 3, А = |
|
|
|
|
|
|
, |
||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В = |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение. Матрица С = В называется произведением матрицы В ( |
) |
любой |
|||||||||||||||||||
размерности |
|
на произвольное действительное число |
, |
если её элементы |
|||||||||||||||||
определяются равенством |
Тогда матрица |
имеет вид |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
= |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Сумма двух матриц А = |
и С = |
|
|
|
одинаковой размерности называется |
||||||||||||||||
|
|
|
|||||||||||||||||||
матрица D = A + C такой же размерности |
|
|
|
, элементы |
|
которой определяются |
|||||||||||||||
равенством |
|
|
. Следовательно, элементы матрицы А + |
|
С равны суммам |
||||||||||||||||
соответствующих элементов матриц А, С. Так как |
= |
3 и |
|
= |
|
|
3 (C = |
), то |
|||||||||||||
|
|
|
|||||||||||||||||||
|
= 3 |
|
3 =0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 9. Матрица А имеет размерность 4 |
3. Матрица В может иметь любую из |
||||||||||||||||||||
следующих размерностей: 1) 2 |
4, 2) 4 |
2, |
3)3 |
2, |
4) |
4 |
3. |
|
Выяснить, |
когда |
|||||||||||
возможно умножение матрицы А на матрицу В.
Решение. Умножение матрицы А на В возможно (тогда существует произведение А, важен порядок умножения), если число n столбцов матрицы А равно числу строк матрицы В. Так как размерность матрицы А есть 

 , то у неё три столбца (n = 3). Следовательно, среди матриц В надо искать ту, у которой число строк равно трём. Это есть третья матрица из 4 заданных.
, то у неё три столбца (n = 3). Следовательно, среди матриц В надо искать ту, у которой число строк равно трём. Это есть третья матрица из 4 заданных.
Ответ: 3), т.е. 
 .
.
Пример 10. Выяснить размерность матрицы АВ, если 
 ,
, 
 .
.
Решение. По условию матрица А имеет размерность 

 , т.е. у неё четыре строки и три столбца. (m = 4, n = 3); у матрицы В размерность
, т.е. у неё четыре строки и три столбца. (m = 4, n = 3); у матрицы В размерность 
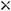
 (у неё три строки и два
(у неё три строки и два
22

столбца). Произведение АВ этих матриц возможно, т.к. число столбцов матрицы А равно числу строк матрицы В (об этих матрицах говорилось в примере 9). Размерность
матрицы АВ при заданных размерностях А и В определяется формулой |
|
|
|
|
||||||||||||||||||||||
, т.е. АВ имеет размерность |
. |
|
В |
данном |
примере |
|
|
|
а |
|||||||||||||||||
|
|
|
следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: Матрица АВ имеет размерность |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Пример |
11. Найти |
элемент |
матрицы |
С |
= |
АВ, |
если А = |
|
|
|
, |
|||||||||||||||
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В = |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Элементы |
матрицы С = ( |
, являющейся произведением матрицы |
|
|||||||||||||||||||||||
А = |
на матрицу В = |
, находятся по формуле |
|
|
|
|
||||||||||||||||||||
|
|
|
Формула означает, что элемент |
|
|
|
есть сумма попарных произведений |
|||||||||||||||||||
элементов i-й строки матрицы А и k-го столбца матрицы В. Т.к. находим элемент |
, |
|||||||||||||||||||||||||
то |
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Ответ: |
= 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример12. Выяснить возможность умножения матриц в следующих случаях: |
|
|||||||||||||||||||||||||
|
|
|
1) |
|
|
∙ |
|
|
; 2) |
|
|
∙ |
|
|
|
|
|
∙ |
; |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) |
|
|
|
|
5) |
|
|
|
|
|
|
|
6) |
∙ |
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Решение. Как отмечено при решении примера 9, умножение матриц возможно, если число столбцов первой матрицы равно числу строк второй матрицы, на которую первую умножают. Очевидно, что к таким ситуациям относят случаи: 2), 4), 5).
Ответ: Умножение возможно в случаях 2), 4), 5). |
|
|
|
|
|
|
|
|
|
|||||||||
Пример 13. |
Найти произведение АВ матриц А = |
|
|
, В = |
. |
|
|
|||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Размерность матрицы А есть |
|
, а В − |
|
|
. Т.к. |
число столбцов |
||||||||||||
матрицы А равно числу строк матрицы В, то умножение возможно. |
Выполним |
|||||||||||||||||
действие: АВ = |
|
|
∙ |
= |
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При умножении применялось правило указанное при решении примера 11. Получим
матрицу |
|
|
|
размерности |
. Отметим, что произведение ВА невозможно. |
|
|||||
Ответ: АВ = |
|
|
|
||
|
|
|
|||
23

Пример 14. Найти произведения АВ и ВА матриц А = |
, В = |
. |
Решение. Произведение АВ существует, т.к. А имеет размерность 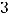

 , а В
, а В 


 . Применяем правило, которое было указанно в примере 11.
. Применяем правило, которое было указанно в примере 11.
.
Получилась матрица размерности 
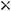
 , т.к.
, т.к. 
 , а
, а 
 , то произведение ВА также
, то произведение ВА также
возможно. Проведём действие: ВА = |
|
. |
|
ВА имеет размерность 

 , т.е. есть квадратная матрица первого порядка.
, т.е. есть квадратная матрица первого порядка.
Ответ: АВ = |
|
|
|
|
|
, ВА = (9). |
|
|
|
Пример 15. Найти матрицы  и
и 
 , если А=
, если А= 


 и
и  единичная
единичная
матрица третьего порядка.
Решение. Непосредственно по определению умножения матриц легко установить, что  = А и
= А и 
 = А.
= А.
Ответ: 


 =А.
=А.
Пример 16. Пусть существует произведение АВ блочных матриц.
А = |
|
|
|
, В = |
|
|
. Размерность блоков [ |
|
|
|
а блоков |
|||||||
|
|
|
||||||||||||||||
|
|
|
|
|
Требуется найти число строк в блоках |
, |
, если |
даны |
||||||||||
|
|
|
|
|||||||||||||||
следующие варианты ответов: |
|
|
|
|
|
|
|
|
|
|||||||||
1) |
|
1-я строка, |
|
2-я строка; 2) |
– 3-я строка, |
|
1 строка; 3) |
|
2-я |
|||||||||
|
|
|
|
|||||||||||||||
строка, |
|
|
|
2-я строка;4) |
|
|
3-я строка, |
|
|
2-я строка. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение. По условию задачи матрица А имеет вид А = |
. |
|
|
|
|
|||||||||||||
В этой записи, элементы отмечены точками, блоки разделены (размерности блоков указаны в задаче). Очевидно, что матрица А имеет 5 столбцов. Т.к. АВ существует, то у матрицы В должно быть 5 строк. Т.к. блоки  ,
,  расположены один под другим, то из предложенных вариантов этому условию (5 строк у матрицы В) удовлетворяет только вариант 4. Конечно, число строк в блоках
расположены один под другим, то из предложенных вариантов этому условию (5 строк у матрицы В) удовлетворяет только вариант 4. Конечно, число строк в блоках 
 может быть другим, но общее их число 5 (количество столбцов во всех блоках)
может быть другим, но общее их число 5 (количество столбцов во всех блоках)  не играет роли).
не играет роли).
Ответ: Из предложенных вариантов подходит вариант 4).
24

Пример 17. Выяснить, в какую точку преобразуется точка М (5,1) двумерного арифметического пространства с помощью линейного преобразования У=АХ с
матрицей А = |
. |
Решение. В подробной записи линейное преобразование имеет вид:
Подставив координаты 

 ,
, 

 точки М в эти равенства, получим
точки М в эти равенства, получим 









 ,
, 







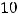 . Таким образом точка м(5,1) перейдёт в точку
. Таким образом точка м(5,1) перейдёт в точку  (13,10) в декартовой системе координат 0
(13,10) в декартовой системе координат 0
 .
.
Ответ:  (13,10).
(13,10).
Пример 18. Вычислить определитель матрицы. А = .
Решение. Заданная матрица есть квадратная матрица второго порядка.
Определитель (детерминант) квадратной матрицы. А = |
|
второго порядка |
||
проще всего вычислить по формуле |
= |
|
|
, т.е. |
|
|
|||
от произведения диагональных элементов надо вычесть произведение элементов второй (лобочной) диагонали матрицы. В формуле слева даны различные обозначения определителей. В рассматриваемом примере 

 ,
, 

 ,
, 


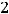 ,
, 

 . Тогда
. Тогда
= 1∙6 ( 2)∙3 = 12.
Ответ: ∆ (А) = 12. |
|
|
Пример 19. Найти элемент |
матрицы А = |
, если ∆ (А) = 3. |
Решение. Вычислим определитель матрицы А по правилу, указанному при решении примера 18. Получим:
Т.к. по условию ∆ (А) = 3, то элемент  находится из равенства
находится из равенства 




 или
или 



 . Следовательно,
. Следовательно, 


 . Легко проверить, что при
. Легко проверить, что при 


 будет
будет
равенство ∆ (А) = 3. Действительно, |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
Ответ: 


 .
.
Пример 20. Вычислить определитель
25

третьего порядка методом разложения по какой нибудь его строке или какомунибудь его столбцу 9 по правилу Лапласа).
Решение. Этот определитель можно вычислить и другими способами ( например, по правилу треугольника или методам Гаусса). Правило Лапласа можно применять для определителей любого порядка 

 . При этом определитель можно вычислять разложением по любой строке (любому столбцу). Если разлагаем по первой строке, то формула вычисления определителя n-го порядка имеет вид
. При этом определитель можно вычислять разложением по любой строке (любому столбцу). Если разлагаем по первой строке, то формула вычисления определителя n-го порядка имеет вид
.
В случае определителей второго порядка справа в этой формуле будут два слагаемых, а в случае определителей третьего порядка три слагаемых. Аналогичные
формулы имеют место для остальных строк и |
всех столбцов. Элементы |
|
это |
|||||||
|
||||||||||
алгебраическое дополнение |
элементов |
соответствующей |
матрицы. |
Они |
||||||
вычисляются по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
− миноры элементов |
. Миноры |
элементов |
|
|
это определители |
||||
|
||||||||||
(n 1) – го порядка, полученные из элементов матрицы А, оставшихся после вычёркивания i-й строки и j-го столбца (без изменения порядка элементов). Из
формулы для алгебраических дополнений следует, что |
, если i+j |
|
число |
||
|
|||||
чётное, и |
|
, если сумма i+j есть число нечётное. |
|
|
|
|
|
|
|
||
Проведём вычисления алгебраических дополнений в случае матрицы данного
примера: |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Тогда при разложении по первой строке получим |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Такой же результат получим при разложении по двум другим строкам. Вычислим этот же определитель разложением по первому столбцу:





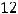 .
.
Тот же результат получим при разложении этого определителя по двум другим столбцам.
Ответ: 

 .
.
26

Пример 21. Вычислить определитель
 .
.
Решение. Воспользуемся правилом Лапласа. Для уменьшения вычислительной работы разлагать надо по той строке (тому столбцу), где имеется больше всего нулей. Следовательно, надо разлагать по третьему столбцу. Тогда:

 .
.
Ответ: 

 .
.
Пример 22. Определитель
Вычисляется разложением по второй строке. Выяснить, какой из вариантов ответов
1) 


2) 

3) 

4) |
|
|
|
|
|
. |
|
является правильным.
Решение. Разложение по второй строке имеет вид:






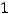

 .
.
Вычисли участвующие здесь алгебраические дополнения:
,
,
.
Тогда
,
т.е. правильный ответ – это вариант 3). Ответ: Вариант 3), при этом 


 .
.
27

Пример 23. Вычислить определитель |
|
матрицы |
||
|
|
|
|
|
|
|
|
. |
|
Решение. Если матрица n-го порядка является матрицей треугольного вида, то её
определитель равен произведению диагональных элементов, т.е. |
. |
||||||||||||
В данном примере |
|
|
|
|
|
|
|
|
, |
. |
|
||
|
|
|
|
||||||||||
Тогда |
|
|
. |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: |
|
|
|
|
|
|
|
|
|
|
|||
Пример 24. Вычислить определитель |
|
|
методом Гаусса. |
|
|||||||||
|
|
||||||||||||
Решение: Будем преобразовывать этот определитель, пока не получим определитель с матрицей треугольного вида, который, как отмечено выше, равен произведению диагональных элементов. При этом каждый раз будем помечать разрешающий элемент 

 . Описание метода Гаусса см., например, в [6, 8, 10].
. Описание метода Гаусса см., например, в [6, 8, 10].
Метод основан на следующем свойстве: определитель не изменится, если к элементам какой-нибудь строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число. Свойство относится и к столбцам определителя. На первом этапе преобразования элементы разрешающей строки S остаются неизменными.
Все элементы разрешающего k-го столбца, |
кроме разрешающего |
элемента |
, |
заполняются нулями. Остальные элементы |
нового определителя, |
заполняющие |
|
места элементов , вычисляются по правилу треугольника, т.е. по формуле |
|
||

 .
.
Новый определитель надо вычислит путем разложения по элементам разрешающего столбца. Придётся вычислить минор 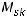 элемента
элемента  , который будет определителем меньшего (n-1)-го порядка. С этим определителем проводится аналогичная процедура и т.д. При этом на последующих шагах (этапах) разрешающие строки остаются неизменными. В результате таких действий с данным определителем имеем:
, который будет определителем меньшего (n-1)-го порядка. С этим определителем проводится аналогичная процедура и т.д. При этом на последующих шагах (этапах) разрешающие строки остаются неизменными. В результате таких действий с данным определителем имеем:

 .
.
Ответ: 


 .
.
28

Пример 25. Определитель
вычисляется методом Гаусса. Выяснить, в каком из случаев
,
преобразования приведены правильно. Указать значение определителя.
Решение. За разрешающий элемент взят элемент 



 . В следующей записи первая строка остаётся неизменной, а первый столбец, кроме элемента
. В следующей записи первая строка остаётся неизменной, а первый столбец, кроме элемента 

 , дополняется нулями. Это сделано правильно в каждом случае. Остальные элементы вычисляются по правилу прямоугольника. Это сделано правильно во втором случае. При этом определитель свёлся к определителю с матрицей треугольного вида. Следовательно
, дополняется нулями. Это сделано правильно в каждом случае. Остальные элементы вычисляются по правилу прямоугольника. Это сделано правильно во втором случае. При этом определитель свёлся к определителю с матрицей треугольного вида. Следовательно 







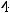



Ответ: Преобразования проведены верно в случае 2, при этом ∆ = 24.
Пример 26. Установить, при какой λ выполняется равенство
Решение. Очевидно, что указанное равенство выполняется при 

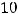
 При таком λ третья строка будет пропорциональна второй. Известно свойство: определитель, у которого какие-нибудь две строки пропорциональны, равен нулю.
При таком λ третья строка будет пропорциональна второй. Известно свойство: определитель, у которого какие-нибудь две строки пропорциональны, равен нулю.
Ответ: λ=10.
Пример 27. Вычислить, какая из матриц имеет обратную |
|
. |
|
Решение. Для квадратной матрицы  существует единственная обратная матрица
существует единственная обратная матрица 

 если
если 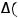


 , т.е. определитель матрицы
, т.е. определитель матрицы  отличен от нуля. Очевидно, что в случаях 1), 2) и 4)
отличен от нуля. Очевидно, что в случаях 1), 2) и 4) 


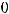 . В случае 3)
. В случае 3) 


 . Действительно,
. Действительно,
Таким образом, в случае 3) существует 



29

Ответ: Случай 3), |
. |
Пример 28. Установить, при каком λ матрица 
не имеет обратной.
Решение. Матрица  не имеет обратной, если она является вырожденной (особенной), т.е. в случае
не имеет обратной, если она является вырожденной (особенной), т.е. в случае 


 (см. предыдущий пример). Тогда должно выполняться равенство
(см. предыдущий пример). Тогда должно выполняться равенство
т.е. 2 λ – 12 = 0. Тогда λ = 6.
Ответ: при λ = 6 данная матрица не имеет обратной.
Пример 29. Указать, какая из матриц
,
является обратной к матрице |
|
|
|
|
||
|
|
|
|
|
|
|
. |
|
|
|
|
||
Решение. Для обратной матрицы справедливы равенства |
|
|
|
где |
||
|
|
|||||
Е – единичная матрица того же порядка, что и квадратная матрица А. Таким образом, надо проверить эти равенства. Согласно правилу умножения матриц, это будет только в случае 3). Действительно,
Остальные случаи читатель может проверить самостоятельно. Ответ: матрица случая 3).
Пример 30. Найти обратную матрицу к матрице
.
30

Решение. Если 


 , то существует единственная обратная матрица в матрице A, которая имеет вид
, то существует единственная обратная матрица в матрице A, которая имеет вид
Заметим, что алгебраические дополнения  строк матрицы А являются её обратной матрицей. Вычислим определитель матрицы А:
строк матрицы А являются её обратной матрицей. Вычислим определитель матрицы А:











 .
.
Теперь найдём алгебраические дополнения |
|
(см. пример 20 об их нахождении): |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В этих равенствах участвовали определители первого порядка, которые равны самим элементам 



 символ
символ  означает определитель матрицы
означает определитель матрицы  , а не модуль числа
, а не модуль числа 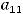 ). Согласно указанной формуле имеем
). Согласно указанной формуле имеем
Легко проверить, что равенство 








 выполняется. Например,
выполняется. Например,
Ответ:




 .
.
Пример 31. Опираясь на определение ранга матрицы с помощь понятия её миноров, найти ранги следующих матриц:
Решение. Определитель k-го порядка, составленный из элементов матрицы А размерности 








 расположенных на пересечении любых выделенных k строк и k столбцов, называется минором k-го порядка этой матрицы и обозначается
расположенных на пересечении любых выделенных k строк и k столбцов, называется минором k-го порядка этой матрицы и обозначается  .
.
31

Рангом матрицы называется наивысший порядок отличных от нуля миноров, порождённых этой матрицей.
Ранг нулевой матрицы любо размерности, по определению, полагается равным нулю.
Ранг матрицы А обозначается 


 или просто r. Из сказанного ранее следует, что ранг любой ненулевой матрицы удовлетворяет неравенством
или просто r. Из сказанного ранее следует, что ранг любой ненулевой матрицы удовлетворяет неравенством
Только нулевая матрица имеет ранг, равный нулю.
Все матрицы этого примера не являются нулевыми. Поэтому их ранги удовлетворяют неравенству 


 Минорами высшего порядка первых двух матриц являются миноры второго порядка. Поэтому их ранги удовлетворяют неравенству
Минорами высшего порядка первых двух матриц являются миноры второго порядка. Поэтому их ранги удовлетворяют неравенству 


 Следовательно, ранги этих матриц равны либо единице, либо двум.
Следовательно, ранги этих матриц равны либо единице, либо двум.
Единственный минор второго (высшего) порядка матрицы |
|
равен |
|||
нулю. Тогда |
|
|
|
|
|
Отметим, что все миноры |
первого порядка |
(это сами элементы этой матрицы) |
|||
отличны от нуля. Единственный минор второго (высшего) порядка матрицы |
|
||||
также равен нулю. Поэтому |
. Эта матрица имеет один минор |
||||
первого порядка |
, не равный нулю, т.е. матрица не является нулевой. |
||||
Следовательно, |
Минорами высшего порядка матриц |
и |
является |
||
миноры второго порядка, |
поэтому их ранги удовлетворяют неравенству |
Обе |
|||
матрицы имеют по три минора второго порядка. У матрицы  они таковы:
они таковы:
Так как имеются отличные от нуля миноры второго (высшего) порядка, отличные от нуля, то 


 . У матрицы
. У матрицы  миноры второго порядка таковы:
миноры второго порядка таковы:
т.е. все равны нулю. Тогда 


 и её ранг либо 0, либо 1. Так как она ненулевая, то
и её ранг либо 0, либо 1. Так как она ненулевая, то
Минорами высшего порядка матриц  и
и  являются миноры третьего порядка. Тогда ранги этих матриц удовлетворяют неравенству
являются миноры третьего порядка. Тогда ранги этих матриц удовлетворяют неравенству 


 Единственный минор третьего порядка матрицы
Единственный минор третьего порядка матрицы 
отличен от нуля. Следовательно, |
|
Единственный минор третьего порядка матрицы |
равен нулю. Действительно, |
различая его по первому столбцу, получим |
|
32 |
|

Тогда нужно обратиться к минорам второго порядка этой матрицы. Например, её
угловой минор |
отличен от нуля. Сразу заключаем, что |
. |
||
Ответы: |
|
|
|
|
Замечание. Для квадратной матрицы |
n-ого порядка справедливо следующее |
|||
утверждение: |
тогда и только |
тогда, когда |
(матрица |
– |
невырожденная). Это утверждение состоит из прямого и обратного. Оно очевидно образом следует из определения ранга матрицы. Тогда справедливы и утверждения:
1) |
если |
, то |
(тогда |
; |
2) |
если |
, то |
|
|
Естественно, |
что при |
тестировании |
могут быть задания, связанные с этими |
|
простыми утверждениями. Этим замечанием можно было воспользоваться при
вычислении рангов матриц и |
из предыдущего примера 31. Действительно, |
|||
Тогда |
( |
и |
( |
. Тогда как обе матрицы |
ненулевые |
(тогда |
), |
то их |
ранги равны единице. Ранее это |
утверждение было сделано на основании определения ранга матрицы.
Пример 32. Найти ранги квадратных матриц
Решение. Очевидно, что 




 ,
, 

Согласно замечанию 


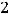



 .
.
Ответы: 






 .
.
Пример 33. Найти ранги матриц
с помощью элементарных преобразований.
33

Решение. По поводу определения элементарных преобразований матрицы надо обратиться, например, к [6, 8, 10].
Справедлива теорема: при элементарных преобразованиях матрицы её ранг не изменяется.
Матрицы, полученные одна из другой с помощью элементарных преобразований, называются эквивалентными. Эквивалентность двух матриц А и В записывают так: 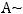
 . Эквивалентные матрицы имеют равные ранги.
. Эквивалентные матрицы имеют равные ранги.
На элементарных преобразованиях основан способ вычисления ранга матрицы. Именно данную матрицу преобразуют к эквивалентной, у которой без труда можно заметить так называемый ранговый минор  . Обычно, отбрасывая нулевые строки и столбцы, матрицу приводят к трапецеидальной или треугольной форме. Этот способ особенно полезен в случае больших размерностей матриц. Преобразования над матрицей будут напоминать действия, проводившиеся при вычислении определителей методом Гаусса (см. примеры 24, 25). При этом будет применяться упоминавшееся там правило прямоугольника для пересчёта элементов.
. Обычно, отбрасывая нулевые строки и столбцы, матрицу приводят к трапецеидальной или треугольной форме. Этот способ особенно полезен в случае больших размерностей матриц. Преобразования над матрицей будут напоминать действия, проводившиеся при вычислении определителей методом Гаусса (см. примеры 24, 25). При этом будет применяться упоминавшееся там правило прямоугольника для пересчёта элементов.
В результате действий над матрицей А получим следующие эквивалентности:
Матрица 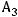
 преобразовалась к эквивалентной матрице трапецеидальной формы размерности
преобразовалась к эквивалентной матрице трапецеидальной формы размерности 

 . За ранговый минор последней матрицы можно взять минор
. За ранговый минор последней матрицы можно взять минор


 , отличный от нуля. Следовательно, её ранг равен двум, тогда и
, отличный от нуля. Следовательно, её ранг равен двум, тогда и
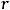


 ( в силу теоремы о сохранении ранга при элементарных преобразованиях). Проведём элементраные преобразования над матрицей В:
( в силу теоремы о сохранении ранга при элементарных преобразованиях). Проведём элементраные преобразования над матрицей В:
Очевидно, что последняя матрица имеет треугольную форму. Её единственный минор высшего (четвёртого) порядка
отличен от нуля. Ранг этой матрицы равен четырём. Тогда 


 .
.
Ответы: 


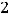 ,
, 


 .
.
34

Пример 34. Выяснить, какая из матриц
1) |
|
, 2) |
|
|
, |
||
|
|
||||||
3) |
, 4) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||
является расширенной матрицей соответствующей из систем
1) |
|
2) |
|
линейных алгебраических уравнений.
Решение. Если линейная система имеет вид
то матрица |
из коэффициентов при неизвестных |
называется |
матрицей системы, а матрица  =
=
называется расширенной матрицей этой системы. Матрица  по сравнению с А имеет один дополнительный столбец, элементами которого являются правые части системы.
по сравнению с А имеет один дополнительный столбец, элементами которого являются правые части системы.
Расширенная матрица  имеет размерность
имеет размерность 

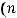

 .
.
Согласно сказанному, системе 1) соответствует её расширенная матрица
,
которая в условии примера выписана под номером 2).
Очевидно, что у система 2) расширенной матрицей является матрица под номером 4). Выписанные матрицы 1) и 3) к данным системам не имеют никакого отношения.
Ответы: Системе 1) соответствует её расширенная матрица под номером 2), а системе 2) – матрица под номером 4).
Пример 35. Установить, какой из векторов
1) (1, –2, 5), 2) (2,4), 3) (2, –2, 3), 4) (–2, 1, 3, 5)
является решением системы
линейных алгебраических уравнений.
35

Решение. Решением линейной системы алгебраических уравнений с неизвестными 

 называется такая упорядоченная совокупность из n чисел
называется такая упорядоченная совокупность из n чисел 

 , что каждое из уравнений системы обращается в тождество после замены неизвестных
, что каждое из уравнений системы обращается в тождество после замены неизвестных 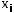 соответствующими числами
соответствующими числами 




 . Вектор (
. Вектор (

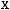 ), координатами которого
), координатами которого
является n-мерным вектором. Его можно рассматривать, как матрицу – строку
размерности |
. При транспонировании записывают его в виде |
|
||
|
|
|
, |
|
т.е. в виде матрицы-столбца размерности |
. Тогда неизвестные решения системы |
|||
можно трактовать как векторы |
или матрицы-столбцы X. Конкретные |
же решения |
||
есть n-мерные векторы |
. |
|
|
|
Рассматриваемая система есть система |
с тремя неизвестными |
. Тогда |
||
решениями могут быть только трехмерные векторы. Ответы 2) и 4) отпадают, т.к. один вектор является двумерным, а второй – четырёхмерным. Остаётся проверить векторы 1)
и 3).
При подстановке координат первого вектора (1; –2; 5) в первое уравнение системы получится тождество 3 = 3, а при их подстановке во второе и третье уравнения системы получаются противоречивые равенства. Таким образом, вектор (1; –2; 5) не есть
решение данной системы. Легко проверить, что координаты третьего вектора |
(2; –2; |
|||||
3) обращают все три равенства системы в тождества: |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, решением системы является вектор (2;−2; 3).
Ответ: Вектор 3), т.е. вектор (2; –2; 3).
Замечание. Важнейшей задачей линейной алгебры является исследование систем линейных алгебраических уравнений. (см.[2, 6, 8, 10]).
Она состоит в том, чтобы установить, совместна система или нет, а в случае совместимости указать число решений и методы их нахождения.
При это возможна одна из следующих ситуаций:
1)система несовместна или противоречива, т.е. решений нет;
2)система совместна и определена, т.е. имеет единственное решение;
3)система совместна, но является неопределенной, т.е. имеет бесчисленное множество решений.
Исследование на совместность можно провести двумя способами:
36

1)методом последовательного исключения неизвестных (методом Гаусса) или методом полного исключения неизвестных (методом Гаусса-Жордана);
2)методом сравнения рангов матрицы системы и её расширенной матрицы.
При методе Гаусса применяются элементарные преобразования системы. Элементарными преобразованиями системы линейных уравнений называются
следующие преобразования:
1)перестановка местами любых двух уравнений системы;
2)умножение любого уравнения системы на отличное от нуля число;
3)прибавление к любому уравнению системы всякого её другого уравнения, умноженного на некоторое число.
Отметим следующее. Преобразование третьего вида применялось при вычислении определителей методом Гаусса. Элементарным преобразованиями системы линейных уравнений соответствуют элементарные преобразования строк расширенной матрицы  этой системы. Элементарные преобразования матриц (к ним относятся ещё аналогичные преобразования над столбцами матрицы) применялись в примере 33 при вычислении рангов матриц.
этой системы. Элементарные преобразования матриц (к ним относятся ещё аналогичные преобразования над столбцами матрицы) применялись в примере 33 при вычислении рангов матриц.
Справедлива теорема: при элементарных преобразованиях система линейных уравнений переходит в равносильную ей систему.
Напомним, что две системы линейных алгебраических уравнений с одними и теми же неизвестными называются равносильными (эквивалентными), если они либо обе несовместны, либо обе совместны и обладают одними и теми же решениями.
При элементарных преобразованиях с системой в новой системе может появиться
одно или несколько уравнений вида |
. |
|
При |
последнее уравнение противоречиво, |
тогда противоречива и исходная |
система. При свободном члене b = 0 такие уравнения из системы исключаются (в новой системе будет меньше уравнений).
С помощью элементарных преобразований (методом Гаусса) исходную систему можно привести к треугольному или трапецеидальному виду (возможно, после перестановки местами некоторых уравнений или (и) соответствующей перенумерации неизвестных (см. примеры в [6, 8]).
В случае треугольного вида новой системы решение будет только одно, а в случае трапецеидального вида − бесчисленное множество.
При исследовании систем с помощью ранга применяются следующие теоремы (критерии совместности и определенности системы).
Теорема 1 (Кронекера − Капелли). Система линейных уравнений совместна тогда и только тогда, когда выполняется равенство


 .
.
Последнее равенство означает, что ранг матрицы А системы равен рангу расширенной
матрицы этой системы. Заметим, что всегда либо |
= |
, либо |
= |
. |
37 |
|
|
|
|

В последнем случае 



 система противоречива.
система противоречива.
Теорема 2. В случае совместной системы ( |
) справедливы |
утверждения:
1.Если r = n, то система имеет единственное решение (определена).
2.Если r  n, то система имеет бесчисленное множество решений.
n, то система имеет бесчисленное множество решений.
Теоремы 1 и 2 позволяют исследовать систему. Само же решение таким путём не получим.
Проиллюстрируем примерами все положения и выводы этого замечания.
Пример 36. Выяснить, является ли совместной система линейных уравнений с тремя переменными, если при её исследовании методом Гаусса получилось уравнение












 .
.
Решение. Полученное уравнение противоречиво, т.к. при любом наборе неизвестных 

 его левая часть обращается в нуль, а правая часть нулю не равна. Преобразованная система будет противоречивой и по равносильности систем заключаем, что и исходная система противоречива.
его левая часть обращается в нуль, а правая часть нулю не равна. Преобразованная система будет противоречивой и по равносильности систем заключаем, что и исходная система противоречива.
Ответ: система противоречива (решение нет).
Пример 37. Исследовать систему которая с помощью метода Гаусса привилась к виду
Решение. Переставив в этой системе местами второе и третье уравнения, получим следующую систему треугольного вида:
Последняя система имеет только одно решение, которое находится обратным ходом
метода Гаусса. Из третьего уравнения получаем, что |
|
. Подставив |
во второе |
||||||||||||
|
|||||||||||||||
уравнение, получим |
|
|
, |
, =4. Теперь подставим найденные |
|||||||||||
|
|||||||||||||||
|
|
|
в |
первое |
уравнение. Получим следующее: |
|
|
|
, |
||||||
|
|
|
|
|
|||||||||||
, |
|
|
|
|
, |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Единственное решение системы можно записать в виде (−3; 4; −2), т.е. в виде трёхмерного вектора.
Ответ: Единственное решение таково: ( 3; 4; 2).
Сделаем замечание к примеру. Расширенная матрица полученной треугольной системы имеет вид
38

.
Матрица А системы (её элементы расположены левее вертикальной черты) является треугольной. Тогда ∆(А) = 2∙4∙(−5) = −40  0. Единственный минор третьего (высшего) порядка этой матрицы совпадает с её определителем:
0. Единственный минор третьего (высшего) порядка этой матрицы совпадает с её определителем: 







 . Следовательно, r(A). Этот же минор будет одним из четырёх миноров третьего (высшего) порядка матрицы
. Следовательно, r(A). Этот же минор будет одним из четырёх миноров третьего (высшего) порядка матрицы  . Тогда r(
. Тогда r( = 3. Получилось, что r(A) = r(
= 3. Получилось, что r(A) = r( . Выполнено условие по теореме Кронекера − Капелли, система совместна. Число n неизвестных системы также равно трём, т.е. r = n. Из приведённой в замечании теоремы 2 вытекает, что решение треугольной системы единственно. Решение используемой исходной системы также будет единственным. Исследование проведено, но оно само таким путём не получено. Метод же Гаусса позволяет не только исследовать систему, но и получить её решения.
. Выполнено условие по теореме Кронекера − Капелли, система совместна. Число n неизвестных системы также равно трём, т.е. r = n. Из приведённой в замечании теоремы 2 вытекает, что решение треугольной системы единственно. Решение используемой исходной системы также будет единственным. Исследование проведено, но оно само таким путём не получено. Метод же Гаусса позволяет не только исследовать систему, но и получить её решения.
Пример 38. Исследовать методом Гаусса систему
с тремя уравнениями и четырьмя неизвестными.
Решение. Заполняем таблицу Гаусса и проводим итерации (этапы, шаги).
|
|
|
|
|
|
1 |
-1 |
-1 |
5 |
1 |
2 |
1 |
2 |
2 |
4 |
2 |
-2 |
-2 |
10 |
|
|
|
|
|
2 |
1 |
-1 |
-1 |
5 |
0 |
3/2 |
3/2 |
5/2 |
-1/2 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
За разрешающий элемент взяли элемент 

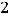

 , отмеченный в исходной таблице. Первая (разрешающая) строка в новую таблицу переносится без изменений. Разрешающий первый столбец преобразуется. В первом столбце новой таблицы разрешающий элемент сохраняется, а остальные элементы заполняются нулями. Это означает, что в последующих после первого уравнениях преобразованной системы исключена переменная x1. Остальные элементы второй таблицы вычислялись по правилу прямоугольника, уже применявшемся при вычислении определителей методом Гаусса и при нахождении рангов матриц методом элементарных преобразований (см.
, отмеченный в исходной таблице. Первая (разрешающая) строка в новую таблицу переносится без изменений. Разрешающий первый столбец преобразуется. В первом столбце новой таблицы разрешающий элемент сохраняется, а остальные элементы заполняются нулями. Это означает, что в последующих после первого уравнениях преобразованной системы исключена переменная x1. Остальные элементы второй таблицы вычислялись по правилу прямоугольника, уже применявшемся при вычислении определителей методом Гаусса и при нахождении рангов матриц методом элементарных преобразований (см.
примеры 24, 25, 33).
Выполнена только одна итерация, и уже можно сделать вывод. Из второй таблицы видно, что третье уравнение преобразованной системы имеет вид


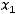













 .
.
39

Оно возможно при любых значениях этих четырёх неизвестных и его надо исключить из системы. Останется следующая система из двух уравнений:
которая имеет трапецеидальный вид. Следовательно, эта и исходная системы имеют бесконечное множество решений.
Покажем ещё, как найти все решения системы. Для этого в последней системе из двух уравнений члены с неизвестными  и
и  перенесём в первую часть системы; получим
перенесём в первую часть системы; получим
Из второго уравнения этой системы переменная  выразится через
выразится через  и
и  . Это выражение для
. Это выражение для 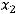 подставим в первое уравнение и после этого найдём, как выражается
подставим в первое уравнение и после этого найдём, как выражается  через
через  и
и  . В результате таких действий имеем
. В результате таких действий имеем
Это получено так называемое общее решение системы. Из него можно получить любые частные решения из бесконечного множества решений. Для этого каждый раз свободным (параметрическим) переменным 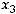 и
и  надо придать произвольные, но фиксированные значения. После этого найдутся свои конкретные значения основных (базисных) неизвестных
надо придать произвольные, но фиксированные значения. После этого найдутся свои конкретные значения основных (базисных) неизвестных 

 Например, если
Например, если 

 ,
, 


 , то из системы получим
, то из системы получим
|
, |
|
; одно частное решение таково: ( |
|
; |
|
; 1; −1). Если |
и |
, то |
|
|
|
|


 ,
, 




В этом случае частное решения таково: ( ; −
; − 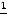 ; 0; 0). Последнее есть так называемое
; 0; 0). Последнее есть так называемое
базисное решение системы.
Ответ: Система совместна и неопределенна, т.е. имеет бесконечное множество решений.
Рекомендуем провести исследование системы из примера 38 с помощью теорем 1 и 2. Для этого проще всего обратиться к полученной при решении этого примера таблице, провести сравнение рангов матриц системы, сравнить ранг с числом неизвестных (при условии совместности системы). Напоминаем, что ответ должен получиться прежним.
Пример 39. Исследовать методом Гаусса систему уравнений.
40

Решение. Заполняем таблицу Гаусса и проводим итерации.
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
-2 |
|
1 |
1 |
2 |
-1 |
|
|
|
|
|
2 |
|
3 |
18 |
0 |
-1 |
|
|
|
|
|
2 |
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
-2 |
|
1 |
1 |
0 |
|
|
|
|
|
|
6 |
|
1 |
16 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
0 |
-1 |
|
|
|
|
|
2 |
|
2 |
4 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
-2 |
|
1 |
1 |
0 |
-3 |
|
|
|
|
|
6 |
|
1 |
16 |
0 |
0 |
|
|
|
|
|
0 |
|
5/3 |
-4/3 |
|
|
|
|
|
|
|
|
|
|
|
Из последней таблицы видно, что |
|
и поэтому преобразованная система не |
||||||||
является системой трапецеидального вида. Для приведения к таковой надо сделать лишь следующую замену переменных:


 ,
, 




 ,
, 

 .
.
Относительно новых переменных система примет вид
который является трапецеидальным. Согласно сказанному в замечании, получаем, что система совместна, но неопределённа. Это можно было бы выяснить и с помощью теорем 1, 2 (по третьей таблице решения легко найти ранги матриц системы).
Ответ: Система совместна и неопределённа (бесчисленные множества решений).
Пример 40. Исследовать систему
методом элементарных преобразований.
Решение. Вычисления становятся более простыми, если за разрешающие элементы выбирать коэффициенты, равные единицам. Тогда разрешающие элементы 

 могут быть в произвольных местах таблицы, что сейчас и увидим. Заполняем исходную таблицу Гаусса и проводим итерацию, отмечая размещающие элементы на каждом этапе.
могут быть в произвольных местах таблицы, что сейчас и увидим. Заполняем исходную таблицу Гаусса и проводим итерацию, отмечая размещающие элементы на каждом этапе.
41

|
|
|
|
|
|
|
|
2 |
2 |
|
|
3 |
|
|
4 |
7 |
3 |
|
3 |
|
|
5 |
3 |
2 |
|
10 |
|
|
|
|
|
|
|
|
|
2 |
2 |
1 |
|
3 |
|
|
−2 |
|
0 |
|
−6 |
|
|
|
−1 |
0 |
|
4 |
|
|
|
|
|
|
|
|
|
2 |
2 |
1 |
|
3 |
|
|
0 |
−1 |
0 |
|
2 |
|
|
1 |
−1 |
0 |
|
4 |
|
|
|
|
|
|
|
|
На этом прямой |
ход метода |
Гаусса завершён. |
В результате получим следующую |
|||
систему уравнений:
Эта система не является ни треугольной, ни трапецеидальной (хотя из её вида одно решение очевидно). Для её преобразования к одному из указанных видов сначала поменяем местами второе и третье уравнения:
Теперь сделаем следующую замену переменных:





 ,
, 

 .
.
Относительно этих новых переменных система примет вид
который является треугольным. Таким образом, исходная система имеет единственное решение. Его можно найти следующим образом. Из последней системы обратным ходом метода Гаусса находится соответствующие 


 Совершив это действие, получим
Совершив это действие, получим
Возвратившись к замене переменных, находим исходные неизвестные:
Легко проверить, что это решение (2, 2, 3) удовлетворяет расширенной системе. Заметим ещё, что для самого нахождения этого решения (но не для доказательства его существования и единственности) перестановки уравнений и замены переменных проводить не нужно. Это решение сразу наблюдается при рассмотрении третьей таблицы «проведённых» преобразований.
42

Ответ: Система совместна и определённа, единственное решение имеет вид (2, 2, 3). Рекомендуем исследовать эту систему с помощью теорем 1 и 2. Примерами 37 − 40 продемонстрирован метод Гаусса исследования систем. При этом указаны и способы нахождения решений.
Перейдём к более простым примерам, возможным при тестировании. Если решение не нужно находить, то надо применять теоремы 1 и 2.
Пример 41. Исследовать систему
с двумя переменными (x, y и т.д. – обычное обозначение переменных в заданиях при тестировании с небольшим числом неизвестных).
Решение. Выпишем обе матрицы данной системы:
Миноры второго порядка есть миноры высшего порядка этих матриц. Для обеих матриц можно рассмотреть минор
который отличен от нуля. Тогда r (А) = 2 и r ( ) = 2. По теореме Кронекера − Капелли делаем вывод, что система совместна. Так как n = 2, то выполняется условие r = n. Следовательно, по теореме 2 решение единственно. Его легко найти каким-нибудь из методов исключения неизвестных (такие приёмы рассматривались в средней школе). В дальнейшем будут указаны и другие методы. Рекомендуем сразу применить к этой системе уже изложенный метод Гаусса.
) = 2. По теореме Кронекера − Капелли делаем вывод, что система совместна. Так как n = 2, то выполняется условие r = n. Следовательно, по теореме 2 решение единственно. Его легко найти каким-нибудь из методов исключения неизвестных (такие приёмы рассматривались в средней школе). В дальнейшем будут указаны и другие методы. Рекомендуем сразу применить к этой системе уже изложенный метод Гаусса.
Ответ: Система совместна и определённа, т.е. решение только одно.
Пример 42. Исследовать систему
Решение. Матрица А и расширенная матрица  этой системы таковы:
этой системы таковы:
Минорами высшего порядка этих матриц являются миноры второго порядка. Единственный минор второго порядка матрицы А есть минор, который равен нулю
следовательно, r(A) 2. Так как имеются её миноры первого порядка,
2. Так как имеются её миноры первого порядка,
отличные от нуля, то r (A) = 1. У матрицы  имеются миноры второго порядка,
имеются миноры второго порядка,
43

отличные от нуля (например, |
|
Так как |
r(A)  r (
r ( , то по теореме Кронекера − Капелли данная система противоречива. Ответ: Система противоречива (решений нет).
, то по теореме Кронекера − Капелли данная система противоречива. Ответ: Система противоречива (решений нет).
Пример 43. Исследовать систему
Решение. Очевидно, что минорами высшего порядка обеих матриц А и  являются миноры второго порядка. У них есть общий минор
являются миноры второго порядка. У них есть общий минор
отличный от нуля. Следовательно, по определению ранга имеем, что r(A) = 2 и r ( = 2; тогда по теореме 1 эта система совместна. Так как число неизвестных системы равно трём (n = 3), то r
= 2; тогда по теореме 1 эта система совместна. Так как число неизвестных системы равно трём (n = 3), то r  n. По теореме 2 система неопределённа.
n. По теореме 2 система неопределённа.
Ответ: Система совместна и неопределённа (имеет бесконечное множество решений).
Пример 44. Выяснить, при каком числе система линейных уравнений





несовместна.
Решение. Расширенная матрица системы имеет вид
Слева (до вертикальной черты) выписана матрица А системы. Вычислим минор второго (высшего) порядка расширенной матрицы, не содержащий элемент  :
:
По определению ранга r ( = 2. Тогда по теореме Кронекера − Капелли для несовместности системы ранг матрицы А должен быть равен единице. Это значит, что
= 2. Тогда по теореме Кронекера − Капелли для несовместности системы ранг матрицы А должен быть равен единице. Это значит, что
(определитель матрицы А) должен быть равен нулю. Из этого условия
находим  :
:
=2 





Отсюда следует, что 


Ответ: При 

 система не имеет решений.
система не имеет решений.
44

Пример 45. Выяснить, при каком  однородная система
однородная система





имеет ненулевые (нетривиальные) решения.
Решение. Однородная система совместных уравнений всегда совместна, так как она имеет нулевое (тривиальные) решение. В данном примере таким решением будет двумерный вектор (0,0). Для существования ненулевых решений необходимо и достаточно, чтобы выполнялось условие 


 (если
(если 


 , то нулевое решение
, то нулевое решение
будет единственным). Так как, |
|
|
|
то из уравнения |
|
|
|||||
|
|
|
|
|
|
получаем, что |
. |
|
|
|
|
Предлагаем читателю показать, как можно получать все частные решения данной системы.
Ответ: При 

 система имеет бесконечное множество ненулевых решений.
система имеет бесконечное множество ненулевых решений.
Пример 46. Требуется систему линейных уравнений
записать в матричном виде и указать матрицы этого вида.
Решение. Матричная запись системы линейных уравнений имеет вид
A  =B,
=B,
где А − матрица из коэффициентов при неизвестных; В – матрица − столбец из правых частей системы, а X – матрица − столбец из неизвестных. Ясно, что в этом примере
|
|
|
|
|
. |
|
Ответ: |
|
|
. |
|
|
|
Пример 47. Матрица B и обратная матрица |
|
к матрице А системы A =B |
||||
|
||||||
имеет вид |
|
= |
|
. Требуется найти решение системы. |
||
|
|
|||||
|
||||||
Решение. Матрица-столбец  системы A
системы A  = B с квадратной матрицей А находится по формуле
= B с квадратной матрицей А находится по формуле 



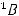 . Таким образом, надо найти матрицу
. Таким образом, надо найти матрицу 

 , т.е. произведение матриц
, т.е. произведение матриц 

 на матрицу В. Согласно данным задачи и правил из умножения матриц получим
на матрицу В. Согласно данным задачи и правил из умножения матриц получим
Итак, = |
; транспонируя эту матрицу, получим |
. Решение системы |
как вектор имеет вид 

45

Ответ:  =
=
Пример 48. Система линейных уравнений
решалась по формулам Крамера. Выяснить, какой из трёх указанных ниже ответов
1) |
|
|
|
2) |
|
|
|
3) |
|
|
|
|
является правильным.
Решение. Формулы Крамера для этой системы с двумя неизвестными x, y имеют
вид
где − определитель матрицы А = |
этой системы, |
отличный от нуля, |
− определитель, у которого j-й столбец определителя |
заменён столбцом из |
|
правых частей системы (другой столбец − такой же, как у  ). В этом примере, согласно сказанному и виду системы
). В этом примере, согласно сказанному и виду системы
|
|
, |
, |
|
|||
поэтому правильным ответом является только ответ 3). |
|
||
Ответ: 3), т.е. |
|
||
Замечание: Вычислим три определителя данного ответа:


 ,
, 



 ,
, 


 .
.
1. Легко проверить, что эти числа обращают равенства
Пример 49. Выписать матрицу линейного преобразования координат
и указать её размерность.
Решение. Этим преобразованием трёхмерного вектора
отображаются двумерные векторы |
Матрица А, составленная из |
коэффициентов при преобразуемых переменных |
, называется матрицей этого |
46

линейного преобразования. Очевидно, что А имеет вид |
|
, а её |
размерность − 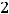

 , т.е. она имеет две строки и три столбца.
, т.е. она имеет две строки и три столбца.
Ответ: |
|
, размерность |
|
. |
|
|
Пример 50. Записать линейные преобразования переменных, заданное матрицей
Решение. Данное преобразование имеет вид
Очевидно, что оно преобразует векторы 




 из
из  в векторы
в векторы 




 из
из
 .
.
Ответ:
Пример 51. Найти собственные числа и соответствующие им собственные векторы линейного преобразования
Решение. Данное преобразование отражает вектор |
из |
в векторы |
из . Ему соответствует квадратичная матрица второго порядка |
|
|
. |
|
|
Преобразование можно записать в матричном виде |
|
. |
Матрица X размерности 

 , элементами которой являются координаты вектора
, элементами которой являются координаты вектора  , также будем называть векторами.
, также будем называть векторами.
Собственным вектором данного линейного преобразования с квадратной матрицей А (собственным вектором матрицы А) называется всякий ненулевой вектор X (X
 ), удовлетворяющий условию
), удовлетворяющий условию


 ,
,
где − некоторое число. При этом число  называется собственным значение линейного преобразования или собственным значением задающей это преобразование матрицы А. Если
называется собственным значение линейного преобразования или собственным значением задающей это преобразование матрицы А. Если  есть собственный вектор, принадлежащий собственному значению
есть собственный вектор, принадлежащий собственному значению
 , то при любом
, то при любом 

 вектор
вектор  также является собственным вектором.
также является собственным вектором.
Собственные значения  находятся как решения характеристического (векового)
находятся как решения характеристического (векового)
уравнения матриц А т.е. уравнения 




 . Для квадратной матрицы А
. Для квадратной матрицы А
второго порядка оно имеет вид
47

|
= 0. |
|
В данном примере это уравнение таково:
|
|
|
= |
0. |
|
|
||
|
|
|
|
|||||
|
|
|
|
|
|
|
||
|
|
|
|
|
уравнение |
|
|
|
Вычислив определитель, получаем алгебраическое |
|
|||||||
|
||||||||
второй степени относительно неизвестной  . Его корнями (характеристическими
. Его корнями (характеристическими
корнями матрицы А данного примера) |
являются числа |
|
|
|
|
|
Это и есть |
|||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
собственные числа линейного преобразования (матрицы А). |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
При каждом собственном числе собственный вектор X (с точностью до постоянной |
||||||||||||||||||||||||||||||
величины |
) находится (в случае |
|
|
|
) как решение системы |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В данном примере при |
|
1 система имеет вид |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Её решением является вектор ( |
|
|
, |
где − произвольное действительное |
||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
число. Таким образом, каждый вектор |
|
|
|
|
|
|
|
|
|
при |
|
|
|
является собственным |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
вектором, |
соответствующим собственному значению = |
|
|
1. При |
получим |
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
однородную систему уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
решением которой является вектор ( |
|
|
|
|
с произвольным действительным числом . |
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
Тогда |
каждый |
вектор |
|
, |
|
где |
, |
является собственным |
вектором |
|||||||||||||||||||||
рассмотренного линейного преобразования с собственным значением |
. |
|
|
|||||||||||||||||||||||||||
Ответ: Собственными числами |
линейного |
преобразования |
являются числа |
|||||||||||||||||||||||||||
= |
|
1, |
|
, им |
соответствуют |
|
собственные |
|
векторы |
|
|
|
, |
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
, где |
− произвольное действительное число, не равное нулю ( |
). |
|||||||||||||||||||||||||
Пример 52. Даны следующие четыре значения числа |
: |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
1) |
, |
2) |
|
|
, |
|
|
3) |
, |
|
4) |
. |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Выяснить, какие из этих чисел являются собственными значениями матрицы
.
48

Решение. Характеристическое уравнение этой матрицы имеет вид




|
|
Вычислив определитель, получим уравнение |
|
|
|
; тогда |
|
|
; тогда |
||||||
|
|
|
|||||||||||||
|
|
= |
. Следовательно, характеристическими корнями являются числа |
= |
|
1, |
|||||||||
|
|
|
|||||||||||||
|
. Они являются собственными значениями заданной матрицы. |
|
|
|
|
|
|||||||||
|
|
Ответ: = |
|
1, |
− собственные значения матрицы А. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||
Пример 53. Выписать матрицу А следующей квадратичной формы двух переменных 











 .
.
Решение: Квадратичная форма двух переменных имеет вид






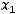




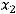



 .
.
Матрицей этой квадратичной формы называется квадратная матрица
,
причём предполагается, что эта матрица симметрична, т.е. 

 . Тогда исходную квадратичную формулу можно записать в виде
. Тогда исходную квадратичную формулу можно записать в виде








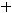

 .
.
Из данных примера имеем, что 

 ,
, 


 ,
, 


 (
(




 ). Следовательно, матрица квадратичной формы имеет вид
). Следовательно, матрица квадратичной формы имеет вид
Ответ: 

Пример 54. Выписать матрицу А квадратичной формы
трёх переменных 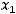

 .
.
Решение.Квадратичная форма трёх переменных имеет вид

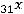









 ;
;
при этом предполагается, что её матрица
симметрична, т.е. 





 Тогда она приводится к виду
Тогда она приводится к виду
49



 .
.
Согласно вышеизложенному, для данной квадратичной формы
Следовательно, её матрица имеет вид
.
Ответ: |
. |
|||||
|
|
|
|
|
|
|
Пример 55. Записать квадратичную формулу, если её матрица имеет вид
Решение. По данным примера |
имеем |
|
Тогда |
||||
|
|||||||
искомая квадратичная форма (см. решение примера 53) такова: |
|||||||
|
( |
|
|
+6 |
. |
||
|
|
||||||
Ответ: ( |
|
+6 |
. |
|
|
|
|
|
|
|
|
|
|||
Пример 56. Записать квадратичную форму по её матрице
.
Решение. Данная матрица является симметричной матрицей третьего порядка, при этом 










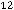








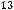






Тогда квадратичная форма есть форма трёх переменных и имеет вид (см. пример 54)










 +
+
Ответ: 












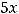


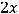




Пример 57. Найти ранги следующих квадратичных форм.
1) 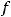





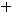





 ,
,
50

2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
|
|
|
|
|
|
, |
|
|
|||
|
|
|||||||||||
4) |
|
|
|
|
|
|
, |
|||||
|
|
|||||||||||
5) |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Рангом квадратичной формы называется ранг, задающий эту форму матрицы.
Матрицей первой формы f двух переменных является матрица (см. пример 53)
Единственный её минор высшего (второго) порядка совпадает с определителем этой матрицы. Очевидно, что 
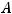







 . Тогда
. Тогда 


 и, следовательно, ранг квадратичной матрицы будет равен двум (будем писать
и, следовательно, ранг квадратичной матрицы будет равен двум (будем писать 


 ).
).
Матрицей второй заданной формы является матрица (см. пример 55).
Так как 










 , то
, то 


 ; тогда и
; тогда и 


 .
.
Третья заданная квадратичная форма определяется матрицей третьего порядка (см. пример 54)
определитель, которой |
|
|
|
|
|
|
|
|
|
. Тогда |
. |
|
|
|
|
|
Четвёртой квадратичной форме соответствует матрица (см. пример 56)
Так как 




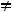
 (предоставляем проверить это читателю), то
(предоставляем проверить это читателю), то

 .
.
В пятом примере матрица формы такова:
(обращаем внимание, что эта форма с тремя переменными). Очевидно, что
. |
Так как |
имеется |
минор |
|
не |
равный |
нулю, то |
и, следовательно, |
. |
|
|
|
|
|
|
Ответы: 1) |
, 2) |
, 3) |
, 4) |
, 5) |
. |
|
|
|
|
|
51 |
|
|
|
|

Пример 58. Из квадратичных форм
1) 


2) |
, |
|
3) |
|
, |
|
||
4) |
, |
|
5) 



нужно выделить канонические (диагональные) формы.
Решение. Квадратичная форма n переменных называется канонической или диагональной, если она имеет вид
 .
.
Матрица А такой формы является диагональной, т.е.
.
(Элементы  главной диагонали есть коэффициенты при квадратах соответствующих переменных
главной диагонали есть коэффициенты при квадратах соответствующих переменных  , а остальные элементы равны нулю).
, а остальные элементы равны нулю).
Из перечисленных форм таковыми являются формы под номерами 2), 3) и 5). Отметим, что пятая форма есть квадратичная форма трёх переменных, а её матрица имеет вид
Ранг этой матрицы равен двум (укажите минор второго порядка, отличный от нуля), тогда и ранг этой формы равен двум.
Ответ: Квадратные формы под номерами 2), 3), 5) являются каноническими (диагональными).
Пример 59. Из канонических (диагональных) форм
1) |
, |
|||||
2) |
|
, |
||||
|
||||||
3) |
, |
|
|
|
|
|
4) |
|
|
|
|
, |
|
|
||||||
5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
нужно выделить формы нормального вида.
52

Решение. Канонический (диагональный) вид квадратичной формы называется нормальным видом, если коэффициенты  при переменных
при переменных  могут принимать своими значениями числа 1, − 1, 0.
могут принимать своими значениями числа 1, − 1, 0.
Согласно данному определению, диагональные формы 2), 3) и 4) являются формами нормального вида.
Ответ: Диагональные формы 2), 3) и 4) имеют нормальный вид.
Пример 60. Указать преобразование координат, с помощью которого каноническая форма
приведётся к нормальному виду относительно новых переменных. Выписать нормальный вид формы в новых переменных.
Решение. Очевидно, что таким преобразованием координат является линейное преобразование
(предлагаем читателю найти обратное преобразование и выписать матрицы этих преобразований). В новых переменных квадратичная форма примет нормальный вид





 .
.
Коэффициентами при новых переменных являются числа 1, 0, 1, 1. Ответ: Надо применить линейное преобразование
При этом форма приведётся к нормальному виду






 .
.
Пример 61. Найти ранги следующих квадратичных форм:
1) |
, |
|
||||
2) |
|
, |
|
|||
|
||||||
3) |
|
|
, |
|||
|
||||||
4) |
, |
|||||
5) |
|
|
. |
|||
|
||||||
Решение: Ранги этих форм можно найти путём нахождения рангов матриц, задающих эти формы (см. пример 57).
Так как все эти формы канонические (в частности, нормальные), то их ранги равны числу коэффициентов  , отличных от нуля (в случае нормального вида − числу единиц и (−1), без учёта нулей). Напомним, что
, отличных от нуля (в случае нормального вида − числу единиц и (−1), без учёта нулей). Напомним, что 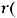


 , где n − число переменных
, где n − число переменных
53

квадратной формы. Из сказанного получаем следующие ответы: 1) |
, |
|||||
2) |
, 3) |
|
, 4) |
|
, 5) |
. |
В скобках указано число переменных формы. |
|
|
|
|||
|
Ответы: 1) |
, 2) |
, 3) |
, 4) |
, 5) |
. |
Пример 62. Выяснить, какие из квадратичных форм примера 61 являются невырожденными.
Решение. Квадратичная форма называется невырожденной, если 
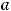






 , т.е.
, т.е. 


 . Согласно решению предыдущего примера невырожденным являются квадратичные формы 1), 2) и 3).
. Согласно решению предыдущего примера невырожденным являются квадратичные формы 1), 2) и 3).
Ответы: Невырожденными являются квадратичные формы 1), 2) и 3).
Пример 63. Привести квадратичную форму
к каноническому виду.
Решение. Всякая квадратичная форма некоторым линейным преобразованием переменных может быть приведена к каноническому виду, причём коэффициентами этого вида будут характеристические корни матрицы квадратичной формы, взятые с их кратностями. Так как матрица квадратичной формы симметрична, то корнями её характеристического уравнения будут действительные числа. В данном примере матрица А имеет вид
Её характеристическое уравнение таково:






или |
|
|
|
|
|
. Корни этого уравнения следующие: |
|
|



Таким образом, каноническим видом формы  является форма
является форма









 .
.
Ответ: 











 .
.
Пример 64. Выяснить знак квадратичной формы примера 63.
Решение. Квадратичная форма n переменных называется положительно определённой (отрицательно определённой), если
54

Для всех любых значений её переменных, не равных |
нулю одновременно. Форма |
|||
будет положительно определённой, если в каком-нибудь её каноническом виде |
||||
|
|
все коэффициенты |
|
положительны. Кроме того, |
равносильны следующие условия: |
|
|
||
1)квадратичная форма положительно определена;
2)собственные значения матрицы формы положительны.
Из решения предыдущего примера следует, что рассматриваемая форма положительно определена.
Ответ: 

 т.е. форма положительно определена.
т.е. форма положительно определена.
|
Пример 65. Выяснить, какая из квадратичных форм примера 59 является |
|||||
положительно определённой. |
|
|
|
|||
|
Решение. Такой формой является только первая форма двух переменных |
|
||||
|
|
|
|
|
, |
|
так |
как она |
уже имеет |
канонический |
вид, |
причём коэффициенты этого |
вида |
|
|
положительны (см. решение примера 64). Обратим внимание, |
что |
|||
третья форма двух переменных |
|
|
|
|||
не является положительно определённой, |
так как она обращается в нуль при |
и |
||||
любом |
(в её каноническом виде |
|
). Можно сказать, что эта форма |
|||
неотрицательна, так как |
для всех |
. Формы 2), 4) и 5) являются |
||||
знакопеременными. |
|
|
|
|
||
|
Ответ: Первая форма |
|
положительно определена. |
|
||
Пример 65. Исследовать квадратичные формы
1) 







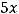












 ,
,
2) 


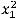









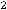


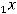



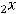

с помощью критерия Сильвестра.
Решение. Приведём два утверждения, называемые критериями Сильвестра.
1.Следующие условия равносильны:
1)квадратичная форма положительно определена;
2)все условные (главные) миноры её матрицы положительны.
2.Следующие условия равносильны:
1) квадратичная форма отрицательно определена;
55

2) все условные миноры нечётного порядка её матрицы отрицательны, а все угловые миноры чётного порядка положительны.
Напомним, что миноры матрицы − это возможные миноры первого и второго порядков, составленные из элементов этой матрицы.
Матрица первой квадратичной формы имеет вид
.
Её главные миноры таковы:
, |
, |
. |
(  − это обозначение определителя матрицы первого порядка (
− это обозначение определителя матрицы первого порядка (
 , а не обозначение абсолютной величины числа
, а не обозначение абсолютной величины числа  ). Так как все главы миноры положительны, то эта форма положительно определена.
). Так как все главы миноры положительны, то эта форма положительно определена.
У матрицы
второй квадратичной формы главные миноры таковы:
Таким образом, угловые миноры нечётного порядка (первого и третьего порядков) отрицательны, а угловой минор чётного (второго) порядка положителен. Тогда по второму утверждению Сильвестра эта форма отрицательно определена.
Ответ: Первая форма является положительно определённой, вторая − отрицательно определённой.
Пример 67. Найти все  , при которых форма
, при которых форма





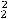















будет положительно определённой. Решение. Матрица этой формы имеет вид
.
Для положительной определённости, согласно критерию Сильвестра, все условные миноры должны быть положительными, т.е. должны выполняться следующие неравенства для определителей первого, второго и третьего порядков:

56
