решением которых являются все числа , удовлетворяющие неравенству .

Модуль 2. Аналитическая геометрия

Пример 1. Найти координаты вектора 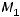, если его началом и концом являются точки (−1,3) и (2,5) плоскости.

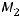
Решение. При любом расположении точек и на плоскости координаты X, Y вектора определяются равенствами

Решение. Воспользуемся решением предыдущего примера.

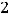
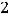
Так как найдутся из равенства

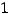
Тогда Ответ: Точка 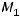имеет вид .

так:

.

При умножении вектора на число все его координаты умножаются на это число, а при сложении векторов соответствующие координаты складываются.

57

Ответ: .

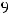
Пример 5. Выяснить, образуют ли базис в двумерном пространстве векторы

Решение. Базисом в пространстве (на плоскости) называются любые два неколлинеарных вектора на этой плоскости (ни один из них не может быть нулевым). Так как заданные векторы не являются нулевыми и коллинеарными (у коллинеарных векторов координаты пропорциональны), то они образуют базис. Можно рассуждать иначе. Базисные векторы линейно независимы. Необходимым и достаточным условием линейной независимости векторов является условие отличия от нуля определителя, составленного из координат этих векторов. В данном случае это условие выполняется:

Решение. Сразу отметим, что все векторы примера заданы в стандартном базисе пространства .

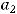В предыдущем примере установлено, что и образуют базис в . Разложить вектор по этому базису означает, что его надо представить в виде

В силу действий над векторами получим систему линейных алгебраических уравнений

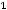
Известными методами легко установить, что эта система имеет единственное решение Таким образом, разложение имеет вид При этом говорят, что в базисе 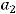вектор имеет своими координатами числа

58

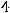
Ответ: Разложение по базису имеет вид

коллинеарны.

Решение. Ненулевые векторы 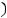и из коллинеарны тогда и только тогда, когда выполняются равенства

т.е. когда их координаты пропорциональны.

В данном случае условия коллинеарности имеют вид

.

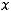
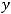
Согласно этим равенствам, получим, что Ответ: Координаты середины отрезка

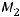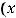
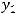
Пример 9. Точка является серединой отрезка . Найти координаты точки , если известна точка

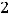
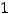
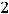
Решение. Воспользуемся равенствами, приведёнными при решении примера 8. По условию данного примера Тогда имеют место равенства

,

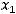
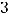
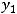
из которых находим, что Ответ: есть координаты точки .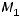

Пример 10. Найти скалярное произведение 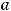и , если длины и угол между ними таковы: .

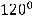Решение. Скалярные произведения ( векторов и определяется равенством

( .

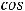59

Так как

Ответ:

.

Решение. Скалярное произведение двух векторов из трёхмерного пространства 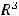равно сумме попарных произведений соответствующих координат этих векторов:

Так как вектор в координатной форме имеет вид

, − 4) будут коллинеарны.

Решение. Условием перпендикулярности (ортогональности) двух векторов является равенство

,

где 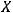− координаты . Так как заданный вектор в координатной форме имеет вид

.

Ответ:

Пример 14. Найти расстояние (A, B) между точками A(1,2) и B(4,6) из .

60

Пример 15. Вычислить угол между векторами

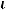
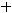
Решение. Из определения скалярного произведения векторов имеем равенство

Следовательно, =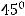

Ответ: =.

векторов выразим через координаты точек:

Аналогично предыдущему примеру найдём :

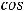
Следовательно, =.

Ответ: =.

Пример 17. Указать нормальный вектор прямой на плоскости, заданной её общим уравнением

61

Решение. Если прямая на плоскости задана её общим уравнением то её нормальный вектор (вектор, перпендикулярный этой прямой) имеет вид

В данном примере

которое преобразуется к виду

Ответ: есть общее уравнение искомой прямой.

Пример 19. Найти точки пересечения с осями координат прямой линии

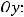
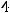
Решение. Положив в заданном уравнении найдётся точка пересечения прямой с осью координат Предположим в уравнении y = 0, найдём точку пересечения с осью Ox:

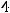
Ответ: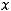

Пример 20. Требуется общее уравнение прямой 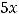привести к уравнению в отрезках, указав величины отрезков, отсекаемых этой прямой по осям координат.

Решение. Уравнение прямой на плоскости имеет вид

.

При этом числа a и b дают величины отрезков, которые прямая отсекает на координатных полуосях. Иначе говоря, прямая проходит через точки (a, 0) и (0, b). Данное общее уравнение легко преобразуется к виду

.

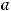
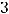
Это и есть уравнение заданной прямой в отрезках. При этом Ответ: Уравнение заданной прямой в отрезках имеет вид

есть величины отрезков отсекаемых прямой соответственно по оси Ox и оси Oy.

62

Решение. Уравнение данной прямой легко преобразовать к виду 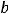т.е. к уравнению с угловым коэффициентом Действительно, преобразуется к виду а последнее − к виду Таким образом,

Ответ:

Пример 23. Написать общее уравнение прямой, проходящей через точку и имеющей угловой коэффициент

Решение. Воспользуемся уравнением

где есть точка, через которую проходит прямая, а − её угловой коэффициент. Тогда

63

коэффициент k = 2. Угловой коэффициент любой параллельной ей прямой также равен двум. Воспользовавшись уравнением примера 23, получим

которое приводится к виду

Ответ:

Пример 26. Составить уравнение прямой, проходящей через точку перпендикулярно прямой

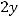
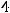
Решение. Уравнение заданной прямой как уравнение с угловым коэффициентом

Ответ: .

Подставляя координаты этих точек в это уравнение (очевидно, что условия выполняются), получим

Из последней пропорции следует, что ( Последнее уравнение легко преобразуется к общему уравнению прямой. Общее уравнение искомой прямой таково:

Из этой формулы и данных примера получим

64

Ответ: .

Пример 29. Найти угол между прямыми, уравнения которых таковы: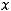

Решение. Одним из углов , образованных двумя прямыми, заданными их общими уравнениями, есть угол между их нормальными векторами (другой угол дополняется его до π). Тогда

Следовательно, один из этих углов, которые образуют эти прямые, равен

Ответ: =.

Пример 30. Вычислить угол между прямыми, уравнения с угловыми коэффициентами которых таково:

Решение. Будем искать острый угол между данными прямыми. Он отсчитывается против хода часовой стрелки от прямой с меньшим угловым коэффициентом до прямой с большим угловым коэффициентом. Если прямые неперпендикулярны, то тангенс этого угла определяется формулой

.

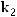
Так как то из этой формулы получим

.

Таким образом, .

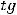
Ответ: .

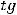
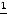Пример 31. Указать правильный вектор плоскости, заданной её общим уравнением

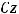
Решение. У плоскости, заданной её общим уравнением нормальным вектором является вектор В данному случае этим вектором будет вектор

65

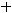
перпендикулярный данной плоскости и называемый нормальным вектором плоскости. Воспользовавшись этим уравнением, получим или

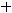
Последнее уравнение есть общее уравнение искомой плоскости. Ответ: Уравнение искомой плоскости имеет вид

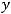
Пример 33. Написать общее уравнение плоскости, отсекающей по осям абсцисс, ординат и аппликат соответственно отрезки, величины которых таковы:

Решение. Уравнение плоскости в отрезках имеет вид

Согласно данным примера, получим

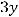
Отсюда легко прийти к уравнению которое и является общим уравнением плоскости.

Ответ: Общее уравнение искомой плоскости есть уравнение

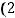
Пример 34. Составить канонические уравнения прямой в пространстве, проходящей через точку и параллельной вектору

Решение. Прямую в пространстве можно задать каноническими уравнениями

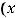
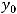
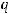
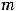
где некоторая точка этой прямой, а − ненулевой вектор, лежащий на данной прямой или параллельной ей и называемый направляющим вектором прямой. Тогда приходим к следующим каноническим уравнениям:

.

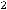
Ответ: Канонические уравнения искомой прямой таковы:

.

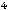
Пример 35. Составить параметрические уравнения пространственной прямой, проходящей через точки

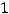
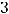
66

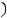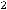
Решение. Уравнение прямой, проходящей через две данные точки и , имеет вид

Отсюда, из условий примера, получим следующие канонические уравнения:

.

Параметрические уравнения получим, если каждое из последних отношений приравняем к параметру t:

Последние уравнения можно записать в виде

Ответ: Параметрические уравнения искомой прямой имеют вид

Пример 36. Указать, при каком числе l прямая параллельна

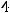
плоскости Решение. Прямая в пространстве будет параллельна плоскости, если её

67

правая часть которой есть определитель третьего порядка. При этом первая строка этого определителя состоит из координатных ортов 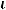вторая строка состоит из координат вектора , а третья − из координат вектора 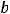. В данном случае имеем

Вычислим последний определитель по элементам первой строки. Коэффициентами при соответственно будут алгебраические дополнения:

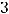
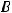
Пример 38. Найти площадь треугольника с вершинами Решение. Площадь треугольника ABC равна половине площади параллелограмма,

построенного на векторах

,

где есть угол между этими векторами. С другой стороны, длина вектора

определяется равенством

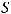
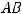
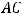
Таким образом, Из этого равенства и будем исходить. Так как

то

.

Тогда

Ответ:

68

Решение. Сначала найдём векторные произведения векторов т.е. вектор (см. пример 37), а потом скалярное произведение этого вектора и вектора Так как

Ответ: ( )=10.

Пример 40. Составить уравнение окружности с центром в точке и радиусом

Решение. Уравнение окружности с центром в точке радиуса имеет вид

Из условия примера получим

Ответ: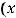

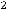
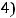
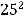
Пример 41. Указать центра С и радиус r окружности, уравнение которой имеет вид

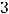
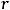
Решение. Очевидно, что (см. предыдущий пример). Таким образом, центр С имеет координаты (− 5, 3), а радиус окружности

Ответ: С= (− 5, 3);

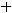
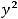
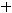
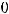
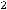
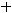
Пример 42. Исследовать, какую кривую задаёт уравнение Решение. Данное уравнение имеет вид т.е. имеет

равные коэффициенты при квадратах переменных, а член, содержащий произведения отсутствует. Если такое уравнение задаёт какую-нибудь невырожденную кривую на плоскости, то ей будет окружность. Для выяснения ситуации данное уравнение

преобразуем, сгруппировав члены с переменными и выделив полные квадраты:

69

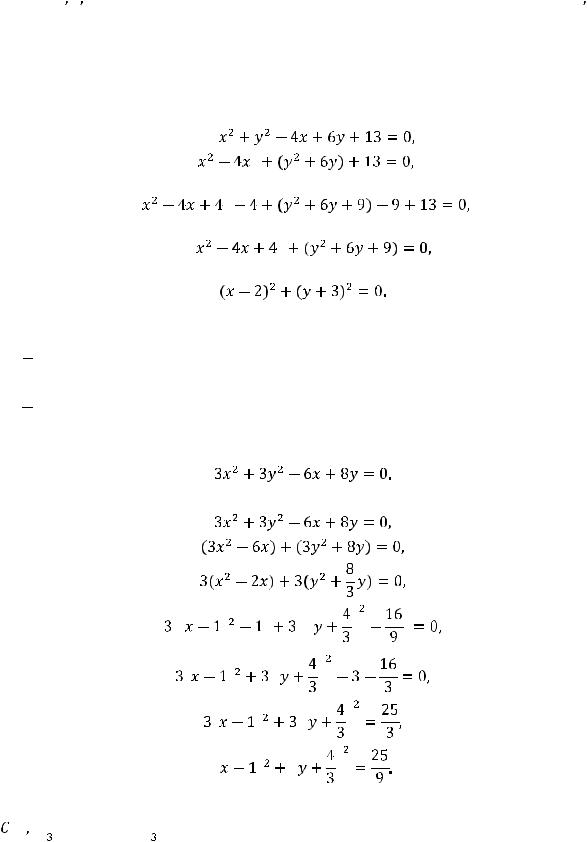
В последнем уравнении левая часть не отрицательна при любых действительных числах 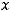правая часть отрицательна. Данному уравнению ни одна пара (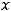 действительных чисел не удовлетворяет. Уравнение никакой линии не задаёт.

Ответ: Уравнение примера никакой действительной кривой не задаёт.

Пример 43. Будем учитывать сказанное при решении предыдущего примера. Снова проведём такие же преобразования с данным уравнением:

Ясно, что последнему уравнению удовлетворяют координаты только одной точки

(2, 3).

Ответ: Уравнение задаёт вырожденную кривую, т.е. одну точку с координатами

(2, 3).

Пример 44. Выяснить, какую линию задаёт уравнение

Решение. Проводим преобразования данного уравнения:

Из последнего уравнения видно, что линией является окружность с центром в точке радиуса

70

Пример 45. Указать каноническое уравнение эллипса с полуосями

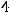
Решение. Если 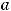– полуоси эллипса, то его каноническое уравнение имеет вид

В данном случае этим уравнением будет

Ответ: .

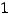Пример 46. Составить уравнение эллипса с центром в точке 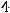и полуосями

Решение. Уравнение эллипса с центром в точке и полуосями имеет вид

По условию данного примера получим уравнение

Ответ:

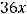
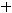
Пример 47. Определитьгеометрическийтипкривой Решение. Сгруппируем данные и выделим полные квадраты:

Разделив последнее равенство на 36, получим уравнение

Такое уравнение (см. пример 46) задаёт эллипс с центром в точке C (2, −1) и полуосями a = 2, b = 3.

Ответ: Уравнение задаёт эллипс с центром в точке C (2, −1) и полуосями a = 2, b = 3.

Пример 48. Найти эксцентриситет эллипса

71

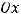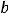Решение. Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси. Если фокусы эллипса лежат на оси и длина большой оси есть ( – длина малой оси, ), то эксцентриситет эллипса есть число

При этом В данном примере Так как

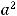
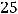
Ответ:

Пример 49. Указать вершины 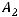и фокусы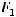 гиперболы

Решение. Если каноническое уравнение гиперболы имеет вид

Решение. Асимптотами гиперболы с каноническим уравнением

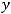
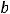
Являются прямые линии Так как в данном примере то асимптотами являются прямые

Ответ: Асимптотами гиперболы являются прямые

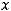
Пример 51. Найти эксцентриситет 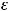гиперболы

Решение. Эксцентриситетом гиперболы вида

72

называется расстояние между фокусами к длине 2a действительной оси:

Ответ:

Пример 52. Указать центр С и длины 2a и 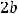действительной и мнимой осей гиперболы.

Решение. Данное уравнение имеет вид

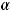
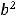
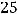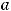
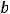
Это будет гипербола с центром в точке и осями, параллельными координатным осям. При этом a − длина действительной полуоси, b − длина мнимой полуоси. В данном случае, центром является точка Так как то Следовательно, 2a = 8 и 2b = 10.

Ответ:

Пример 53. Выяснить геометрический тип кривой, заданной уравнением

Решение. Сгруппируем члены с переменными и выделим полные квадраты:

Разделив последнее равенство на 16, получим уравнение

Пример 54. Определить центр С, вершины 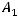и длины полуосей гиперболы

Решение. Так как уравнение имеет вид

гиперболы находятся на действительной оси. Вторая координата вершины есть число

Ответ:

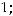
Пример 55. Найти директрису и фокус F параболы, заданной каноническим уравнением .

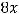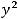
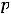
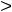
Решение. Если каноническое уравнение параболы имеет вид 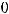то точка F ( является фокусом, а вертикальная прямая директрисой этой параболы. Парабола имеет вершину в начале координат и симметрична относительно оси . В данном случае , тогда Фокусом является точка F(2,0). Директрисой будет вертикальная прямая

Ответ: Фокус параболы есть точка F(2,0), директриса − вертикальная прямая x = 2.

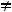
Пример 56. Найти вершину параболы, заданной уравнением Решение. При уравнение

задаём параболу, ось которой параллельна оси ординат Oy. Если такое уравнение преобразовать к виду

то сразу определяется вершина параболы, которой является точка Преобразуем данное уравнение, выделив в его части полный квадрат:

74