
- •Кафедра математики и математических методов в экономике
- •ЛИНЕЙНАЯ АЛГЕБРА
- •Предисловие
- •Тестовые задания для самостоятельной работы
- •Тестовые задания с решениями
- •Модуль 1. Матричная алгебра
- •Модуль 2. Аналитическая геометрия
- •Модуль 3. Элементы комплексного анализа
- •Библиографический список
- •Содержание
- •ЛИНЕЙНАЯ АЛГЕБРА

Задание 28. Линейное пространство образует множество… Варианты ответов: 1) натуральных чисел; 2) положительных чисел; 3)
положительных целых чисел; 4) действительных (вещественных) чисел.
Задание 29. Произведением комплексных чисел |
|
|
|
и |
|
|
|
, |
||||||||||||||
|
||||||||||||||||||||||
заданных в алгебраической форме, является число… |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Варианты ответов: 1) 5 |
|
i; 2) 12 |
|
5i; 3) 6 |
|
6i; 4) 6 |
|
i. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Задание 30. Произведением комплексных чисел |
|
|
|
|
|
и |
|
, заданных в |
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
показательной форме, является число… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Варианты ответов: 1) 7 |
|
|
|
; 3) |
|
|
; 4) |
|
|
|
. |
|
|
|
|
|
|
|||||
|
|
; 2) 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Тестовые задания с решениями
Задание 1. Если транспонированная матрица 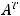 матрицы
матрицы 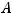 имеет вид
имеет вид
то элемент |
матрицы равен … |
|||
Варианты ответов: 1) 3; 2) 4; 3) |
|
1; 4) 2. |
||
|
||||
Решение. Строки матрицы |
являются соответствующими по номеру столбцами её |
|||
транспонированной матрицы |
. Следовательно, матрица имеет вид |
|||
тогда 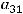


 . Можно рассуждать ещё так. Элемент
. Можно рассуждать ещё так. Элемент 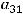 матрицы
матрицы 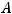 будет элементом
будет элементом 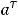 транспонированной матрицы
транспонированной матрицы 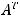 , из вида которой следует, что
, из вида которой следует, что 


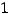

Задание 2. Если матрица 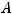 имеет размерность
имеет размерность 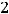
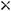
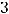 , а В
, а В
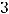
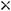
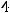 , то их произведение
, то их произведение 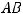 имеет размерность…
имеет размерность…
Варианты ответов: 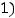
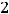
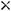

Решение. Размерность матрицы 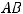 при заданных размерностях А и В выражается символической схемой
при заданных размерностях А и В выражается символической схемой
Так как |
то |
= |
Итак, размерность АВ есть |
, т.е. правильным ответом является ответ 2). |
|
||
9

Задание 3. Произведение матрицы |
на матрицу |
есть матрица …
Варианты ответов: 1)
Решение: Так как размерность матрицы 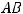 должна быть
должна быть 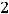
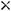
 (см. предыдущий пример), то варианты ответов 1) и 2) отпадают. Тогда возможны ответы 3) и 4), так как обе эти матрицы имеют размерность
(см. предыдущий пример), то варианты ответов 1) и 2) отпадают. Тогда возможны ответы 3) и 4), так как обе эти матрицы имеют размерность 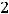
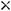
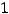
 Очевидно, что 4) отпадает ввиду того, что эта матрица нулевая (по виду А и В этого быть не может). Правильным ответом является ответ 3). Это легко и проверить по правилу умножения матриц.
Очевидно, что 4) отпадает ввиду того, что эта матрица нулевая (по виду А и В этого быть не может). Правильным ответом является ответ 3). Это легко и проверить по правилу умножения матриц.
Задание 4. Элемент |
произведения матрицы |
|
|
на матрицу |
|||||||
равен… |
|
|
|
|
|
|
|
|
|
|
|
Варианты ответов: 1) 0; 2) |
|
100; |
3) 5; 4) 18. |
|
|
|
|
||||
|
|
|
|
|
|||||||
Решение. |
Согласно |
правилу |
умножения матриц |
элемент |
матрицы AB |
||||||
получается путём умножения элементов второй строки матрицы A на соответствующие |
|||||||||||
элементы правого столбца матрицы B и сложения полученных произведений. Тогда |
|||||||||||
|
|
Отметим следующее: зная правило умножения матриц, сразу |
|||||||||
можно было догадаться, что ответы 1), 2) не годятся. |
|
|
|
|
|||||||
Задание 5. Если определитель |
|
|
матрицы равен |
|
|
|
, то элементом |
||||
этой матрицы является… |
|
|
|
|
|
|
|
||||
Варианты ответов: 1) 0; 2) 20; |
3) |
|
50; 4) 30. |
|
|
|
|
||||
|
|
|
|
|
|||||||
Решение. |
Определитель |
квадратной матрицы второго порядка вычисляется |
|||||||||
по формуле |
|
|
|
|
|
|
|
|
|
|
|

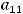
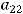

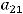
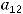 ,
,
т.е. он равен произведению элементов главной диагонали минус произведение элементов второй (побочной) диагонали. Для получения ответа проще всего и применить это правило. Тогда 
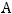

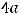
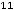

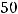
 Так как по условию дано, что
Так как по условию дано, что 
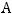


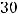 , то приходим к равенству
, то приходим к равенству 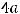
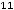

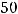

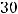 , т.е.
, т.е. 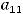

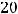
 Ответом является ответ 4). Отметим следующее. Достаточно быстро получим ответ, если вместо
Ответом является ответ 4). Отметим следующее. Достаточно быстро получим ответ, если вместо 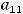 будем брать указанные в вариантах ответов числа (
будем брать указанные в вариантах ответов числа (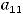

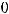
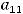

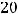
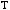

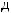

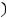 и вычислять определитель по произведённому правилу. Очевидно, что подходит вариант 2), т.е.
и вычислять определитель по произведённому правилу. Очевидно, что подходит вариант 2), т.е.


 .
.
10

Задание 5. Разложение определителя
по третьей строке имеет вид…
Варианты ответов:
1) 

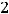

2) 

3) 

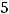

4) 

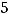

Решение. Правило Лапласа (разложение определителя по какой-нибудь строке или какому-нибудь столбцу) в данном задании будет иметь вид
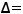
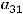
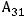
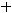
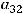
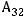
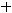
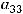
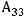 ,
,
т.к. разложение ведётся по третьей строке. Тогда в ответах надо искать случаи, где находятся элементы 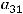

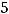
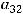


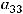

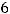
 Это случаи 3) и 4), а случаи 1) и 2) не годны. Так как дополнения вычисляются по формуле
Это случаи 3) и 4), а случаи 1) и 2) не годны. Так как дополнения вычисляются по формуле 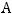

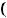

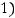

 , то алгебраическое дополнение
, то алгебраическое дополнение 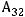 элемента
элемента 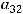

 таково:
таково:
Это означает, что правильным ответом является ответ 3).
Задание 7. Для матрицы А существует обратная, если А имеет вид…
Варианты ответов: 1) |
2) |
|
|
|
|
3) |
|
|
|
4) |
|
|
|
|
|
|
|||
Решение. |
Обратная |
матрица |
|
к |
матрице |
|
|
существует, если |
|||||||||||
|
|||||||||||||||||||
Очевидно, что только |
определитель |
матрицы |
|
|
|
|
|
не равен нулю |
|||||||||||
( |
|
|
Таким образом, только матрица 4) имеет обратную. |
||||||||||||||||
|
|
||||||||||||||||||
Задание 8. Обратная матрица |
|
|
к матрице |
|
|
имеет вид … |
|||||||||||||
|
|||||||||||||||||||
Варианты ответов: 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. |
|
Должны выполняться равенства |
|
|
|
|
|
|
|
|
где |
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||
есть единичная матрица второго порядка.
11

Очевидно, что эти равенства выполняются только для матрицы 3). Например, 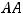



Опишем другой путь. Обратная матрица 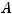

 имеет вид
имеет вид
где |
есть определитель матрицы А, а |
– алгебраические дополнения |
||||||||||
элементов |
матрицы А. Вычислим определитель матрицы А: |
|
|
|||||||||
|
||||||||||||
|
Из вида А имеем следующее: |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда по указанному виду 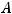

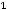 получаем, что
получаем, что
т.е. ответ 3).
Задание 9. Решение системы линейных уравнений
методом Крамера указано правильно в ответе …
Варианты ответов:
Решение. Если система линейных уравнений с двумя неизвестными 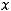
 имеет вид
имеет вид
то при |
её единственное решение можно получить по формулам |
Крамера
 .
.
Из этих формул, очевидно, что решение даётся ответом 2).
12
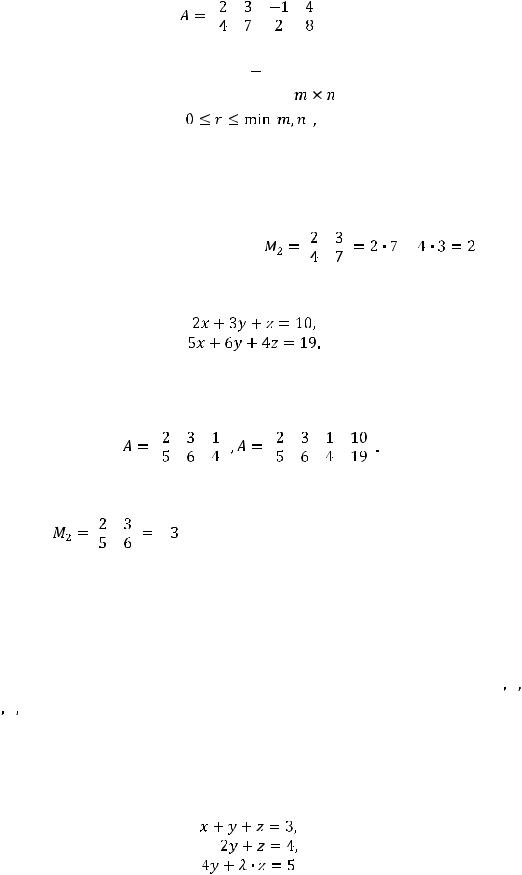
Задание 10. Ранг r матрицы |
|
равен… |
|
Варианты ответов: 1) 2; 2) 0; 3) 3; 4) 2. |
|
Решение. Ранг r любой матрицы размерности |
удовлетворяет неравенствам |
при этом только у нулевой матрицы ранг равен нулю. Следовательно, ответы 2) и 4) отпадают. Ранг равен наивысшему порядку отличных от нуля миноров, порождённых этой матрицей. В данном примере миноров третьего и высшего порядков нет, тогда отпадает и ответ 3). Остаётся ответ 1), т.е. 

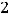
 Это действительно так: первый
Это действительно так: первый
взятый минор высшего (второго) порядка |
|
не равен |
|
нулю.
Задание 11. Система линейных уравнений
Варианты ответов: 1) не имеет решений; 2) имеет два решения; 3) имеет единственное решение; 4) имеет бесконечное множество решений.
Решение. Матрица 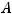 системы и расширенная матрица
системы и расширенная матрица 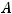 этой системы таковы:
этой системы таковы:
Очевидно, что ранги этих матриц совпадают и равным двум (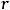
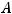

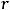
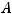

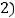 , т.к. у них имеются миноры высшего (второго) порядка, отличные от нуля. Например, у обеих
, т.к. у них имеются миноры высшего (второго) порядка, отличные от нуля. Например, у обеих
матриц минор |
|
не равен нулю. По критерию совместности (теореме |
|
Кронекера-Капелли) такая система совместна, т.е. имеет решения. Так как общий ранг 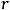

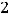 , а число неизвестных
, а число неизвестных 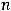

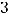 , то выполняется условие
, то выполняется условие 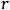
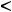
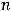 . Тогда из критерия определённости следует, что система имеет бесконечное множество решений. Таким образом, справедлив ответ 4). К нему можно прийти иначе, с помощью знаний из аналитической геометрии. Каждое уравнение системы задаёт в трёхмерном пространстве некоторую плоскость. Координаты нормальных векторов,
. Тогда из критерия определённости следует, что система имеет бесконечное множество решений. Таким образом, справедлив ответ 4). К нему можно прийти иначе, с помощью знаний из аналитической геометрии. Каждое уравнение системы задаёт в трёхмерном пространстве некоторую плоскость. Координаты нормальных векторов, 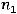


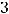
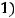 и
и 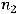


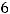
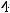 этих плоскостей не пропорциональны. Следовательно, эти плоскости непараллельны и не совпадают. Тогда они пересекаются по некоторой прямой в пространстве. Координаты точек этой прямой и являются решением системы, множество решений бесконечно.
этих плоскостей не пропорциональны. Следовательно, эти плоскости непараллельны и не совпадают. Тогда они пересекаются по некоторой прямой в пространстве. Координаты точек этой прямой и являются решением системы, множество решений бесконечно.
Задание 12. Система линейных уравнений
несовместна, если 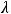 равно …
равно …
13
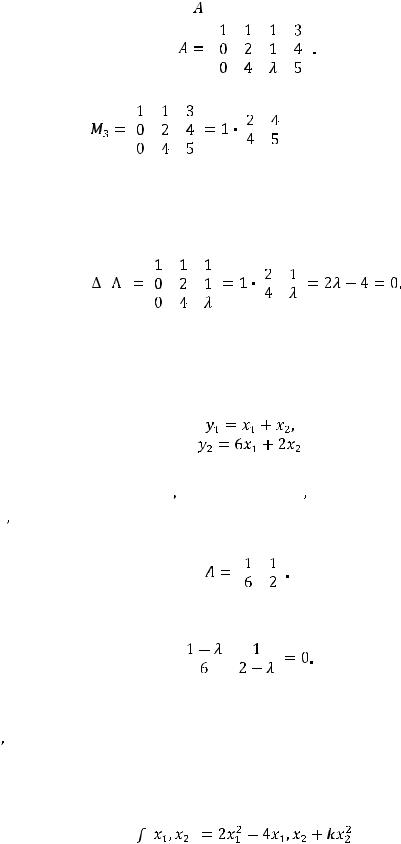
Варианты ответов: 1) 2; 2) 0; 3) |
|
1; 4) 1. |
|
||
Решение. Расширенная матрица |
этой системы имеет вид |
|
Вычисляем её минор высшего (третьего) порядка, не содержащий элемент 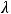 :
:

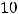

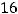


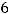 .
.
Так как он отличен от нуля, то ранг этой матрицы равен трём. (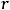
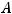

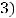 . Для несовместимости системы по теореме Кронекера − Капелли ранг матрицы
. Для несовместимости системы по теореме Кронекера − Капелли ранг матрицы 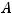 системы должен быть равен трём (
системы должен быть равен трём (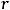
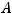

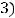 . Это значит, что определитель матрицы системы должен быть равен нулю:
. Это значит, что определитель матрицы системы должен быть равен нулю:
Отсюда следует, что 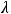

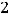
 Правильным ответом является ответ 1).
Правильным ответом является ответ 1).
Задание 13. Собственные значения 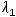 и
и 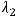 линейного преобразования
линейного преобразования
указаны правильно в ответе …
Варианты ответов: 1) 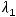

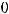
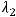

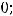 2)
2) 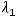

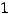
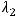

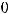 ; 3)
; 3) 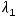


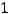 ,
, 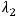

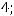 4)
4) 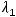

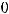
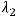

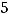

Решение. Матрица 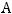 этого преобразования такова:
этого преобразования такова:
Характеристическое уравнение этой матрицы (данного линейного преобразования) имеет вид
Вычислив этот определитель второго порядка, получим уравнение второй степени относительно  , а именно уравнение
, а именно уравнение 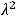

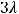

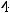

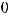
 Его действительные корни
Его действительные корни 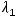


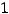
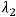

 и будут собственными значениями заданного линейного
и будут собственными значениями заданного линейного
преобразования. Правильным ответом является только ответ 3).
Задание 14. Квадратичная форма
будет положительной определённой при k …
Варианты ответов: 1) 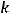
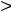
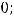 2)
2) 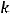

 ; 3)
; 3) 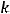

 ; 4)
; 4) 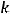


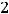 .
.
14

Решение. Матрица 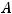 квадратичной формы имеет вид
квадратичной формы имеет вид 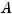

 . По критерию
. По критерию
Сильвестра данная квадратичная форма  будет положительно определённой только при условии положительности всех её главных (угловых) миноров, которыми являются
будет положительно определённой только при условии положительности всех её главных (угловых) миноров, которыми являются
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Тогда должно выполняться неравенство |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
Следовательно, правильным ответом является ответ 2). |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
Задание |
15. Векторы |
|
|
|
|
|
|
|
|
|
таковы: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Тогда линейная комбинация |
|
|
|
|
|
|
в этом базисе имеет вид … |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
Варианты ответов: |
1) |
|
|
2) |
; 3) |
|
|
|
; 4) |
|
|
|
|
|
. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
Решение. |
При умножении вектора на число каждая его координата умножается на |
|||||||||||||||||||||||||||||||||||||||||||||
это число. |
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При вычитании |
векторов |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
соответствующие координаты вычитаются. |
Поэтому |
|
|
|
|
в координатной форме |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а его разложение |
по стандартному базису |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
таково: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, т.е. ответом является ответ 1). |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
Задание 16. Длина |
|
|
вектора |
|
|
|
|
равна… |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
Варианты ответов: 1) 0; |
2) – 15; 3) 15; |
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
Решение. |
Если X, Y, Z – координаты вектора |
, то его длина вычисляется по |
||||||||||||||||||||||||||||||||||||||||||||
формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Так как |
|
|
|
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ответом является ответ 3). Отметим следующее: ответы 1) и 2) сразу отпадают, т.к.
только у нулевого вектора длина равна нулю ( |
|
и длина не может быть |
|
|
|||
отрицательным числом. |
|
|
|
Задание 17. Векторы |
и |
|
перпендикулярны, если |
равно … |
|
|
|
Варианты ответов: 1) 0; |
2) 1; 3) 5; |
4) –5. |
Решение. Векторы и |
перпендикулярны (ортогональны) тогда и только тогда, |
|
когда их скалярное произведение ( , |
) равно нулю (( , ) ). Так как скалярное |
|
произведение равно сумме попарных произведений соответствующих координат этих
векторов, то приходим к равенству |
или |
Следовательно, |
||
|
|
. Правильным ответом является ответ 4). |
|
|
|
|
|
|
|
15

Задание 18. Общее уравнение прямой, происходит через точку |
|
|||||||||||||||
перпендикулярно вектору |
|
|
имеет вид … |
|
|
|
|
|||||||||
Варианты ответов: 1) |
|
|
|
2) |
3) |
; |
||||||||||
|
||||||||||||||||
4) |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
Для получения ответа можно воспользоваться уравнением |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
|
координаты точки |
, а |
есть нормальный вектор этой прямой. |
||||||||||||
|
||||||||||||||||
Тогда имеем |
|
|
|
|
|
|
|
|
или |
|
|
т.е. имеем прямую 1). |
||||
|
|
|
|
|
|
|
|
|
||||||||
Можно рассуждать иначе. Так как в общем уравнении прямой |
числа |
|||||||||||||||
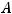
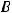 являются координатами нормального вектора
являются координатами нормального вектора 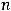 , то варианты ответов 3) и 4) негодны. Ответ может быть либо 1), либо 2). Для выбора окончательного ответа надо
, то варианты ответов 3) и 4) негодны. Ответ может быть либо 1), либо 2). Для выбора окончательного ответа надо
подставлять в это уравнение координаты точки |
(1, 2). Тождество получим только в |
||||||||
случае 1). |
|
|
|
|
|
|
|
|
|
Задание 19. Прямые |
|
|
|
и |
перпендикулярны, если угловой |
||||
|
|
|
|||||||
коэффициент k равен … |
|
|
|
|
|
|
|
|
|
Варианты ответов: 1) |
|
; 2) 2; 3) |
|
|
|
; 4) 1. |
|
||
|
|
|
|
||||||
Решение. Условием перпендикулярности прямых является равенство 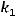
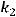
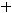


 или
или 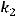


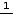 , где
, где 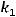
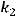
 угловые коэффициенты этих прямых. По условию задачи
угловые коэффициенты этих прямых. По условию задачи
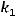

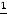 ,
, 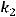

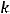 . Тогда
. Тогда 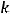




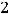 т.е. случай 1).
т.е. случай 1).
Задание 20. |
Уравнение прямой, проходящей через точку |
( −4, 8) параллельно |
|||||||
прямой |
|
имеет вид … |
|
|
|
|
|
||
|
|
|
|
|
|
||||
Варианты ответов: 1) |
|
|
2) |
|
; 3) |
|
|
||
|
|
|
|
||||||
4) 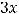
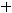
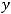

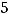

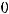

Решение. Очевидно, что заданная прямая имеет угловой коэффициент 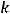


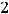
 Любая параллельная ей прямая имеет тот же угловой коэффициент. Тогда воспользуемся уравнением
Любая параллельная ей прямая имеет тот же угловой коэффициент. Тогда воспользуемся уравнением
и тем, что точка 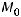 задана. Получим
задана. Получим 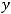




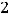


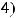 или
или 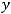


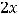
 Следовательно, такой прямой является прямая 1). Можно рассуждать иначе. Так как ответы даны, то среди этих прямых надо искать уравнения с угловым коэффициентом
Следовательно, такой прямой является прямая 1). Можно рассуждать иначе. Так как ответы даны, то среди этих прямых надо искать уравнения с угловым коэффициентом 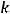


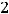 . Или являются прямые 1) и 2). Теперь надо учесть, что искомая прямая проходит через точку
. Или являются прямые 1) и 2). Теперь надо учесть, что искомая прямая проходит через точку 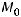

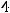

 Подставляя координаты этой точки в уравнения 1) и 2), убедимся, что такой прямой является прямая 1), т.е.
Подставляя координаты этой точки в уравнения 1) и 2), убедимся, что такой прямой является прямая 1), т.е. 


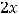 ,
, 





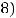 .
.
16

Задание 21. Через начало координат проходят прямые …
Варианты ответов: 1) 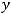

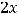
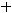
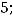 2)
2) 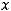

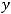

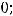 3)
3) 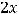
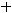
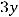

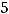

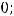 4)
4) 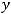

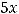

Решение. Очевидно, что такими прямыми являются 2) и 4). Это проверяется путём подстановки координат точки 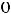

 в эти уравнения.
в эти уравнения.
Задание 22. Точка пересечения прямой 


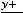
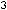



 и плоскости
и плоскости 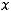
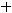
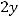
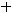
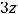
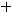
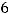

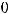 имеет координаты …
имеет координаты …
Варианты ответов: 1) (1; 
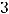 ; 5); 2) (1; 1; 4); 3) (
; 5); 2) (1; 1; 4); 3) (
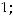


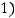
 4) (1, 2, 3).
4) (1, 2, 3).
Решение. Так как в ответах даны координаты предполагаемой точки, то проще всего установить нужную проверкой, т.е. подставлением координат этих точек в оба уравнения. Очевидно, что такой точкой является только точка 3). Если бы ответ был неизвестен, то следует действовать так. Получим параметрические уравнения заданной пространственной прямой:
Для нахождения координат точки пересечения надо решать систему уравнений
Решая её, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
, т.е. |
|||||||||||
|
||||||||||||||||||||||||||
пара метр |
|
|
Подставляем найденное значение в параметрические уравнения |
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
прямой: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эти |
числа |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
являются координатами точки пересечения. |
|
|
|
|
|
|
|
|||||||||||||||||||
Задание 23. Если уравнение окружности имеет вид |
|
|
|
|
|
|
то её |
|||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
центром С и радиусом r являются … |
|
|
|
|
|
|
|
|||||||||||||||||||
Варианты ответов: 1) С (5, 3), r = 4; 2) С(5, |
|
3), r = 4; |
3) С ( |
|
5, 3), r = 16; |
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||||||
4) С (5, |
|
3), |
r = 16. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
Решение. Уравнение окружности с центром в точке С ( |
|
|
|
радиуса r имеет вид |
||||||||||||||||||||||
В данном примере 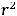

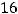 , т.е. r=4. Поэтому возможны ответы 1) и 2). Очевидно, что правильным ответом является 2).
, т.е. r=4. Поэтому возможны ответы 1) и 2). Очевидно, что правильным ответом является 2).
Задание 24. Алгебраическое уравнение второй степени задаёт на плоскости …
Варианты ответов: 1) параболу; 2) гиперболу; 3) эллипс; 4) окружность.
17
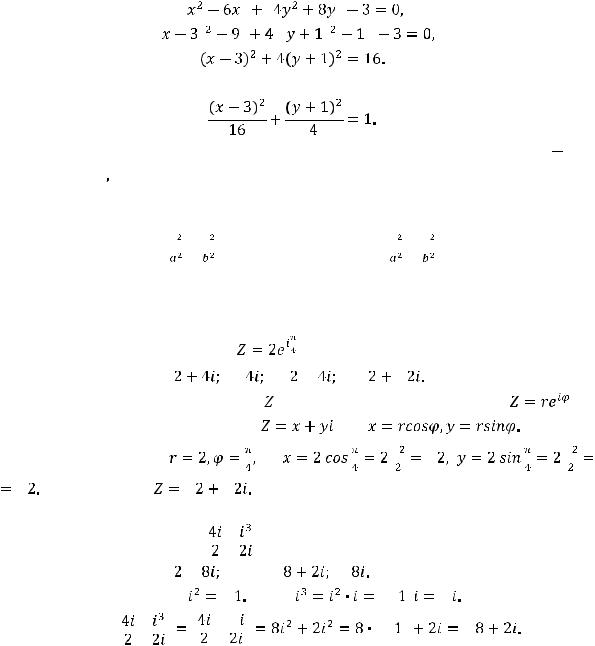
Решение. В уравнении присутствуют члены с  и
и 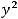 , такое уравнение не может задавать параболу. Коэффициент A при
, такое уравнение не может задавать параболу. Коэффициент A при 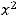 равен единице (A=1), а коэффициент B при
равен единице (A=1), а коэффициент B при 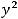 равен четырём (B = 4). Так как A
равен четырём (B = 4). Так как A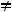 B, то это не окружность. Так как коэффициенты A и B одного знака, то эта кривая не является гиперболой. Следовательно, кривой является эллипс (правильным ответом является ответ 3)). Этот ответ можно получить следующим образом. Сгруппируем члены с соответствующими переменными и выделим полные квадраты:
B, то это не окружность. Так как коэффициенты A и B одного знака, то эта кривая не является гиперболой. Следовательно, кривой является эллипс (правильным ответом является ответ 3)). Этот ответ можно получить следующим образом. Сгруппируем члены с соответствующими переменными и выделим полные квадраты:
Разделив последнее равенство на 16, получим уравнение
Это уравнение определяет на плоскости эллипс с центром в точке С (3, 1) и полуосями 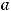

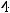
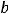

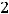

Задание 25. Каноническое уравнение параболы есть уравнение …
Варианты ответов: 1)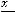
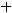
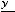

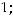 2)
2) 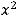
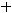
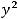

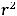
 3)
3) 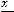

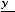

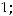 4)
4) 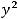

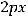

Решение. Таким уравнением является уравнение 4). Первое задаёт эллипс, второе − окружность, третье − гиперболу.
Задание 26. Комплексное число |
|
|
|
|
в алгебраической форме имеет вид … |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
Варианты ответов: 1) |
2) |
|
|
|
3) |
|
|
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Решение. Если комплексное число |
|
записано в показательной форме |
|
|
, то |
||||||||||||||||||||||||||||||||||||||
в алгебраической форме оно имеет вид |
|
|
|
|
|
|
, где |
|
|
|
|
|
|||||||||||||||||||||||||||||||
Так как по условию |
|
|
|
|
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Следовательно, |
|
|
|
|
|
|
Это число из ответа 4). |
|
|
|
|
|
|||||||||||||||||||||||||||||
Задание 27. Определитель |
|
|
|
|
|
|
|
равен … |
|
|
|
|
|
||||||||||||||||||||||||||||||
Варианты ответов: 1) |
|
|
2)1; 3) |
|
|
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Решение. Известно, что |
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Воспользовавшись |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
этим, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответом |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
является комплексное число 3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
18

|
Задание 28. Если |
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
, то частные |
|
|
|
|
равно … |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Варианты ответов: 1) 2 |
|
|
2) 18 |
|
|
|
|
|
; 3) 2; |
4) 3 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
Решение. |
Если |
|
|
|
|
и |
, |
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как в данном |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
примере |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частное |
|
|
|
|
есть |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
комплексное число 1). Отметим, что в алгебраической форме оно имеет вид |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
(см. задание 26). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Задание 29. При вычислении числа |
|
|
|
|
|
|
по формуле Муавра получим … |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Варианты ответов: 1) 8; 2) 8i; 3) 16; 4) 8+8i. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
Решение. |
Представим |
число |
|
|
|
в тригонометрической форме. Так как |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
то |
|
|
|
|
|
|
Угол |
|
определяется из равенств: |
|
|
|
|
|
|
|
|
|
В |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
данном случае эти равенства имеют вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и, следовательно, |
|
|
Тогда |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если |
|
|
|
|
|
|
, |
|
|
|
то по |
формуле Муавра |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
. Применяя |
|
эту формулу, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответом является число 3). |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
Задание 30. Спектром линейного преобразования |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
является множество чисел … |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Варианты ответов: 1) |
|
|
|
|
2) |
|
|
|
|
|
|
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Решение. |
Матрица А этого преобразования имеет вид |
|
|
|
|
|
|
|
|
Множество |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
характеристических корней называется спектром линейного преобразования (спектром
матрицы А). |
Характеристические корни векового уравнения |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
т.е. алгебраического уравнения второй степени относительно прямой λ |
|
|
||||||||||||||||||
|
||||||||||||||||||||
или |
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
Корнями является сопряжённая пара |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
комплексных |
чисел |
|
и |
|
|
|
|
|
|
|
|
|
. Совокупность этих двух комплексных |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
чисел и есть спектр данного линейного преобразования, т.е. множество 3).
19
