
5694
.pdfМинистерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Хабаровская государственная академия экономики и права»
Кафедра математики и математических методов в экономике
Математический анализ
Числовые последовательности и их приложения
Учебное пособие
Хабаровск 2008
2
УДК 517.51
ББК Т 45
Ломакина Е. Н., Тиунчик М. Ф. Математический анализ. Числовые последовательности и их приложения : учеб. пособие. – Хабаровск : РИЦ ХГАЭП, 2008. – 104 с.
Рецензенты:
Кондратьев А. И., зав. каф. прикладной математики ДВГУПС, доктор технических наук, профессор Чеботарёв В. И., зав. лаб. ВЦ ДВО РАН, доктор физ.-мат. наук, профессор
Утверждено издательско-библиотечным советом академии в качестве учебного пособия
©Ломакина Е. Н., Тиунчик М. Ф., 2008
©Хабаровская государственная академия экономики и права, 2008
|
3 |
|
Содержание |
Введение................................................................................................................. |
4 |
Глава 1. Множества..…………………………………………………………….5 |
|
Упражнения………………..…………………………………….........12 |
|
Глава 2. Числовые последовательности………..………………………..........19 |
|
Упражнения…………………………..………………………….........30 |
|
Глава 3. Теория пределов последовательностей…..………………………….34 |
|
3.1.Определение предела последовательности…..…………………....34
3.2.Бесконечно большие последовательности…..…………………….38
3.3.Бесконечно малые последовательности и их свойства……..…….41
3.4.Основные свойства сходящихся последовательностей……..…....46
3.5.Предел суммы, произведения, частного и
степенно-показательного выражения…………………………….48
3.6. Особые случаи и неопределённые выражения…..………………..50 3.7. Предельный переход в равенстве и неравенствах…..........……….54
3.8.Пределы монотонных последовательностей………..…………….56
3.9.Принцип стягивающихся отрезков…………..…………………….59
3.10. Число Эйлера е ………………………..…………………………...60
3.11.Некоторые приложения понятия предела……..…………………65 3.12. Определение и основные свойства
подпоследовательностей………………………………………....66
3.13. Критерий Коши………………………………………………….....69 Упражнения………………………………………………………71
Глава 4. Арифметическое n-мерное пространство…………………………....79
4.1.Определение арифметического n-мерного пространства..……….79
4.2.Последовательности точек пространства R n и их пределы…..….83
4.3.Некоторые геометрические вопросы пространства R n ………...…88
4.4.Ограниченные, открытые, замкнутые, связные и
выпуклые множества в пространстве Rn………………………..92
Упражнения………………..……………………………………….100
4
Введение
Учебное пособие соответствует государственному стандарту дисциплины «Математический анализ» для студентов специальности «Математические методы в экономике». Оно может быть использовано для экономических специальностей с углубленным изучением общего курса математики (экономическая теория, антикризисное управление, экономика труда, статистика).
Впособии подробно изложена теория пределов последовательностей
водномерном и n-мерном арифметических пространствах. Имеются некоторые приложения, в том числе экономического содержания. Теоретические положения и выводы иллюстрируются n примерами. Имеется значительный набор упражнений для закрепления изучаемого материала на практических занятиях и при самостоятельной работе.
Фактически пособие является введением в математический анализ, и будет применяться в теории пределов функций одной и многих переменных, в теории рядов, дифференциальном и интегральном исчислениях.

5
Глава 1. Множества
В математике при формулировке определений и теорем используют-
ся слова «существует», «существует единственный», «для любого» и др.;
для краткости записи вместо этих слов будем использовать логические символы (знаки):
–существует, найдётся;
!– существует единственный;
–любой, всякий, каждый;
–следует, влечёт за собой;
–равносильно, тогда и только тогда, необходимо и достаточно;
–принадлежит;
|
|
или – не принадлежит. |
|
|
Символ |
называется квантором существования, |
а символ |
– |
|
квантором общности. При отрицании утверждения знак |
меняется на |
|||
знак , а |
– на знак . |
|
|
|
Одним из исходных и неопределяемых понятий в математике является понятие множества. Создатель теории множеств Георг Кантор дал следующее определение: «Множество (совокупность, семейство) – это собрание определённых и различных объектов нашей интуиции или интеллекта, мыслимое в качестве целого. Объекты, составляющее множество, называются его элементами».
Запись x X означает, что элемент x принадлежит множеству X ( x входит в множество X ). Определённое (конкретное) множество будет считаться заданным, если относительно любого элемента (объекта, предмета) верно одно и только одно их двух утверждений: либо этот элемент входит в данное множество, либо не входит (элемент не принадлежит этому множеству).
Множества задаются двумя способами: либо с помощью перечисления элементов данного множества, либо с помощью указания характеристического свойства элементов этого множества. Множество X , состоящее из элементов x , обладающих свойством P , обозначается
|
Х |
х : Р . |
Множество, не содержащее элементов, называется пустым и обозна- |
||
чается символом |
. |
|
Множество называется конечным, если можно говорить о числе его элементов, т.е. если количество элементов можно выразить каким-то целым положительным числом. В противном случае оно называется бесконечным множеством. У пустого множества число элементов равно нулю.
Определение 1. Множество X называется подмножеством множе-

6
ства Y ( X содержится в Y или X является частью Y ), если
|
|
x |
X |
x Y |
|
(при этом применяется обозначение X |
Y или Y |
X ). |
|||
Условимся, что |
X для любого множества X . |
||||
Определение 2. Множества X и Y называются равными (X Y ) , ес- |
|||||
ли одновременно |
|
|
|
|
|
|
|
X |
Y и Y |
X , |
|
т.е. если множества состоят из одних и тех же элементов. |
|||||
Запись X |
Y не исключает, что X совпадает с Y . |
||||
В дальнейшем будут использоваться операции (действия) объедине- |
|||||
ния и пересечения множеств. |
|
|
|
||
Определение |
3. |
Объединением (соединением, |
суммой) двух мно- |
||
жеств X и Y называется новое множество X Y , состоящее их всех элементов обоих множеств (при этом одинаковые элементы учитываются один раз).
С помощью логических символов объединение двух множеств мож-
но записать в виде |
|
|
X Y |
x : x |
X или x Y . |
Определение 4. Пересечением |
(произведением) двух множеств X |
|
и Y называется множество |
X Y , |
состоящее из общих элементов этих |
множеств, т.е. элементов, принадлежащих как X , так и Y .
С помощью логических символов пересечение двух множеств запишется так:
X Y 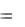 x : x X и x Y .
x : x X и x Y .
В математическом анализе основным рассматриваемым множеством является множество действительных (вещественных) чисел R, которое ещё будем обозначать ( , ) . Строгое построение теории вещественных чисел достаточно сложно.
Множество вещественных чисел R есть объединение множества Q рациональных чисел и множества I иррациональных чисел (R= Q I).
Каждое рациональное число есть либо некоторая конечная десятичная дробь (бесконечная дробь с нулём в периоде), либо бесконечная десятичная периодическая дробь.
Каждому иррациональному числу соответствует некоторая бесконечная десятичная непериодическая дробь.
Будет использоваться геометрическое представление (истолкование, изображение) вещественных чисел. Для этого на некоторой прямой линии выбирается точка O в качестве начала отсчёта, положительное направление и масштабный отрезок OE, длина которого принимается за единицу. После этого выбора прямая называется координатной прямой (числовой прямой или числовой осью). Обычно числовую ось располагают горизон-

7
тально, а за положительное направление берут направление слева направо. Координатную прямую будем обозначать Ox.
Между множеством R всех вещественных чисел и множеством всех точек M координатной прямой Ox имеется взаимно-однозначное соответствие:
1)каждому вещественному числу x соответствует определённая (конкретная) точка M прямой;
2)каждой точке M прямой соответствует некоторое вещественное число x .
При этом число x называют координатой точки M и записывают как M (x) . В связи с этим вещественные числа называют точками. Дей-
ствительные числа (точки) заполняют собой сплошь всю числовую прямую.
Отметим, что точке O (началу координат) приписывается число 0, а точке E – число 1. Различным числам соответствуют различные точки и
наоборот. Абсолютная величина |
x |
координаты x |
точки M есть длина |
|||
отрезка OM (см. рис. 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О(0) |
Е(1) |
M (x) |
x |
|||
Рис. 1 Напомним, что модуль (абсолютная величина) вещественного числа
x определяется следующим образом:
|
|
|
х, если |
х |
0; |
|
|
х |
|
0, |
если |
х |
0; |
|
|
|||||
|
|
|
х, если |
х 0. |
||
Читателю должно быть хорошо известно, что любым x , y R од- |
||||||
нозначно сопоставляется число x |
y |
R, |
называемое суммой чисел x и |
|||
y , а также число xy R, |
называемое их произведением. Эти операции |
|||||
(действия) над числами обладают определёнными свойствами. Кроме того, множество R является линейно упорядоченным. Это означает, что для
x, y R выполнено одно и только одно из соотношений
x y, x y, x y.
Рассмотрим множества, которые будут часто встречаться в дальнейшем изложении и являются подмножествами R. Это, прежде всего, следующие два множества:
1)N 1,2,3,... – множество натуральных чисел,
2)Z ..., 2, 1,0,1,2,... – множество целых чисел.
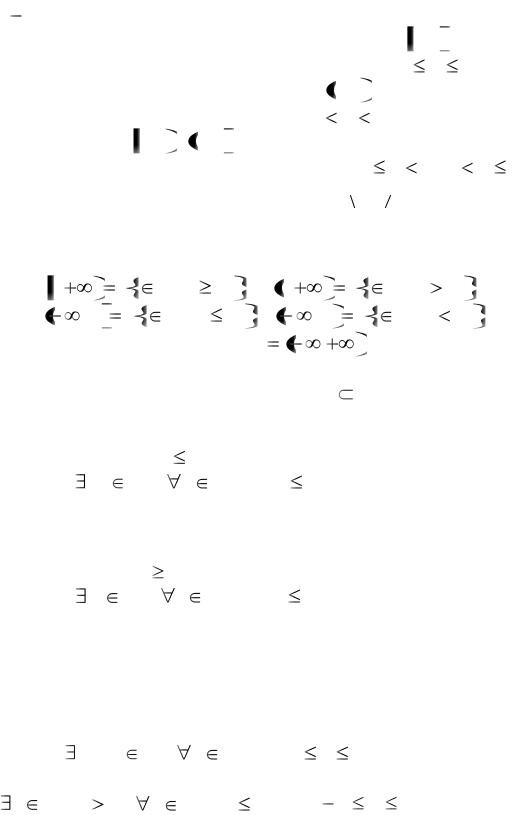
8
Эти множества заданы перечислением элементов.
Будут использоваться следующие промежутки конечной длины
b |
a : |
|
|
|
|
|
|
1) |
отрезок (сегмент, |
замкнутый промежуток) a,b , |
т.е. множе- |
||||
|
ство точек x , удовлетворяющих неравенствам a |
x |
b ; |
|
|||
2) |
интервал (открытый промежуток) |
a,b , т.е. |
множество точек |
||||
|
x , удовлетворяющих неравенствам a |
x |
b; |
|
|
|
|
3) |
полуотрезки a,b , |
a,b , т.е. множества всех точек |
x , |
удовле- |
|||
|
творяющих соответственно неравенствам a |
x |
b, a |
x |
b . |
||
Общее обозначение любого такого промежутка –  a,b
a,b . Каждый промежу-
. Каждый промежу-
ток задан указанием характеристического свойства его элементов. Кроме того, применяются промежутки бесконечной длины (полупрямые или чис-
ловые лучи)
a, |
x R : x a , |
a, |
x R : x a , |
|||
, a |
x R : x a , |
, a |
x R : x a . |
|||
Координатная прямая Ox есть R |
, |
. |
||||
Рассмотрим теперь важные понятия, относящиеся к произвольным |
||||||
непустым множествам X числовой прямой ( X |
R). |
|||||
Определение 5. Множество X называется ограниченным сверху, ес- |
||||||
ли существует такое число M , |
что для любого числа x из множества X |
|||||
выполняется неравенство x |
M , или |
|
|
|||
M |
R |
x |
X |
: |
x M . |
|
Число M в этом случае называется верхней границей множества X . |
||||||
Определение 6. Множество |
X называется ограниченным снизу, если |
|||||
существует такое число m , что для любого числа x из множества X вы-
полняется неравенство x |
m , или |
m R |
x X : m x . |
Число m называется нижней границей множества X .
Очевидно, что для ограниченного сверху множества существует бесконечно много верхних границ, а для ограниченного снизу множества – бесконечно много нижних границ.
Определение 7. Множество X , одновременно ограниченное сверху
и снизу, называется ограниченным, т.е. |
|
|||
M , m R x X : |
m x M . |
|||
Это определение равносильно следующему: |
||||
|
|
|
или c x c . |
|
c R , c 0 |
x X : |
x |
c |
|
|
|
|
|
|
Наименьшая из верхних границ ограниченного сверху множества X называется точной верхней границей этого множества и обозначается sup X , а наибольшая из нижних границ ограниченного снизу множества
9
X называется точной нижней границей этого множества и обозначается inf X . Часто точную верхнюю границу называют верхней гранью, а точную нижнюю границу – нижней гранью.
Введём равносильные определения этих понятий.
Определение 8. Число M * |
sup X есть точная верхняя граница |
множества X , если выполняются следующие два условия:
1) |
x |
X : x |
M *, |
|
2) |
|
0 x' |
X : M * |
x . |
Условие 1) означает, что M * есть верхняя граница для X (одна из верхних границ), а условие 2) – что M *есть наименьшая из верхних гра-
|
|
~ |
M |
* |
уже не является верхней границей (см. рис. 2). |
|||||
ниц, т.е. никакое М |
|
|||||||||
|
|
|
|
x |
|
х |
|
|
|
|
|
|
|
|
х |
|
|
|
|
||
|
|
|
|
|
|
М * |
|
|
||
|
|
|
|
|
M * |
* |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2 |
|
|
|
|
|
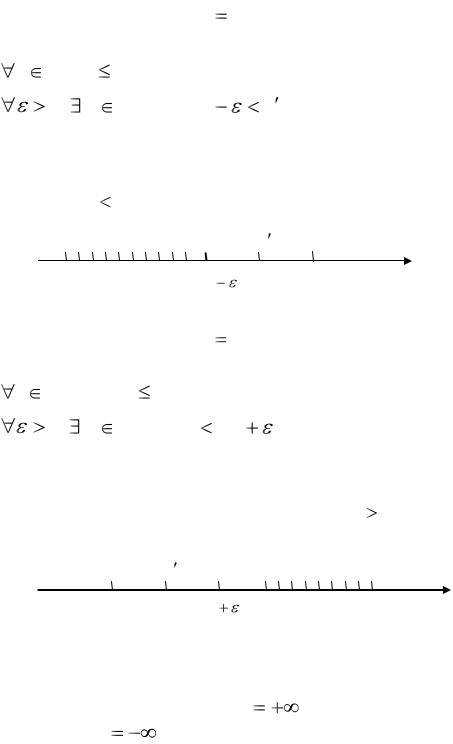
Определение 9. Число m* |
inf |
X |
есть точная |
нижняя граница |
||||||
множества X , если выполняются два условия: |
|
|
||||||||
1) x |
X |
: |
m* |
|
x , |
|
|
|
|
|
2) |
0 x' |
X : x' |
m* |
. |
|
|
|
|||
Условие 1) этого определения означает, что есть нижняя граница |
||||||||||
множества |
X |
(одна |
из |
нижних |
границ), |
а условие 2) |
|
– что m* есть |
||
|
|
|
|
|
|
|
|
~ |
* |
уже не является |
наибольшая из нижних границ, т.е. никакое число m m |
|
|||||||||
нижней границей (см. рис. 3). |
|
|
|
|
|
|||||
|
|
|
|
|
х |
|
|
x |
|
|
|
|
m* |
|
m* |
|
|
|
|
x |
|
Рис. 3 Теорема. Любое непустое ограниченное сверху (снизу) множество
имеет точную верхнюю (точную нижнюю) границу.
Условимся далее писать: sup X |
, если множество X не огра- |
|
ничено сверху; inf X |
, если множество X не ограничено снизу. |
|
Проиллюстрируем понятия этой темы примерами.
Примерами множеств, объединённых по какому-то определённому признаку, являются:
1) множество всех студентов данного института;

10
2)множество всех первокурсников этого института;
3)множество многочленов степени n;
4)множество многочленов степени, не превосходящей n;
5)множество всех прямых, проходящих через фиксированную точку. Первые два множества являются конечными, а три последующих –
бесконечными. При этом второе множество является подмножеством первого, а третье – подмножеством четвёртого.
Пусть X – множество корней уравнения x 2 |
5x 6 |
0 . Очевид- |
|
но, что корнями являются действительные числа x1 |
2 и x2 |
3. Следо- |
|
вательно, X |
2,3 . Множество записано с помощью перечисления его |
||
элементов. Это множество конечно, т.к. состоит из двух элементов. Оно
является ограниченным, при этом inf X 2, sup X |
3. |
|
|
|
|
|
|
|
|
Примером бесконечного множества является Х |
1, |
1 |
, |
1 |
,..., |
1 |
,... . |
||
|
|
|
|
||||||
2 |
3 |
n |
|||||||
|
|
|
|
|
|||||
В этой записи множество задано перечислением его элементов. Хотя все элементы множества не выписаны, но структура его очевидна.
Это множество можно записать с помощью характеристического свойства следующим образом:
X x R : x |
1 |
, n |
. |
|
n |
||||
|
|
|
Данное множество является ограниченным. Верхними границами являются
любые действительные числа |
x 1, |
при этом sup X |
1. Нижними гра- |
||||||||||
ницами будут все вещественные числа x |
0, причём inf X |
0. |
|
||||||||||
|
Примером пустого множества является множество действительных |
||||||||||||
корней уравнения x 2 |
x 1 |
0. |
|
|
|
|
|
|
|
|
|||
|
Пусть Х |
М (х, у) |
Оху : |
ОМ |
|
r |
– |
множество |
точек |
||||
|
|
|
|
||||||||||
M x, y |
на координатной плоскости Oxy, равноудалённых от начала ко- |
||||||||||||
ординат O на фиксированное расстояние r , а Y |
(х, |
у) : х2 |
у2 |
r2 |
|||||||||
– множество пар вещественных чисел |
|
x, y , удовлетворяющих уравнению |
|||||||||||
х2 |
у2 |
r 2 . Эти множества равны |
|
X |
|
Y |
и задают на плоскости в |
||||||
выбранной декартовой прямоугольной системе координат Oxy окруж-
ность радиуса r с центром в начале координат. В приведённых записях X и Y задавались характеристическими свойствами.
Рассмотрим примеры операций над множествами.
Пусть X 1, 2, 3, 4, 5, 6 , Y |
3, 4, 5, 6, 7, 8 . Объединением |
этих множеств будет множество X Y |
1, 2, 3, 4, 5, 6, 7, 8 , а пересе- |
