5694

21

члены x2 , x3 и т.д., полагая в последнем равенстве n 1, 2,.... В более общем случае должна быть формула, по которой при заданных первых

Таким образом, последовательность имеет вид 1, 2, 4,8,16,.... Тогда получается явная формула для общего члена:

хn 2n 1.

Возникает вопрос о переходе от рекуррентного способа задания последовательности к более удобному аналитическому способу. В некоторых ситуациях, выписав по рекуррентной формуле несколько первых членов последовательности, можно уловить закономерность, по которой изменяется

общий член xn при изменении n (так случилось в последнем примере).

число. Такая рекуррентная формула задаёт арифметическую прогрессию с первым членом x1 и разностью прогрессии d . Тогда легко установить явную формулу

xn x1 (n 1)d .

Последовательность, заданная рекуррентной формулой вида xn 1 xnq (n 1, 2,...) ,

22

с известным первым членом x1 называется геометрической прогрессией со знаменателем q . Явный способ её задания такой:

xn qn 1x1 (n 1, 2,...).

Обратимся к геометрической интерпретации последовательностей. Каждую последовательность можно изобразить двумя способами. Первый

способ состоит в том, что каждый член xn последовательности изображается точкой M n на координатной прямой Ox, координатой которой является число xn (см. рис. 4).

x

Рис. 4

Если последовательность стационарна (xn a) , то она изобразится только одной точкой M (a). Если множество чисел, из которых составлена

последовательность, конечно, то она изобразится конечным числом точек на координатной прямой. Например, последовательность

разится бесконечным числом точек. Конечно, все эти точки на Ox мы отметить не сможем, однако наглядное представление о такой последова-

Второй способ изображения последовательности осуществляется с помощью прямоугольной декартовой системы координат Oxy на плоско-

сти. Тогда на такой плоскости отмечаются точки M n с координатами (n, xn ) . Такое изображение можно считать графиком последовательности

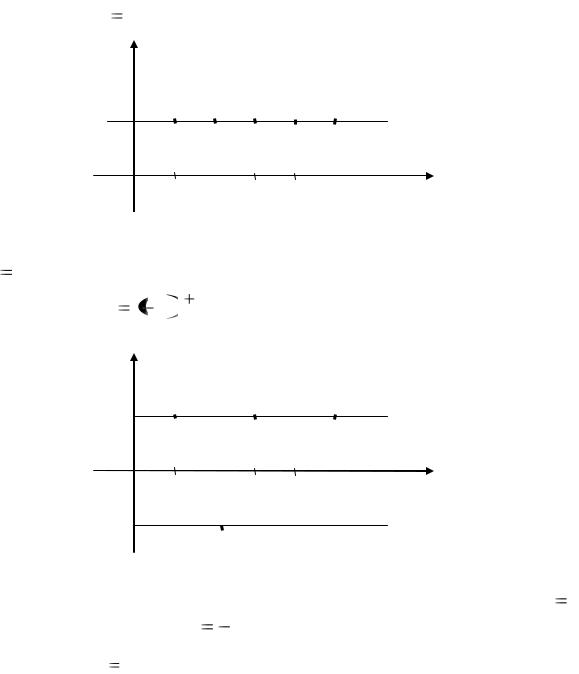
23

как функции натурального аргумента. Все точки M n (n, xn ) изолированы,

т.е. отделены друг от друга. Этих точек всегда бесконечное число, т.к. аргумент n принимает все значения из множества натуральных чисел, которое бесконечно.

Поясним второй способ изображения последовательностей примерами и соответствующими рисунками.

Пусть xn a (см. рис. 6).

y

a

Рис. 6.

Изображено только пять точек. Все точки находятся на прямой

y a . O

В дальнейшем в необходимых случаях общие члены последовательностей

Данное определение означает, что все действия с последовательностями выполняются поэлементно или почленно.

Найдём сумму, разность, произведение и частное последовательностей со следующими общими членами:

1 xn n, yn n .

Согласно определению 2, получим следующее:

25

Общие члены соответствующих последовательностей (суммы, разности, произведения и частного), полученные из данных, таковы:

Проведём простейшую квалификацию последовательностей. Определение 3. Последовательность xn называется ограниченной

сверху, если

МR n N : xn M .

Определение 4. Последовательность xn называется ограниченной снизу,

если

m R n N : xn m .

Определение 5. Последовательность xn называется ограниченной, если она ограничена и сверху и снизу, т.е.

Отрицание определения 6 приведёт к определению неограниченной последовательности, при этом утверждение (неравенство) надо заменить

С0 xn (xn ) : xn C.

Неограниченная последовательность может быть ограниченной или снизу, или сверху, т.е. односторонне ограниченной.

Так как любая последовательность xn может рассматриваться как множество xn , то можно говорить о inf xn и sup xn .

монотонной, при этом последовательности первых двух видов называют

строго монотонными, а двух других – монотонными в широком смысле.

Строго возрастающая последовательность есть частный случай неубывающей, а строго убывающая – невозрастающей.

Не всякая последовательность является монотонной. Например, по-

Последовательность 1, 1, 2, 2, ...,n, n, ... является неубывающей, а

1, 1, 12 , 12 , ..., 1n , 1n ,...– невозрастающей.

Для выяснения вида монотонности можно для всех n установить соответствующее из следующих неравенств:

xn 1 xn 0, xn 1 xn 0 , xn 1 xn 0 , xn 1 xn 0 .

28

При начислении простых процентов долг заёмщика за один период начисления увеличится на величину rS , и к концу второго периода ещё на rS , что составит величину 2rS . Ясно, что к концу срока кредитования долг заёмщика увеличится на

Таким образом, процесс изменения первоначальной суммы S за n периодов при начислении простых процентов описывается арифметической прогрессией с разностью rS :

1 r S, (1 2r)S,..., (1 nr)S.

Следовательно, при простой ставке (постоянной на протяжении всего срока кредитования) формула простых процентов

Sn (1 nr)S

даёт наращенную сумму за n периодов начисления. При этом проценты за весь срок кредитования составят величину

простых процентов описывает решение этого уравнения (от рекуррентного способа задания наращенной суммы Sn перешли к явной формуле).

Поясним формулу простых процентов числовым примером. Пусть банк выдал кредит в размере 50 млн руб. на 3 года при простой ставке

чальная сумма, r – ставка процента за период и n – число периодов наращения. К концу первого периода проценты равны rS , а наращённая сумма

S1 Sn rS (1 r)S и совпадает с наращённой суммой за первый пе-

риод по простым процентам. Далее, согласно определению сложных процентов имеем рекуррентное соотношение

Sn 1 Sn rS или Sn 1 (1 r)S (n 1, 2,...) ,

29

величина S1 уже известна. Легко усмотреть явную формулу для решения

этого уравнения:

Sn 1 r n S ,

которая называется формулой сложных процентов при их дискретном начислении. Величину 1 r n называют множителем наращения сложных процентов. Последовательность (Sn ) , заданная формулой сложных процентов, есть геометрическая прогрессия со знаменателем 1 r и пер-

вым членом 1 r S .

Если банк выдаст кредит в 50 млн руб. на 3 года под 8% годовых по ставке сложных процентов, то к окончанию срока кредита долг заёмщика со-

ставит сумму S3 1 0,08 3 50 62 985 600 руб. Процентные деньги составят 12 985 600 руб.

С помощью последовательностью можно описывать динамические процессы, т.е. процессы, развивающиеся во времени (время считается дискретным). В модулях с дискретным временем ось переменной t разбивается на последовательные равные периоды времени, а каждому периоду по

порядку приписывается номер n . Некоторая последовательность (xn )

как функция натурального аргумента n будет описывать процесс. Только что были изучены две простые модели финансового рынка. Тогда роль

(xn ) выполняла наращённая сумма (Sn ) .

Теперь обратимся к моделям описания динамики популяций. Например, можно изучить изменение во времени населения города (региона, страны). При этом будем предполагать отсутствие катастрофических последствий (в случае населения – войн, стихийных бедствий, эпидемий, вынужденных миграций и т.д.). Естественно, последовательность, описывающая такой процесс, будет положительной. Важными показателями изменения переменной во времени являются темп её прироста и темп роста.

Темпом прироста переменной за промежуток между двумя соседними периодами называется число rn , определяемое равенством

а темпом роста – число

nxn 1 . xn

Очевидно, что n 1 rn .

Рассмотрим случай, если темп прироста постоянен: rn r const

30

при всех n . Тогда темп роста также постоянен, причём

1 r .

ность вида по истечении первого периода при первоначальной численности x0 . Выписанное рекуррентное соотношение означает, что последовательность

(xn ) – геометрическая со знаменателем q 1 r , совпадающим с

темпом роста.

Рассмотренная последовательность записывается в явном виде

Её члены дают численность популяции через n периодов при постоянном темпе прироста r в каждом периоде и первоначальной численности

x0 .

Обратим внимание, что при r 0 при увеличении n величина xn

стремится к нулю. Если же r растёт.

Гипотеза постоянного темпа прироста (например, населения) может применяться только на небольшом отрезке времени (число n периодов не очень велико), иначе можно получить не верные результаты. В литературе имеются более сложные, но и более реалистичные модели динамики популяции.

Упражнения

1. Даны следующие упорядоченные наборы из чисел:

Выясните, какие из них являются последовательностями.

2. Выпишите первые пять членов последовательностей, общие члены которых заданы формулами: