
5694
.pdf
|
91 |
|
|
Определение 7. Множество точек M |
R n , удовлетворяющих усло- |
||
вию |
|
|
|
M , M 0 |
r r |
0 |
(4.14) |
т.е. находящихся на расстоянии |
r |
от точки M 0 R n , называется n - |
|
мерной сферой радиуса r с центром в точке M 0 .
В R3 множество (4.14) есть обыкновенная сфера; в двумерном про-
странстве R 2 это будет окружность, уравнение которой имеет вид x x0 2 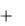 y y0 2 r 2 .
y y0 2 r 2 .
На координатной прямой (в одномерном пространстве R1) это будет множе-
ство x0 r, x0 |
r , |
состоящее из двух точек. Это есть точки пересечения |
||||||
окружности радиуса r с центром в точке M0 (x0, 0) с осью Ox. |
||||||||
Определение 8. Множество точек M |
R n , удовлетворяющих усло- |
|||||||
вию |
|
|
|
|
|
|
|
|
|
|
M , M 0 |
|
r r |
0 |
|
(4.15) |
|
называется n -мерным шаром радиуса r с центром в точке M 0 . |
||||||||
В R3 множество (4.15) есть обыкновенный трёхмерный шар; в R 2 |
||||||||
это будет круг; в R1 это множество будет отрезком x0 |
r, x0 r . |
|||||||
Параллелепипед (4.13) называют замкнутым параллелепипедом, а |
||||||||
шар (4.15) – замкнутым шаром. |
|
|
|
|
|
|||
Множество |
M |
Rn : a |
i |
x |
b |
i |
1,...,n |
называется откры- |
|
|
|
i |
i |
|
|
|
|
тым параллелепипедом, а множество точек, удовлетворяющих строгому неравенству 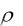 M , M 0 r , называется открытым шаром.
M , M 0 r , называется открытым шаром.
Открытый параллелепипед есть параллелепипед без его граней. На плоскости это будет прямоугольник без его сторон. На координатной прямой это будет отрезок без его концов, т.е. интервал (a, b) .
Открытый шар есть шар без сферы (4.14). На плоскости это будет круг без окружности, а на координатной прямой – интервал
x0 r, x0 |
r . |
|
Смысл открытых и замкнутых множеств будет уточняться в следу- |
||
ющем пункте этой главы. |
||
Определение |
9. Параллелепипедальной окрестностью точки |
|
M 0 x1(0) , ..., |
xn(0) |
называется открытый прямоугольный параллелепипед |

|
|
|
|
|
|
|
92 |
|
|
|
|
|
|
|
x(0) |
|
|
|
|
|
|
|
|
||
M |
Rn : |
x |
|
i |
, (i |
1, ..., n) |
с центром в точке M |
0 |
. |
|
||
|
|
i |
i |
|
|
|
|
|
|
|
||
|
Если все |
i |
, то это будет открытый n -мерный куб (на плоско- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
сти – открытый квадрат со стороной 2 ). |
|
|
|
|
|
|||||||
|
Определение 10. Открытый шар |
(M , M 0 ) |
радиуса |
0 с |
||||||||
центром в точке M 0 x1(0) , ..., |
xn(0) называется шаровой |
-окрестностью |
||||||||||
точки M 0 . |
|
|
|
|
|
|
|
|
|
|
||
|
Если точка M 0 |
окружена окрестностью одного из указанных двух |
||||||||||
типов, то её можно окружить и окрестностью другого типа, содержащейся в первой (являющуюся подмножеством первой). Предоставляем доказать это читателю (например, в двумерном случае).
На координатной прямой |
Ox (пространство R1) прямоугольная |
|||||
окрестность точки характеризуется неравенством |
x x0 |
, а шаровая |
||||
|
x0 |
|
|
|||
окрестность – неравенством |
x |
|
. Оба множества являются одно- |
|||
типными интервалами, а при |
|
эти интервалы даже совпадают. Таким |
||||
образом, в одномерном пространстве понятия параллелепипеидальной и шаровой окрестности точки совпадают.
4.4. Ограниченные, открытые, замкнутые, связные и выпуклые множества в пространстве Rn
Определение 11. Множество M точек M пространства Rn называ-
ется ограниченным, если это множество содержится в некотором параллелепипеде (в некотором шаре).
Любой параллелепипед и любой шар в Rn являются ограниченными множествами.
Из определений 6 и 11 следует, что все координаты любой точки M
ограниченного множества |
удовлетворяют неравенствам ai |
xi bi , где |
ai и bi – фиксированные |
числа. Таким образом, множество |
M ограни- |
чено тогда и только тогда, когда множество значений каждой координаты ограничено как множество точек на координатной прямой.
Так как в определении 11 можно взять шар с центром в начале коор-
динат, |
то из определений 8 и 11 следует, что 0 |
(O, M ) r. Таким об- |
разом, |
у ограниченного множества M расстояния всех его точек до |
|
начала координат ограничены.
Определение 10 применимо, в частности, и к последовательностям

93
(M k ) точек из пространства Rn, так как последовательности можно трак-
товать как множества |
M k . |
|
|
|
|||||
Rn |
Ясно, что не всякая ограниченная последовательность точек M k из |
||||||||
является |
сходящейся. |
Например, |
последовательность точек |
||||||
M k |
1 к 1, |
1 |
является ограниченной, так как все точки M k находятся |
||||||
К |
|||||||||
|
|
|
|
|
|
|
|
||
в прямоугольнике П |
M |
R2; |
2 |
x1 |
2, 0 x2 2 . Но так как по- |
||||
следовательность x1(k ) |
( |
1)k |
1х1(к) |
не имеет предела, то и последова- |
|||||
тельность этих точек M k предела не имеет.
Нетрудно доказать, что если последовательность точек сходится к некоторой предельной точке, то эта последовательность ограничена (см. аналогичную теорему 7 из главы 3 для одномерного пространства R1).
Ломаной в Rn называют множество точек, состоящее из соединённых друг с другом отрезков (см. пункт 4.3) таких, что началом следующего является конец предыдущего отрезка.
Определение 12. Множество M пространства Rn называется связ-
ным, если две любые его точки можно соединить ломаной, все точки которой принадлежат этому множеству.
Примерами связных множеств на координатной прямой являются промежутки a, b .
Примерами связных множеств на плоскости являются вся плоскость, прямоугольник, круг и любая «фигура», не распадающаяся на отдельные, не соединённые между собой части.
Определение 13. Точка M 0 M называется изолированной точ-
кой этого множества, если можно указать такую окрестность этой точки, в
которой нет точек множества M , отличных от M 0 . |
|
||||
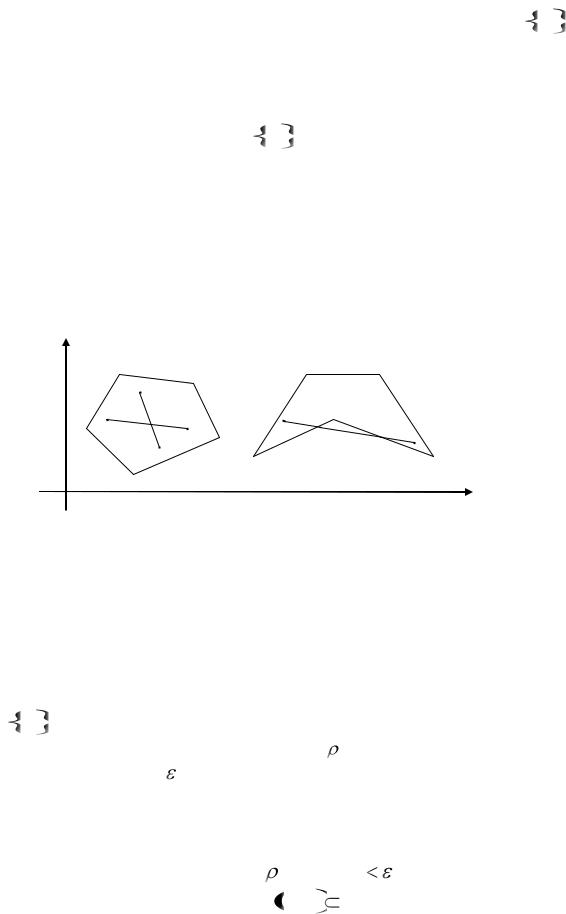
На рис. 14 изображено множество |
M |
, являющееся объединением |
|||
~ |
( M |
|
~ |
M 0 |
). |
множества М и одной точкой M 0 |
|
М |
|||
у |
|
|
|
|
|
|
~ |
|
|
|
|
|
М |
|
|
М0 |
|
|
|
|
|
|
|
|
|
|
|
|
х |
Рис. 14
94
Точка M 0 является единственной изолированной точкой множества M .
Если множество состоит из конечного числа точек, то все его точки будут изолированными.
Если множество имеет хотя бы одну изолированную точку, то оно является связным (см. рис. 14).
Определение 13. Множество M в пространстве Rn называется вы-
пуклым, если вместе с любыми двумя его точками оно содержит отрезок, их соединяющий.
Всё пространство, полупространство, шар, параллелепипед, прямая, луч, отрезок, точка есть выпуклые множества.
На плоскости некоторые многоугольники представляют собой примеры выпуклых множеств, однако не все (см. рис. 15). Многоугольник слева на этом рисунке является выпуклым множеством, а справа – нет. Часть
точек отрезка M1M2 второго многоугольника ему не принадлежит.
у
М1 |
|
М2 |
М1 |
М1 |
М2 |
М2 |
|
х
0
Рис. 15
Любое выпуклое множество в n -мерном пространстве является связным (это следует из определений этих множеств). Однако не всякое связное множество является выпуклым. Действительно, многоугольник, изображённый справа на рис. 15, очевидно, является связным множеством, но не выпуклым, как пояснено выше.
Определение 15. Точка M 0 называется внутренней точкой множества M в n -мерном пространстве, если она принадлежит этому множеству вместе с некоторой своей окрестностью (M , M0 )  (возможно, до-
(возможно, до-
статочно малого радиуса ).
В этом определении можно было иметь в виду и параллелепипедальные окрестности точки M 0 , введённые в определении 8.
Каждая точка пространства Rn является внутренней точкой этого
пространства. Все точки окрестности |
(M , |
M 0 ) |
точки M 0 являются |
внутренними. Любая точка интервала |
a, b |
R1 является его внутренней |
|
точкой.

|
|
|
|
|
|
95 |
|
|
|
|
|
|
Определение 16. Множество |
M |
Rn называется открытым, если |
||||||||
все точки этого множества являются его внутренними точками. |
|||||||||||
|
Всё пространство Rn есть открытое множество, окрестность любой |
||||||||||
точки |
в |
Rn |
есть |
открытое |
множество. |
Параллелепипед |
|||||
M |
Rn : a |
x |
b (i 1, ..., n) |
и шар |
(M , M |
0 |
) |
r |
в Rn являются от- |
||
|
|
i |
i |
i |
|
|
|
|
|
|
|
крытыми множествами. Интервал |
a, b |
R1 является открытым множе- |
|||||||||
ством. |
Отрезок |
a, b |
R1 не является |
открытым |
множеством; точки |
||||||
x |
a и x |
b не являются его внутренними точками. |
|
|
|||||||
Определение 17. Точка M 0 называется предельной точкой или точ-
кой сгущения множества M Rn, если в любой окрестности этой точки имеется хотя бы одна точка множества M , отличная от самой точки
M 0 .
Отметим, что сама предельная точка M 0 может принадлежать, а может и не принадлежать множеству M .
Например, в одномерном пространстве точки a и b являются предельными точками интервала a, b , однако обе самому интервалу не принадлежат. С другой стороны, точки a и b являются предельными для отрезка a, b и обе ему принадлежат.
Множество, состоящее из конечного числа точек, не имеет ни одной предельной точки.
Любая внутренняя точка множества M из Rn является предельной точкой этого множества.
Любая точка из Rn является предельной точкой этого пространства. Все точки параллелепипеда (4.13) являются его предельными точка-
ми; все точки шара (4.15) также являются предельными точками этого множества.
Определение 18. Множество M |
Rn называется замкнутым, если |
ему принадлежат все его предельные точки.
При этом, по определению, множество, не имеющее ни одной предельной точки, также считается замкнутым.
Всё пространство Rn (в частности, R1 или множество ( , |
)) |
является замкнутым множеством.
Параллелепипед (4.13) и, в частности, отрезок a, b одномерного
пространства есть замкнутые множества. Шар (4.15) является замкнутым множеством.
Теперь получено объяснение названиям замкнутые и открытые параллелепипеды, замкнутые открытые шары, применявшиеся а предыдущем
96
пункте.
Имеются множества, которые не являются ни открытыми, ни замкнутыми. Простейшими примерами таких множеств являются полуотрез-
ки a, b и a, b координатной прямой.
Напомним ещё, что в главе 1 отрезок a, b назывался замкнутым промежутком, а интервал a, b – открытым промежутком, чему и дано
– открытым промежутком, чему и дано
объяснение в этом пункте.
Введём ещё два важных определения – понятия граничной точки множества и границы множества.
Определение 19. Точка M 0 из Rn называется граничной точкой множества M Rn, если каждая окрестность этой точки имеет, как точки множества M , так и точки, не принадлежащие этому множеству.
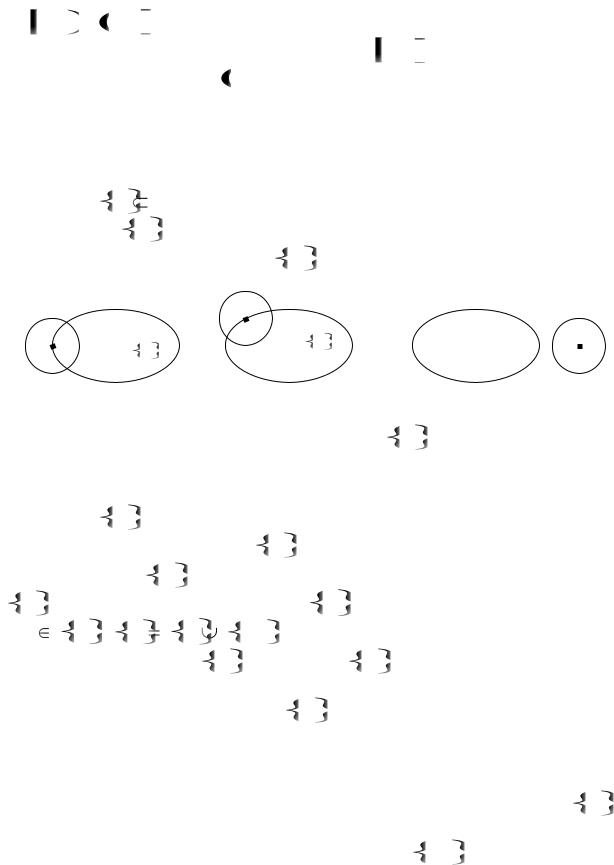
Граничные точки M 0 для M в двумерном пространстве R2 изоб-
ражены на рис. 16.
M0
M0 |
M |
M |
|
|
~ |
M0 |
М |
|
Рис. 16
На рисунке 16 для каждого множества M изображено по одной граничной точке M 0 . На левом рисунке точка M 0 является и предельной точкой этого множества, и принадлежащей этому множеству. При этом
множество |
M является замкнутым. На среднем рисунке граничная точка |
||||
M 0 |
является предельной для M , но не принадлежит этому множеству; |
||||
само множество |
M является открытым. На правом рисунке множество |
||||
M |
|
|
|
~ |
и одной изолированной точки |
есть объединение множества М |
|||||
M 0 |
M |
|
~ |
M 0 ). Граничная точка M 0 не является пре- |
|
( M |
М |
||||
дельной для множества |
M . Множество |
M правого из рисунков 16 яв- |
|||
ляется замкнутым. |
|
|
|||
|
Граничная точка множества M не обязана быть точкой этого мно- |
||||
жества (средний из рисунков 16). Все рисунки показывают, что граничная точка некоторого множества не может быть одновременно его внутренней точкой.
Определение 20. Множество всех граничных точек множества M называется границей этого множества.
Границу как множество принято обозначать дM .

97
Граничных точек у пространства Rn нет (в частности, одномерное пространство R1 или множество ( ,  ) не имеет граничных точек). Следовательно, у пространства Rn нет границы. Из определения ограниченного множества непосредственно следует, что пространство Rn – множество неограниченное.
) не имеет граничных точек). Следовательно, у пространства Rn нет границы. Из определения ограниченного множества непосредственно следует, что пространство Rn – множество неограниченное.
Обратимся к пространству R1. Граничными точками интервала a, b являются только точки a и b . Граница этого множества есть множество a, b , состоящее из двух точек. Граница самому множеству не принадлежит, а множество является открытым. Граничными точками отрезка a, b также являются только точки a и b . Граница состоит из этих
двух точек; граница принадлежит самому множеству, а множество является замкнутым.
Необходимо различать пределы последовательностей (M k ) и предельные точки последовательности как множества M k . Здесь возможны
разные ситуации, которые поясним ниже на примерах в случае одномерного пространства.
Рассмотрим последовательность 0, 1, 0, 1, ...; она не имеет предела (расходится). Эта последовательность как множество есть 0, 1 , т.е. состоит из двух точек 0 и 1. Множество 0, 1 не имеет предельной точки.
Пусть последовательность стационарна : a, a, a, ..., т.е. |
xk a. |
Тогда lim хк а. Эта последовательность как множество есть |
a , т.е. |
к |
|
состоит из одной точки на координатной прямой. Это множество не имеет предельной точки.
|
Пусть |
хк |
( 1)к |
1 |
; эта последовательность предела не имеет. |
||
|
|
||||||
|
|
|
|
к |
|||
Предельными же точками множества { ( 1)к |
1 |
, К N} будут две точки |
|||||
|
|||||||
|
|
|
|
|
|
к |
|
x |
1 и x |
1. Точки этого множества будут «сгущаться» у точек 1 и 1 |
|||||
(предоставляем убедиться в этом читателю, отметив на оси Ox, например, десять точек этой последовательности). В этом примере ситуация объясня-
ется следующим образом. Если М 0 |
lim М к , то все члены последова- |
|
к |
тельности (M k ) , начиная с некоторого номера K ( ) , должны находиться
в окрестности (M k , M 0 ) |
. Если M 0 – предельная точка множества |
|
M k , то в окрестность (M k , M 0 ) |
должны попадать точки этого |
|
множества, хотя, быть может, и не все точки с номерами K K ( ).

|
|
|
98 |
|
|
|
|
|
|
|
Возьмём последовательность с общим членом хк |
1 |
, предел кото- |
||||||||
|
||||||||||
|
|
|
|
к |
|
|
|
|||
рой равен 0 |
. Эта последовательность как множество есть |
1, |
1 |
, |
|
1 |
,... . Это |
|||
|
|
|||||||||
|
|
|
|
2 |
|
3 |
|
|||
множество |
имеет |
предельную |
точку x0 0. Действительно, любая |
|||||||
окрестность |
( , |
) точки x0 |
0 содержит хотя бы одну точку этого |
|||||||
множества. |
|
|
|
|
|
|
|
|
|
|
Выше отмечено, что у множеств, состоящих из конечного числа точек, предельных точек быть не может. Но не всякое бесконечное множе-
ство имеет предельные точки. Например, множество N натуральных чисел предельных точек не имеет, так как все его точки изолированные. В связи с этим естественно установить критерий, выделяющий класс бесконечных множеств, имеющих предельные точки.
Теорема 2 («принцип Больцано-Вейерштрасса»). Всякое бесконечное ограниченное множество в пространстве Rn имеет хотя бы одну предельную точку.
Доказательство. Ограничимся случаем множества M одномерного пространства. Так как множество ограничено, то можно указать отрезок
a1, b1 |
, содержащий множество M |
(см. главу 1). Разделим отрезок |
|||||
a1, b1 |
пополам. Так как множество |
M бесконечно, то хотя бы одна из |
|||||
двух половин отрезка |
a1, b1 |
имеет бесконечное число точек из M . |
|||||
Обозначим эту половину a2 , |
b2 . Отрезок a2 , |
b2 |
вновь разделим по- |
||||
полам и через a3, b3 |
обозначим ту его половину, которая содержит бес- |
||||||
конечное число точек из множества |
M . Продолжая процесс, получим |
||||||
последовательность вложенных отрезков |
|
|
|
||||
|
a1, b1 |
a2 , b2 |
a3, b3 ... |
an , |
bn |
..., |
|
где каждый последующий составляет половину предыдущего и содержит бесконечное подмножество точек множества M .
Так как
b |
a |
n |
b1 |
a1 |
, |
|
|
||||
n |
|
2n |
1 |
|
|
|
|
|
|
то рассмотренная система отрезков является стягивающейся. Следовательно, то теореме 17 главы 3 существует единственная точка M 0 (x0 ), общая для всех отрезков an , bn . Покажем, что эта точка является предельной

|
|
|
|
99 |
|
|
|
для множества |
M . Для этого возьмём любой интервал x0 |
, x0 |
|||||
длины |
0 с |
центром |
в точке |
x0 . Если n достаточно |
велико, то |
||
an , bn . Так как отрезок |
an , bn |
содержит бесконечное число точек из |
|||||
множества |
M , то в интервале |
x0 |
, x0 |
имеется бесконечное |
|||
множество точек из M ; |
следовательно, точка x0 |
есть предельная точка |
|||||
множества M , что и требовалось доказать.
При доказательстве этой теоремы в пространстве Rn надо исходить из того, что ограниченное множество содержится в некотором n -мерном исходном параллелепипеде П1. Далее надо строить систему вложенных параллеле-
пипедов Пn делением каждого ребра пополам; при этом в системе будут те параллелепипеды, которые содержат бесконечно много точек из M . Останется устанавливать, что система вложенных параллелепипедов имеет общую точку M 0 , которая и будет предельной для M .
При изучении функций часто применяется понятие «область». Под областями в соответствующем пространстве понимают множества без изолированных точек. Так, множества a, b c и a, b c одномерно-
го пространства, где точка c не принадлежит соответствующему промежутку, областями не называют. Для областей, как и для множеств, вводятся понятия : область ограниченная, открытая, замкнутая, связная, выпуклая. Ограничимся рассмотрением понятий открытая и замкнутая области. Остальные понятия для области читатель должен ввести самостоятельно по аналогии с соответствующими понятиями для произвольных множеств.
Множество, полностью состоящее из внутренних точек, называют
открытой областью.
Примерами открытых областей служат: интервал a, b на координатной прямой, открытый круг (M k , M0 ) r и открытый прямоуголь-
ник на плоскости.
Частным случаем замкнутого множества является замкнутая область. Замкнутой областью называется любое множество, все точки которого являются его предельными точками.
Примерами замкнутых областей являются: отрезок a, b на координатной прямой, а на плоскости – круг (M k , M 0 ) r вместе с точками
ограничивающей его окружности, прямоугольник с включёнными точками его сторон.
Полезно сравнить определения замкнутого множества и замкнутой области. Различие этих определений поясним примерами. Множество a, b c (точка c не принадлежит a, b ) является замкнутым, т.к. со-

100
держит все свои предельные точки, которыми являются точки отрезка a, b . Это множество не является замкнутой областью в одномерном про-
странстве, т.к. точка c , принадлежащая этому множеству, не является его предельной точкой, хотя и является граничной точкой множества.
Обратимся к областям, имеющим так называемые проколотые точки. Рассмотрим на координатной прямой проколотые в центре x0 интервал
x0 |
r, |
x0 |
r и отрезок x0 r, |
x0 |
r , где r |
0. Эти области имеют |
|||
по |
одной |
проколотой |
точке |
и |
их |
можно |
записать так: |
||
x0 |
r, |
x0 |
x0, x0 r ; |
x0 |
r, x0 |
x0, |
x0 |
r . |
Первая область |
является открытой, т.к. состоит только из внутренних точек. Вторая область не является ни открытой, ни замкнутой. Действительно, этой области
принадлежат точки x0 r и x0 r , которые не являются её внутренними точками; следовательно, это не открытая область. Эта область не является замкнутой, т.к. в это множество не входит его предельная точка x0 .
С примерами областей на плоскости читатель ознакомится в упражнениях.
Упражнения
1. В следующих случаях по заданным координатам точек M и P найти координаты вектора МР:
1) M (2, |
1), P(4, 5); |
|
2) M (0, 1), |
P(3, 5); |
|
3) M (2, |
2, |
4), P(0, 1, |
1); |
4) M (1, 0, |
2), P(0, 2, 2); |
5) M (2, |
3, 1, |
2), P(0, 1, 3, |
1); |
|
|
6) M (1, |
3, |
0, 2), P( |
4, 3, |
2, 2). |
|
2. По данному вектору МР и известным координатам его начала (точки M ) найти координаты конца этого вектора – точки P :
1) |
МР = ( 1; 3), |
M (1, |
2); |
|
|
|
||
2) |
МР = (4, |
2, |
1), |
M (3, 0, |
2); |
|
||
3) |
МР = (2, |
1, |
3, |
4), |
M (1, |
1, |
2, |
5); |
4) |
МР = (1, |
2, |
0, |
1), M (3, |
2, |
4, |
5). |
|
3. По данному вектору МР и известным координатам точки P найти |
||||||||
координаты точки M : |
|
|
|
|
|
|
||
1) |
МР = (2, |
4), P(0, |
2); |
|
|
|
||
