
5691
.pdf
81
M1, M 2 , M 3 (аксиома треугольника).
Обратимся к курсам линейной алгебры и аналитической геометрии, в которых изучаются конечномерные векторные пространства.
Упорядоченный набор из n действительных чисел x1,..., xn называ-
ется |
|
арифметическим |
n -мерным |
вектором |
и |
обозначается |
|||||
a |
x1,..., xn |
. Числа |
xi i |
1,..., n называются координатами (иногда |
|||||||
компонентами) вектора a . |
Если у n -мерного вектора все координаты |
||||||||||
равны нулю, то вектор называется нулевым : |
a |
0,...,0 . Два n -мерных |
|||||||||
вектора |
a |
x1,..., xn |
и b |
y1,..., yn |
называются равными (записы- |
||||||
вают a |
b ), если xi |
yi (i |
1,..., n) . |
|
|
|
|
|
|||
|
Над вектором вводятся операции (действия) сложения векторов и |
||||||||||
умножения вектора на действительное число. |
|
|
|
|
|||||||
|
Суммой двух n -мерных векторов a |
|
x1,..., xn |
и b |
y1,..., yn |
||||||
называется вектор |
|
|
|
|
|
|
|
|
|||
|
|
|
a |
b |
xi |
y1,..., xn |
yn . |
|
|
||
|
Произведением вектора a |
x1,..., xn |
на |
действительное число |
|||||||
называется вектор
a  x1,..., xn .
x1,..., xn .
Множество всех n -мерных векторов с действительными координатами, рассматриваемое с определёнными в нём операциями сложения векторов и умножения вектора на действительное число, называется n -
мерным векторным пространством (его также обозначим R n ).
Каждая операция над такими векторами имеет свои свойства (например, a b b a ,  a
a 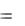 a ). Кроме того, есть два свойства, описывающие связь двух операций между собой:
a ). Кроме того, есть два свойства, описывающие связь двух операций между собой:
1) |
a b |
a |
b, |
2) |
a |
a |
a . |
Всё сказанной означает, что R n представляет собой линейное прост- |
|||
ранство, |
причём конечномерное ( n – размерность этого пространства). |
||
Подробно теория линейных пространств (в частности, n -мерного векторного пространства R n ) излагается в литературе по линейной алгебре 1).
1См. следующие учебные пособия и приведённую в них литературу:
1.Тиунчик М. Ф. Элементы линейной алгебры и аналитической геометрии. Ч. 1. : учеб. пособие. Хабаровск : ХГАЭП , 1996. 128 с.
2.Тиунчик М. Ф. Элементы линейной алгебры аналитической геометрии. Ч. 2. : учеб. пособие. Хабаровск : РИЦ ХГАЭП, 1997. 140 с.
3.Тиунчик М. Ф. Руководство к решению задач по линейной алгебре и аналитической геометрии. Ч. 1. : учеб. пособие. Хабаровск : ХГАЭП, 2001. 132 с.

|
82 |
|
Число a,b , определяемое равенством |
|
|
a, b |
x1 y1 ... xn yn |
(4.3) |
называется R n скалярным произведением векторов a и b . Векторное пространство со скалярным произведением (4.3) называется евклидовым
(гильбертовым) n -мерным векторным пространством. Это позволяет
строить геометрию R n с использованием углов. Угол между векторами определяется по формуле
|
|
|
a, b |
||||
cos |
|
|
|
|
|
|
. |
|
|
|
|
|
|
||
|
|
(а, a) |
(b, b) |
||||
|
Линейное пространство L называется нормированным, если любому |
||||||
вектору a из L может быть поставлено в соответствие число a , называется нормой (длиной) вектора a и удовлетворяющее условиям:
1) |
|
a |
|
0 , если a |
0; |
0 |
|
0 ; |
||||||||||
2) |
|
|
a |
|
|
|
|
|
|
|
a |
|
|
|
a L и |
R ; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3) |
|
a |
b |
|
a |
|
|
b |
|
a,b |
L . |
|||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторное пространство R n |
оказывается |
нормированным, если |
норму |
||||||
определить по формуле |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
||
|
a |
|
|
(a, a) |
x2 . |
(4.4) |
|||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
i |
1 |
|
|
Таким образом, в R n , как и в геометрических пространствах R1 (коорди-
натная прямая), R 2 (плоскость) и R3 (трёхмерное пространство), измеряются длины векторов по формуле (4.4).
Положим по определению
a,b |
a b |
. |
(4.5) |
|
|
|
|
Легко проверить (предоставляем это читателю), что расстояние между элементами (векторами), введённое по формуле (4.5), удовлетворяет перечисленным в этом пункте аксиомам метрического пространства. Отсюда следует, что нормированное пространство является метрическим. Таким
образом, в R n можно измерять расстояния между векторами.
Так как в R n |
a b |
x |
y ,...,x |
n |
y |
n |
, то из (4.4) и (4.5) сле- |
|
|
1 |
1 |
|
|
дует, что
4.Тиунчик М. Ф. Руководство к решению задач по линейной алгебре и аналитической геометрии. Ч. 2. : учеб. пособие. Хабаровск : РИЦ ХГАЭП, 2004. 172 с.

83
|
|
n |
a,b |
(xi yi )2 |
|
|
i |
1 |
(сравните это равенство с (4.1)).
4.2. Последовательности точек пространства R n и их пределы
Будем говорить, что имеется последовательность M k  точек M k
точек M k
из пространства R n , если по некоторому правилу (закону) каждому нату-
ральному числу k(k |
) ставится в соответствие единственная опреде- |
|
лённая точка M k |
R n . |
|
Следовательно, последовательность точек пространства R n есть от- |
||
ражение множества |
всех натуральных чисел в пространство R n . |
|
Подробно последовательность M k запишется так: |
||
|
|
M1, M 2 ,..., M k ,.... |
Точки называются членами этой последовательности. Отметим, что в |
||
R n каждая такая точка имеет n координат. |
||
Точку M k |
называют общим членом последовательности M k . |
|
Последовательность точек будем считать заданной, если будет указана
формула для координат общего члена M k |
x1k ,..., xnk . |
Если каждому натуральному числу |
K будет поставлена в соответ- |
ствие одна та же точка M 0 из R n , |
то получим последовательность |
M 0 , M 0 ,..., M 0 ,..., которую называют стационарной (постоянной). M 0 |
|
в координатной записи выглядит так: M 0 x10 ,..., xn0 . |
|
Обратимся к одномерному пространству R1. Каждая его точка M |
|
характеризуется одной координатой x и записывается M x . Последова-
тельность |
|
M k |
точек |
M k |
R1 |
будет |
иметь |
вид |
||
M x 1 , M |
2 |
x 2 |
,..., M |
k |
x k |
,... или |
x 1 , x 2 ,..., x k |
,.... Последняя |
||
1 |
|
|
|
|
|
|
|
|
||
представляет собой числовую последовательность с общим членом |
x k , |
|||||||||
которые изучались в главе 2. Отметим только, что индекс k |
общего члена |
|||||||||
поставлен сверху. Ранее он писался снизу без скобок и обозначался n , т.е.

84
применялась запись xn . Теперь же индекс n указывает на количество ко-
ординат точки.
Рассмотрим примеры последовательностей точек из конечномерных пространств различных размерностей.
Пример 1. Каждому числу k ставится точка M k |
из R 2 , общий член |
||||||||||
которой имеет вид M k k, |
1 |
|
. Следовательно, имеем последовательность |
||||||||
|
k |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
M1 1,1 , M 2 |
2, |
|
1 |
, M 3 |
3, |
1 |
,..., M k |
k, |
1 |
,... |
|
2 |
|
|
|||||||||
|
|||||||||||
|
|
|
|
3 |
|
k |
|||||
точек из пространства R 2 .
Пример 2. Рассмотрим последовательность двумерных точек с общим членом M k (k, k 2 ) . Это значит, что имеем последовательность точек
|
|
|
M 1,1 , |
M |
2 |
2, 4 , M |
3 |
3,9 ,..., M |
k |
k, k 2 |
,..., |
|
|
|||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
плоскости (пространства R 2 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Пример |
3. |
|
|
|
Рассмотрим |
|
|
последовательность |
точек |
||||||||||||||||||||
M k |
|
1 |
, k, k 2 |
|
R3 . |
Члены этой последовательности имеют следую- |
||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щий вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
M 1,1,1 , |
M |
2 |
1 |
, 2, 4 |
, |
M |
3 |
1 |
, 3, 9 |
,..., |
M |
k |
1 |
, |
k, k 2 ,.... |
|
|||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
|
1 |
|
2 |
|
|
3 |
|
|
k |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Пример 4. Пусть |
|
M k |
|
есть последовательность точек M k |
1 |
из |
|||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
k |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1. Это означает, что имеем числовую последовательность точек |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
M1 1 , M |
2 |
1 |
, |
|
M 3 |
1 |
,..., M k |
1 |
|
,... |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
k |
|
|
||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|||||||||||||||||||||
на координатной прямой Ox . Её можно записать ещё таким образом:
1, |
1 |
, |
|
1 |
,..., |
1 |
,... |
(в краткой записи |
хк |
1 |
); в главе 2 её записывали как |
|||
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||
2 |
|
3 |
k |
|
|
|
k |
|||||||
последовательность с общим членом хn |
|
|
1 |
. Ещё раз подчеркнём, что это |
||||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
одна и та же последовательность. |
|
|
|
|
|
|||||||||
|
|
|
|
Определение 1. Точка |
M 0 |
R n |
называется пределом последова- |
|||||||
тельности |
M k |
точек M k |
R n , если |
|
|
|
|
|||||||

85
lim (М k , М 0 ) 0. |
(4.6) |
k |
|
При этом применяются записи
lim М k М 0, М |
k |
М |
0 |
. |
k |
k |
|
||
При фиксированном k расстояние |
|
является конкретным числом. |
||
С изменением k меняется и это число. Следовательно, в (4.6) речь идёт о пределе числовой последовательности (см. главу 3).
Определение означает, что для любого положительного числа |
су- |
||
ществует номер k k |
, зависящий от |
, такой, что при всех k |
k |
выполняется неравенство |
M k , M 0 |
. |
|
Последовательность точек M k пространства R n называется сходящейся к точке M 0 , если она имеет предел и расходящейся – в противном
случае.
Определение 1 аналогично определению, данному в главе 3 при рассмотрении последовательности точек на прямой. Действительно, каждой
точке M k |
на Ox соответствует некоторое действительное число xk . |
За- |
|||
дание последовательности M k |
точек на прямой равносильно заданию |
||||
числовой последовательности xk |
. Расстояние между точками M k |
xk |
|||
и M 0 x0 |
на прямой определяется равенством (М k , М0 ) |
xk |
x0 |
|
|
(см. пункт 1 данной главы и главы 3). Это и приведёт нас к определению 1 из главы 3.
Можно показать, что сходящаяся последовательность точек имеет только один предел. Очевидно также, что стационарная последователь-
ность M 0 имеет пределом точку M 0 . Рассмотрим примеры на нахождение пределов.
Пример 5.Докажем, что последовательность точек М k |
|
1 |
|
, |
k 2 |
||||||||||||||||||
|
|
k |
k |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
R 2 сходится к точке M0 0,1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Действительно, согласно пункту 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
(М k , М 0 ) |
|
1 |
|
0 |
k 2 |
1 |
|
5 |
|
|
5 |
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k 2 |
|
|
|
|||||||||
|
|
k |
|
|
|
|
|
k |
|
|
|
|
k |
|
|
||||||||
Тогда lim (М k , М0 ) |
|
lim |
5 |
|
|
0. Доказательство завершено, |
|||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
R |
||||||||||||||||||||||
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
установлено равенство (4.6). Пример 6. Доказать, что
из
т.к.

86
lim |
M k |
1 |
, |
1 |
, |
|
k |
1 |
M0 (0, 0, 1). |
|
|
|
|
|
|
|||||||||
|
k |
|
k |
|
|
|
|
|
|
|
||||||||||||||
k |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Применим формулу (4.1) дл нахождения расстояний между точками |
||||||||||||||||||||||||
в пространстве R3 . Получим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
k 1 |
|
|
3 |
|
|
3 |
|
|||||||
(М k , М 0 ) |
0 |
|
|
|
|
|
0 |
|
|
1 |
|
|
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k 2 |
|
|||||||||||
|
|
k |
|
|
|
|
|
k |
|
|
|
k |
|
|
|
|
|
k |
||||||
Так как lim (Мk , М0 ) |
lim |
|
3 |
|
|
0, то равенство (4.6) установле- |
||||||||||
|
|
|
|
|
|
|||||||||||
k |
||||||||||||||||
k |
k |
|
|
|
|
|
|
|
||||||||
но. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 7. Доказать, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
M k |
k |
1 |
|
M0 |
(1). |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
k |
|||||||||||||||
k |
|
|
|
|
|
|
|
|
|
|||||||
Имеем одномерный случай. Тогда |
|
|
|
|
|
|
|
|||||||||
(M k , M 0 ) |
|
|
|
k 1 |
1 |
|
1 |
|
||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
k |
|
k |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и равенство (4.6) очевидно.
По-видимому, читатель из этих примеров заметил, что координаты предельной точки M 0 являются пределами соответствующих координат
точек M k . Этот факт сейчас будет установлен в общем случае пространства
R n .
|
Если задана последовательность точек M k R n |
|
|
|||||||
|
M1 x11 ,..., xi1 ,..., xn1 ,..., M k x1k |
,..., xi k ,..., xnk |
,..., |
|
||||||
то это означает, что имеется n числовых последовательностей: |
|
|||||||||
|
1 |
,..., x k |
|
|
|
|
|
|
|
|
|
x |
,... (последовательность первых координат); |
|
|||||||
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
xi |
1 |
,..., xi |
k |
,... (последовательность i -х координат); |
|
||||
|
|
|
||||||||
|
|
|
|
|
|
|
… |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
xn |
,..., xn k |
,... (последовательность n -ых координат). |
|
||||||
|
Теорема 1 (о координатной сходимости в R n ). Последовательность |
|||||||||
точек |
M |
k |
x k ,..., x k |
,..., x k |
R n |
сходится |
к |
точке |
||
|
|
1 |
|
i |
n |
|
|
|
|
|
M 0 x10 ,..., xi 0 ,..., xn0 |
|
R n ( М k |
М 0 ) тогда и только тогда, когда |
|||||||
|
|
|
|
|
|
|
k |
|
|
|

87
выполняются равенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
lim |
x |
k |
x 0 |
i |
1,..., n . |
|
|
|
(4.7) |
|||||||
|
|
|
|
|
|
|
k |
i |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство необходимости. Дано, что |
lim |
М k |
М 0. Опреде- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
ление 1 означает, что |
lim |
(М k , |
М 0 ) |
0. Для любого i |
1,..., n оче- |
||||||||||||||||||
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
видно неравенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(k ) |
(0) |
|
|
|
(k ) |
(0) |
2 |
|
(k ) |
(0) |
2 |
|
|
(k ) |
(0) 2 |
|
(М k , М 0 ). |
|||||
|
|
|
|
|
|
|
|||||||||||||||||
|
хi |
хi |
|
|
x1 |
х1 |
|
... |
хi |
|
хi |
|
|
... |
хn |
хn |
|
|
|||||
Так как |
lim |
(М k , М 0 ) |
0 , то из предыдущего неравенства следует, |
||||||||||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
что |
lim |
х(k ) |
х |
(0) |
0 . Отсюда следует (4.7). |
|
|
|
|
|
|
||||||||||||
|
|
k |
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство |
достаточности. |
|
Даны |
|
равенства |
(4.7) или |
|||||||||||||||
|
х(k ) |
|
х(0) |
для всех i |
1,..., n . Отсюда следует, что |
|
|
|
|||||||||||||||
|
i |
k |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
(k ) |
|
(0) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(M k , М 0 ) |
|
|
|
х |
х |
|
0, |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
i |
1 |
i |
|
i |
|
k |
|
|
|
|
||
т.е. выполнено неравенство (4.6), |
которое означает М k |
k |
М 0 . Доста- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
точность установлена.
На основании этой теоремы, используя главу 3, находятся предель-
ные точки последовательностей точек из R n . Пример 8. Найдём предельную точку M 0
M k  точек из R3 , заданной общим членом M k
точек из R3 , заданной общим членом M k
для последовательности
1 |
, |
2k |
1 |
, |
k 1 |
. |
|
|
|
|
|||
k |
|
k |
|
|
k |
|
Имеем следующие три числовые последовательности:
х |
(k ) |
1 |
, х(k) |
2k 1 |
, х |
(k) |
k 1 |
. |
1 |
k |
2 |
k |
3 |
k |
|||
|
|
|
|
|
||||
Так как |
|
|
|
|
|
|
|
|
lim х(k) |
lim |
1 |
0, |
lim |
х(k) |
lim |
2k 1 |
2, |
||||
|
|
|
||||||||||
k |
1 |
k |
k |
|
k |
2 |
|
k |
k |
|
||
|
|
|
|
|
|
|||||||
|
|
lim |
х(k) |
lim |
|
k 1 |
1, |
|
|
|
||
|
|
|
|
|
|
|
|
|||||
|
|
k |
|
3 |
k |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
то на основании теоремы имеем, что M 0 0 ,2,1 .

|
|
|
|
|
|
88 |
|
|
|
|
||
|
Если предел хотя бы одной из последовательностей xi |
k |
равен |
|||||||||
бесконечности или вовсе не существует, то последовательность |
M k |
|||||||||||
точек из R n расходится. Это утверждение следует из теоремы 1. |
|
|
||||||||||
|
Пример 9. Исследуем на сходимость следующие последовательности |
|||||||||||
точек из R 2 : |
|
|
|
|
|
|
|
|
||||
1) М |
|
k, |
1 |
; |
2) М |
|
1 |
, ( 1)k 1 ; |
3) М k ( 1)k 1, k 2 . |
|
|
|
k |
|
|
|
|
|
|||||||
|
|
k |
|
k k |
|
|
|
|
||||
|
Все последовательности расходятся. У первой последовательности |
|||||||||||
lim х(k ) |
|
lim |
k |
. У второй – lim |
х(k ) |
lim ( 1)k 1 |
не суще- |
|||||
k |
|
1 |
|
k |
|
|
|
k |
2 |
k |
|
|
|
|
|
|
|
|
|
|
|
||||
ствует (см главу 3). У третьей последовательности предел последовательности первых координат не существует, а предел последовательности вторых координат равен бесконечности.
В пространстве R n также можно ввести определение фундаментальной последовательности.
Определение 2. Последовательность {M k }, |
M k |
R n |
называется |
||
фундаментальной, если для |
0 |
N такое, что для |
k |
N и любо- |
|
го натурального числа m выполняется неравенство |
|
|
|
||
(M k m , M k ) |
. |
|
|
|
|
Теорема 2 (критерий Коши сходимости последовательности). Для |
|||||
того чтобы последовательность {M k }, |
M k R n |
сходилась, необходимо |
|||
и достаточно, чтобы она была фундаментальной.
Доказательство проводится аналогичными рассуждениями теоремы
4.2 пункта 3.13.
4.3. Некоторые геометрические вопросы пространства R n
Введём важные понятия по аналогии с соответствующими понятиями и утверждениями из аналитической геометрии на прямой (одномерном
пространстве R1), плоскости (R 2 ) и в трёхмерном пространстве (R3 ).

|
89 |
|
|
|
|
|
|
Вектором с началом в точке |
M1 x1,..., xn |
и концом в точке |
|||||
P y1,..., yn называется n -мерный вектор |
|
|
|
|
|||
MP |
y1 x1,..., yn |
xn . |
|
|
|||
Вектор OM , где O 0,...,0 – начало координат n -мерного координатного |
|||||||
пространства, называется радиусом – |
вектором точки M . Очевидно, |
||||||
что координаты радиуса – вектора OM совпадают с координатами точки M . |
|||||||
Из сказанного в пункте 1 следует, что |
|
|
|
|
|||
|
|
|
|
|
|||
M , P |
M , P |
, |
O, M |
O, M |
. |
||
Из аналитической геометрии на плоскости и в трёхмерном простран- |
|||||||
стве известно, что уравнение прямой имеет вид |
|
|
|||||
M 0M |
tq |
t |
, |
|
(4.7) |
||
где M 0 – точка, лежащая на этой прямой, |
M – |
переменная (текущая) |
|||||
точка данной прямой, а q – некоторый нулевой вектор, параллельный этой
прямой.
Из определения равных векторов, действий над векторами (см. пункт 1) и уравнения (4.7) в двумерном случае вытекают следующие уравнения:
х х0 |
tg1, |
(4.8) |
|
у у0 |
tg2. |
||
|
|||
Здесь M x, y – текущая точка прямой, M 0 |
x0 , y0 – фиксирован- |
||
ная точка этой прямой, q q1, q2 , |
t |
. Уравнения (4.8) назы- |
|
ваются параметрическими уравнениями прямой на плоскости.
Свойство (4.8) берётся за основу для определения прямой в R n . Определение 3. Множество точек M x1,..., xn  R n таких, что
R n таких, что
M 0M |
|
tq |
t |
, |
(4.9) |
называется прямой в R n , проходящей через точку M 0 x10 ,..., xn0 |
парал- |
||||
лельной вектору q q ,..., q |
n |
R n |
, где q – ненулевой вектор. |
|
|
1 |
|
|
|
|
|
В силу пункта 1 равенство (4.9) приводит к следующим параметри- |
|||||
ческим уравнениям прямой в R n : |
|
|
|
||
х |
|
х(0) |
tg , |
|
|
1 |
|
1 |
1 |
|
|
|
|
..... |
|
|
(4.10) |
|
|
|
|
|
|
xn |
xn(0) |
tgn. |
|
|
|
Определение 4. Множество n -мерных точек, удовлетворяющих условию

|
|
90 |
|
|
|
|
M 0 M |
tq |
t |
, q |
0 , |
(4.11) |
|
называется лучом с началом в точке M 0 . |
|
|
|
|||
Пусть на плоскости заданы две различные |
точки M1 x1, y1 |
и |
||||
M 2 x2 , y2 . Тогда точки M x, y |
отрезка, соединяющего M1 и |
M 2, |
||||
находятся из векторного равенства |
|
|
|
|
||
OM |
1 |
t OM1 |
tOM 2 0 |
t |
1 . |
|
Это равенство достаточно просто установить на основании правила треугольника сложения векторов (надо выразить радиус – вектор OM через
радиусы – векторы OM1, OM 2; для наглядности можно сделать чертёж).
Определение 5. Если M1 |
и M 2 – две различные точки из R n , то |
||||||
отрезком, их соединяющим, называется множество точек |
M R n , удо- |
||||||
влетворяющих равенству |
|
|
|
|
|
|
|
OM |
1 |
t OM1 |
|
tOM 2 0 |
t |
1 . |
(4.12) |
Равенство (4.12) легко записать в координатной форме. |
|||||||
Кроме отрезка, луча и прямой в R n , будут необходимы в дальней- |
|||||||
шем и другие важные множества. |
|
|
|
|
|||
Определение 6. Параллелепипедом (прямоугольным) |
в R n назы- |
||||||
вается множество точек |
M x1,..., xn , координаты которых независимо |
||||||
одна от другой удовлетворяют неравенствам |
|
|
|||||
|
a1 |
x1 |
b1,..., an |
xn |
bn , |
|
|
где ai и bi – фиксированные числа, причём ai |
bi . |
|
|||||
Таким образом, |
|
как множество имеет вид |
|
||||
M |
Rn : a |
x |
b i |
1,..., n . |
(4.13) |
||
|
|
i |
i |
i |
|
|
|
Параллелепипедом в пространстве R1 является отрезок. Параллеле-
пипед в пространстве R 2 всегда является некоторым прямоугольником
(см. рис.13).
x2 b2
а2
а1 |
b1 |
x1 |
Рис. 13
