5691

61

чисел h 1 и всех натуральных чисел n , причём равенство имеет место только в очевидных случаях: h 0 или n 1.

Доказательство проведём методом математической индукции.

При n 1 неравенство (3.13) имеет вид 1 h 1 h и, значит, справедливо вообще для всех значений h . Предположим, что оно справедливо

Знак неравенства после умножения не изменится. В результате получим:

который представляет собой степенно-показательное выражение. Нужно выяснить, является ли последовательность (3.14) сходящейся. Так как

вида 1 (см. пункт 3.6), которую и надо раскрыть.

Так как предел основания равен единице, а показателем является натуральное число, то можно было бы ожидать, что искомый предел равен единице. Однако это не так. Из (3.13) следует, что для любого n справедливо неравенство

и, следовательно, если последовательность (3.14) имеет предел, то lim xn 2 .

Оказывается, что изучаемая последовательность ограничена сверху и монотонно возрастает (непосредственно это не усматривается). Согласно пункту 3.8 (пределы монотонных последовательностей) такая последовательность имеет конечный предел. По предложению Эйлера его принято обозначать буковой e:

Можно доказать (это доказательство опускается), что e является иррациональным числом и, следовательно, представляется в виде бесконечной непериодической дроби. Приведём приближённое значение e с точностью до

пятнадцатого десятичного знака после запятой (с точностью до 10 15):

e2,718 281 828 459 045.

Вкачестве простейшего приближения для числа e берут число 2,72 , т.е. с

точностью до 10 2 :

e 2,72 .

Здесь опустим доказательство того, что последовательность (3.14) строго возрастает и ограничена. Приведём простое доказательство только наличия у неё конечного предела.

Сначала докажем, что существует конечный предел у последова-

63

В соответствии с неравенством Бернулли (3.13)

yn .

Вравенстве (3.15) n стремится к бесконечности, принимая только натуральные значения. В дальнейшем это равенство будет обобщено (будет рассмотрена ситуация, когда аргумент стремится к бесконечности произвольным образом). В частности, имеет место следующее утверждение:

Равенство (3.16) и теорема 10 широко используются при вычислении пределов степенно-показательных выражений. Поясним это несколькими примерами.

Пример 1. Требуется вычислить

65

следующее:

Отметим, что число Эйлера выгодно применять в качестве основания для логарифмов. Логарифмы с основанием e называют натуральными.

3.11. Некоторые приложения понятия предела

этого факта внесено в упражнения).

Теперь поставим задачу о вычислении суммы геометрической прогрессии с первым членом a и знаменателем q при условии, что q 1.

Эта последовательность задаётся общим членом xn aqn 1 (см. гл. 2).

Так как имеется бесконечное число слагаемых, то сумму S ещё надо определить.

Получим сначала формулу для вычисления суммы первых n членов этой геометрической прогрессии. Нас интересует сумма

Sn a aq aq2 ... aqn 1, (3.17)

которую принято называть n -й частичной суммой. Умножим равенство (3.17) на q и полученное равенство Snq aq aq2 ... aq1 вычтем из

исходного. В результате получим равенство Sn qSn a aqn (часть членов при вычитании сократилась), откуда получаем искомую формулу для Sn :

Часто равенство (3.18) называют формулой для вычисления суммы конечной геометрической прогрессии.

Под суммой бесконечной геометрической прогрессии естественно понимать предел, к которому стремится сумма (3.17) при безграничном возрастании n . Отметим, что сумма (3.17) сама представляет собой после-

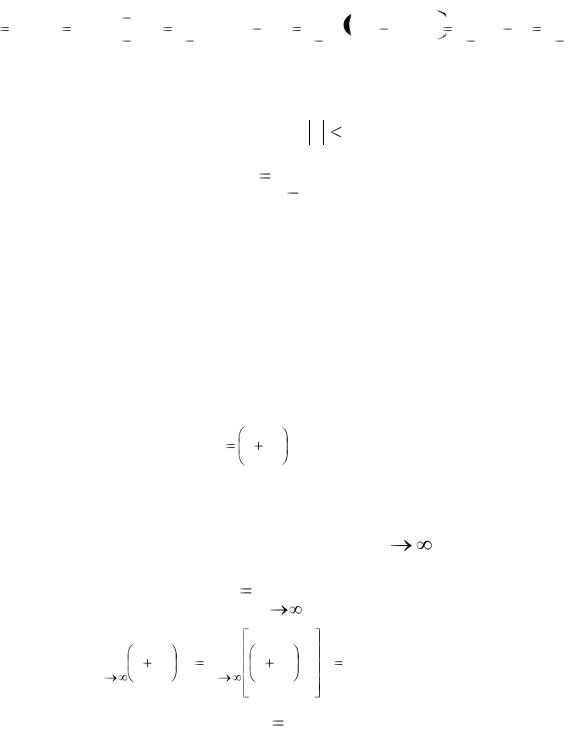
довательность Sn . Таким образом, надо перейти к пределу в равенстве

(3.18):

(3.20)

Из её членов образуем частичную последовательность следующим образом: в качестве первого члена новой последовательности выберем

член исходной последовательности с номером n1, в качестве второго члена новой последовательности – член исходной с номером n2 n1, и т.д. В результате получим новую последовательность

им пределом число a , то и каждая подпоследовательность этой последовательности сходится и имеет своим пределом число a .

68

одному и тому же числу a ; к этому же пределу сходится и сама исходная последовательность xn .

Действительно, так как xn также является подпоследовательно-

стью, то она сходится и имеет пределом некоторое число a . Но тогда и любая другая подпоследовательность также сходится и имеет тот же предел a .

Замечание. В примере 1 рассмотрен случай, когда последователь-

прос: «из любой ли последовательности можно выбрать сходящуюся подпоследовательность?» Ответ на этот вопрос, вообще говоря, отрицатель-

ный. Например, из последовательности xn 2n нельзя выбрать схо-

дящуюся подпоследовательность. Заметим, что эта последовательность неограниченная. Если же последовательность будет ограниченной, то положительный ответ на вопрос даёт следующая теорема, которая играет важную роль во многих исследованиях.

Теорема 18 (Больцано-Вейерштрасса). Из любой ограниченной последовательности можно выделить сходящуюся к конечному пределу подпоследовательность.

держит бесконечное число членов последовательности и обозначим его [a1,b1]. Поделим отрезок [a1,b1] пополам точкой d1. Тогда по крайней мере один из отрезков [a1, d1] или [d1,b1]содержит бесконечное число

должая этот процесс до бесконечности, получим последовательность вложенных отрезков

Согласно теореме 17 о вложенных стягивающихся отрезках существует единственная точка c принадлежащая всем отрезкам, к тому же

[ak , bk ] по одному члену из последовательности xn , который обозначим xnk . Это всегда можно сделать, так как любой из отрезков [ak , bk ] со-

держит бесконечное число элементов последовательности xn . При этом

применяя теорему 14 о промежуточной последовательности заключаем, что

3.13. Критерий Коши

Теорему Больцано-Вейерштрасса далее будем применять при доказательстве критерия Коши сходимости числовой последовательности. Этот критерий указывает внутренний свойства последовательности, обеспечивающие её сходимость или расходимость. Ценность критерия Коши заключается ещё и в том, что в отличие от введённого ранее определения сходимости числовой последовательности, не требуется знание численного значения её предела.

конечный предел, необходимо и достаточно, чтобы она была фундамен-

70

тальной.

Доказательство (необходимость). Пусть последовательность (3.20)