
5672
.pdf
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Хабаровская государственная академия экономики и права»
Кафедра математики и математических методов в экономике
П. Я. Бушин
Эконометрика
Корреляционно-регрессионный анализ
Хабаровск 2014
1
УДК 519.95
ББК В 1
Б 94
Бушин П. Я. Эконометрика. Корреляционно-регрессионный анализ. : учеб. пособие / П. Я. Бушин. – Хабаровск : РИЦ ХГАЭП, 2014. – 84 с.
Содержание учебного пособия в основном соответствует требованиям государственных образовательных стандартов высшего профессионального образования по направлению подготовки «Экономика» квалификации (степень) «бакалавр» очной формы обучения и программе дисциплины «Эконометрика».
В учебном пособии изложены теоретические положения корреляционнорегрессионного анализа – важнейшего раздела курса эконометрики. Приведены разнообразные методы анализа корреляций и регрессий как одномерных, так и многомерных, как непрерывных, так и дискретных переменных, приведены методы диагностики адекватности регрессионных моделей с помощью различных статистических тестов.
В пособии уделено достаточное внимание как традиционным методам анализа корреляций и регрессий, так и современным, таким, как тестирование ошибки спецификации уравнения регрессии и коррекции стандартных ошибок оценок в форме Уайта и Ньюи – Веста.
Каждый раздел пособия сопровождается рассмотрением практических примеров из экономики. В процессе их рассмотрения используются различные пакеты программ эконометрического анализа
Пособие предназначено для обучающихся по направлению «Экономика», кроме того, оно может быть использовано и магистрантами разных направлений обучения и специалистами, принимающими участие в выработке управленческих решений на основе корреляционно-регрессионного анализа.
Рецензенты:
Р. В. Намм, доктор физ.-мат. наук, профессор, гл. научный сотрудник ВЦ ДВО РАН
В. А. Кузнецов, канд. физ.-мат. наук, доцент кафедры ММиИТ ДВИ-филиал РАНХиГС
Утверждено издательско-библиотечным советом академии в качестве учебного пособия
 Бушин П. Я., 2014
Бушин П. Я., 2014  Хабаровская государственная академия экономики и права, 2014
Хабаровская государственная академия экономики и права, 2014
2
Введение
Эконометрика входит в число базовых дисциплин современного экономического образования. Как считает Самуэльсон, «эконометрика позволяет проводить количественный анализ реальных экономических явлений, основываясь на современном развитии теории и наблюдениях, связанных с методами получения выводов».
Данное учебное пособие предназначено для студентов экономического профиля и призвано кратко описать основные моменты эконометрического анализа, касающегося корреляционных и регрессионных зависимостей. В нём кратко рассмотрены простая и множественная корреляция и регрессия с изложением основных моментов эконометрической теории.
Автором рассмотрены классические модели корреляционно-регрессионного анализа, основные предпосылки метода наименьших квадратов, их тестирование и методы коррекции в случае их невыполнения на основе современных эконометрических методов.
Кроме того, в пособии рассмотрен случай использования дискретных зависимых и независимых переменных в регрессионном анализе, в том числе и на основе логистической регрессии.
Рассмотрены также вопросы оценки системы одновременных эконометрических уравнений на основе двухшагового метода наименьших квадратов с описанием процедуры их оценивания с помощью объекта «Sistem» эконометрического пакета программ EViews.
Изложение материала эконометрического анализа в пособии носит в основном прикладной характер, поэтому все рассмотренные в пособии темы сопровождаются иллюстрацией практических примеров, взятых из современной эконометрической литературы. Расчёты приведены в основном на эконометрическом пакете программ EViews и сопровождены описанием применяемых процедур и подробным экономическим анализом.
Несмотря на краткость рассмотрения эконометрических методов, данное пособие может служить справочником по применению этих методов для магистрантов и специалистов, использующих их в своих научных исследованиях.
Измерения в экономике
Слово «эконометрика» можно истолковать как измерения в экономике. Но прежде, чем что-то измерять, необходимо ввести меру или метрику. В эконометрике обычно измеряют информацию. Вводимая мера зависит от типа измеряемой информации. Общепринято считать, что существует четыре шкалы
3
измерения экономической информации – номинальная, ранговая, интервальная
ишкала отношений. Существуют и другие подходы к подобной классификации, но мы будем придерживаться этой общепринятой. Кроме того, есть разночтения
ив названиях шкал. Так, номинальную шкалу ещё называют шкалой наименований или категориальной шкалой, а ранговую шкалу – порядковой или ординальной шкалой.
Первые две шкалы измеряют так называемую качественную информацию. Это просто метки, которыми могут быть буквы, слова и числа, но числа здесь – это тоже метки. Например, в номинальной шкале объектами могут быть обозначения названий улиц города, имён или пола опрашиваемых индивидуумов, а в ранговой – предпочтения в каких-либо товарах или уровни квалификации работников фирмы и т. д.
Измерением в номинальной шкале можно считать любую классификацию, по которой класс получает числовое наименование (например, номер учебной специальности).
Шкала, в которой порядок элементов по уровню проявления некоторого свойства существенен, а количественное выражение различия несущественно, называется порядковой или ранговой. В этом случае кроме классификации возможно ещё и сравнение.
Понятно, что в этих двух случаях арифметические действия над данными объектами бессмысленны, но их можно сравнивать между собой и классифицировать в группы однородных объектов.
Кроме номинальной и порядковой шкал в экономических исследованиях используются интервальные шкалы. Измерения в этих шкалах в определённом смысле более совершенны. Здесь появляется возможность указать не только класс, к которому относится данный объект, но и описать его отличие от других объектов, рассчитав разность (интервал) между соответствующими позициями на шкале. В интервальной шкале не указывается абсолютный нуль, т. е. нуль не означает отсутствия признака, например в шкале температур. В этой шкале можно указать «на сколько» один показатель отличается от другого, но не «во сколько раз».
Примерами интервальных шкал могут служить измерения большинства экономических показателей (производительность труда, себестоимость, рентабельность, ликвидность и т. д.)
Вслучаях, когда на шкале можно указать абсолютный нуль, имеем более высокий уровень измерения, а именно – шкалу отношений. При измерении на такой шкале мы можем сказать не только, насколько один показатель отличается от другого, но и во сколько раз. По шкале отношений можно оценить такие социально-экономические характеристики, как стаж, заработная плата, прибыль
ит. д. Нуль на этой шкале означает отсутствие признака.
4

Итак, если в шкале отношений «работают» все четыре арифметических действия, то в интервальной шкале – только сложение и вычитание.
Кроме классификации информации по типам шкал различают также перекрёстные (пространственные) данные и временные ряды. В первом случае имеют дело с информацией, собранной для одного такта времени по нескольким объектам, охарактеризованным по нескольким признакам (например, работники фирмы, охарактеризованные по их профессиональным качествам). В случае же временных рядов имеем информацию по одному показателю в течение нескольких периодов времени (например, зарплата работника фирмы за год по неделям).
При работе с пространственной информацией, как правило, имеют дело со случайной выборкой, взятой из генеральной совокупности, поэтому здесь возможно применение теории оценивания, разработанной в курсе математической статистики.
В дальнейшем числовые характеристики генеральной совокупности будем называть параметрами, а их аналоги, вычисленные на основе выборки – выборочными характеристиками.
Основное свойство выборки – это её случайность, поэтому все выборочные характеристики – случайные числа, подчиняющиеся тому или иному закону распределения.
Не будем останавливаться здесь специально на теории оценивания, а если в эконометрическом анализе из этой теории понадобятся какие-то сведения, то они будут кратко приведены в соответствующем месте.
Глава 1. Простой корреляционный и регрессионный анализ
1.1.Коэффициент парной корреляции
Корреляционным анализом называется совокупность статистических приемов, с помощью которых исследуются и обобщаются взаимосвязи корреляционно связанных величин.
В эконометрике корреляционный анализ применяется для выявления наличия или отсутствия зависимостей между анализируемыми признаками. И только после утвердительного ответа на этот вопрос имеет смысл определять вид зависимости. В дальнейшем в основном будем иметь дело со случайными величинами, следующими нормальному закону распределения, поэтому, если не будет особо оговорено, будем говорить о линейной зависимости.
Меру линейной зависимости между величинами Y и X определяют с помощью ковариации. Она определяется как
= cov(Y,X) = M{(Y-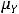 )(X-
)(X-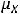 )},
)},
5
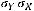
где 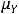 и
и 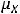 – соответственно, математические ожидания Y и X. Таким образом, ковариация между случайными переменными – это математическое ожидание произведения отклонений значений случайных переменных от их математических ожиданий. Если X = Y, то имеем дисперсию случайной величины X, т. е.
– соответственно, математические ожидания Y и X. Таким образом, ковариация между случайными переменными – это математическое ожидание произведения отклонений значений случайных переменных от их математических ожиданий. Если X = Y, то имеем дисперсию случайной величины X, т. е.
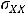 =
= 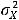 = M{(X-
= M{(X-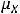 )2}.
)2}.
Корень квадратный из дисперсии называется стандартным отклонением и обозначается как  . Если известно, о какой переменной идёт речь, то нижний индекс у стандартного отклонения и дисперсии обычно не ставится.
. Если известно, о какой переменной идёт речь, то нижний индекс у стандартного отклонения и дисперсии обычно не ставится.
Чем больше величина ковариации, тем теснее линейная связь между переменными. Но с этой характеристикой не совсем удобно работать, т. к. её величина зависит от единиц измерения анализируемых показателей. Чтобы избавиться от этого недостатка, ковариацию стандартизируют двумя стандартными отклонениям, получая при этом коэффициент корреляции, т. е.
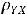 =
= 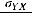 .
.
Коэффициент корреляции всегда лежит между –1 и +1 и не зависит от масштаба переменных. Если ковариация cov(Y,X) = 0, то говорят, что случайные переменные некоррелированны, т. е. между ними отсутствует линейная зависимость. То же самое можно говорить и о коэффициенте корреляции. Если случайные величины статистически независимы, то 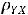 = 0, а в случае нормального распределения из их некоррелированности, когда
= 0, а в случае нормального распределения из их некоррелированности, когда 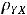 = 0, следует их независимость. Две случайные переменные Y и X коррелированы полностью (
= 0, следует их независимость. Две случайные переменные Y и X коррелированы полностью (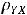 = 1), если Y = aX для некоторого положительного значения a.
= 1), если Y = aX для некоторого положительного значения a.
Далее будем пользоваться свойствами дисперсии и ковариации, из которых следует, что дисперсия суммы двух некоррелированных переменных равна сумме дисперсий этих переменных, а ковариация двух переменных равна математическому ожиданию произведения этих переменных, если математическое ожидание хотя бы одной из них равно нулю.
Покажем последнее. Пусть 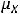 = 0. Тогда cov(Y,X) = M{(Y –
= 0. Тогда cov(Y,X) = M{(Y – 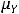 )(X –
)(X –  )} = =M{(Y –
)} = =M{(Y – 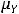 )(X)} = M{(YX) –
)(X)} = M{(YX) – 
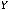 X)} = M{(YX) – M
X)} = M{(YX) – M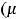
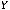 X)} = M{(YX) –
X)} = M{(YX) – 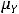
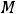 (X)}= = M{(YX)}–
(X)}= = M{(YX)}– 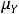
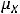 = M{(YX)}. Т. е. в нашем случае cov(Y,X) = M{(YX)}.
= M{(YX)}. Т. е. в нашем случае cov(Y,X) = M{(YX)}.
До сих пор рассуждения велись по отношению к параметрам генеральной совокупности. Исследователь обычно работает с выборками, на основе которых получает приближённые значения параметров. Эти приближённые значения называют оценками параметров. Для того чтобы оценки были «хорошими», необходимо, чтобы они были несмещёнными, эффективными и состоятельными.
Оценка называется несмещённой, если её математическое ожидание равно самому оцениваемому параметру. Несмещённость оценки означает, что она в среднем соответствует оцениваемому параметру.
6

Оценка называется эффективной, если она обладает наименьшей дисперсией среди всех альтернативных оценок.
Оценка называется состоятельной, если при увеличении объёма выборки оценка сходится к оцениваемому параметру.
Так, известно, что выборочная средняя арифметическая является несмещённой оценкой генеральной средней. В дальнейшем оценку параметра будем обозначать той же буквой, что и параметр, но сверху будем помечать её знаком «крышки». Тогда можно записать, что 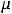 =
= 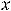 , где
, где 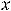 – выборочная средняя арифметическая. А выборочная дисперсия – смещённая оценка генеральной дисперсии и первую приходится подправлять, вводя поправочный коэффициент. Так, если выборочную дисперсию обозначить через S2, то несмещённой оценкой генеральной дисперсии будет
– выборочная средняя арифметическая. А выборочная дисперсия – смещённая оценка генеральной дисперсии и первую приходится подправлять, вводя поправочный коэффициент. Так, если выборочную дисперсию обозначить через S2, то несмещённой оценкой генеральной дисперсии будет 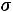 2 =
2 = 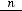 S2.
S2.
Оценкой коэффициента корреляции генеральной совокупности является выборочный коэффициент корреляции, определяемый из соотношения
=  =
= 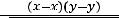 =
= 

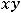
где в числителе стоит выборочная ковариация, а в знаменателе – произведение выборочных стандартных отклонений.
Поскольку речь здесь идёт об оценке, а оценка – величина случайная, то необходимо проверить её надёжность. Осуществляется это с помощью проверки гипотезы о том, что коэффициент корреляции генеральной совокупности равен нулю. Итак, нулевая гипотеза H0 : 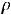 = 0, альтернативная Ha :
= 0, альтернативная Ha : 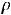
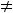 0.
0.
Проверяются статистические гипотезы по стандартному алгоритму. Сначала по выборочным данным вычисляется статистика, закон распределения которой известен, если верна нулевая гипотеза. Затем по фиксированному уровню значимости и известному числу степеней свободы определяются критические точки данного распределения. По критическим точкам определяется область принятия гипотезы и критическая область. Если вычисленное значение статистики попало в область принятия гипотезы, то нулевая гипотеза не отклоняется. В противном случае – отклоняется.
В нашем случае рассчитывается t-статистика вида
t = |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|||||||
|
|
|
|
|
|
|
|
||
Известно, что если верна нулевая |
гипотеза, т. е. если |
= 0, то эта |
|||||||
статистика следует распределению Стьюдента с (n–2) степенями свободы.
Зафиксировав уровень |
значимости |
(обычно его принимают равным 0,05), |
|
определяем |
критические точки ( |
) и по ним строим область принятия |
|
гипотезы: (– |
;+ |
Если вычисленное значение t-статистики попало в эту |
|
|
|
|
7 |

область, то говорят, что коэффициент корреляции незначимо отличен от нуля и линейная зависимость между анализируемыми переменными отклоняется. Критические точки обычно определяются по таблице критических значений распределения Стьюдента.
При компьютерных расчётах обычно вычисляется расчётный уровень значимости (их в статистических пакетах обозначают по-разному: p-value, p- level, sign, Prob. и т. д.), это вероятность того что 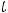
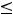
 . Т. е. p-value = P(
. Т. е. p-value = P( 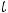
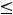
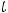 ). Грубо говоря, это вероятность того, что вычисленное значение t-статистика попало в область принятия гипотезы. Расчётный уровень значимости сравнивают с принятым уровнем значимости (у нас это
). Грубо говоря, это вероятность того, что вычисленное значение t-статистика попало в область принятия гипотезы. Расчётный уровень значимости сравнивают с принятым уровнем значимости (у нас это 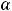 ) и, если p-value
) и, если p-value 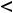
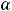 , то H0 отклоняется и считается, что переменные x и y коррелированы, Если p-
, то H0 отклоняется и считается, что переменные x и y коррелированы, Если p-
value |
, то H0 не отклоняется и считается, что переменные не коррелированы. |
||
Если расчётный уровень значимости близок к |
, то при принятии |
||
решения рекомендуется проверять, выполняется ли неравенство |
. |
||
Для качественной интерпретации значений коэффициентов парной линейной корреляции (в случае их значимого отличия от нуля) можно использовать шкалу Чеддока:
Величина коэфф. |
0,1 – 0,3 |
0,3 – 0,5 |
0,5 – 0,7 |
0,7 – 0,9 |
0,9 – 0,99 |
|
|
|
|
|
|
Характеристика |
слабая |
Уме- |
заметная |
высокая |
весьма |
силы связи |
|
ренная |
|
|
высокая |
|
|
|
|
|
|
1.2. Парная (простая) линейная регрессия
После того как с помощью корреляционного анализа выявлено наличие статистически значимых связей между переменными и оценена степень их тесноты, обычно переходят к математическому описанию конкретного вида зависимостей с помощью регрессионного анализа.
Корреляционная зависимость между двумя переменными – это функциональная зависимость между одной переменной и ожидаемым (условным средним) значением другой. Уравнение такой зависимости между двумя переменными называется уравнением регрессии. В случае, если переменных две (одна зависимая и одна независимая), то регрессия называется простой, а если их более двух, то множественная. Если зависимость между переменными линейная, то регрессия называется линейной, в противном случае – нелинейной.
Рассмотрим подробно простую линейную регрессию. Модель такой зависимости может быть представлена в виде
y = α + βx + ε, (1.1)
где у – зависимая переменная (результативный признак);
8

х – независимая переменная (факторный признак); α – свободный член уравнения регрессии или константа;
β– коэффициент уравнения регрессии;
ε– случайная величина, характеризующая отклонения фактических значений зависимой переменной у от модельных или теоретических значений, рассчитанных по уравнению регрессии.
При этом предполагается, что объясняющая переменная х – величина не случайная, а объясняемая y – случайная. В дальнейшем это предположение можно будет убрать.
1.2.1.Метод наименьших квадратов (МНК) и его предпосылки
αи β – это параметры модели регрессии (1.1), которые должны быть оценены на основе выборочных данных. На основе этих же выборочных данных должна быть оценена дисперсия ε. Одним из методов вычисления таких оценок является классический метод наименьших квадратов (МНК). Суть МНК состоит в минимизации суммы квадратов отклонений фактических значений зависимой
переменной у от их условных математических ожиданий |
~ |
, определяемых по |
||||||||
y |
||||||||||
уравнению регрессии: |
~ |
= α |
+ βx, |
в |
предположении, |
что математическое |
||||
y |
||||||||||
|
|
|
|
|
|
|
|
|
|
~ |
ожидание ε равно нулю. Математическое ожидание y обозначим через y , а |
||||||||||
сумму квадратов отклонений через Q( |
|
|
. |
|
|
|
|
|||
Q( |
|
= |
( yi |
2 |
= ( yi ( |
xi )) |
2 |
. |
||
|
yi ) |
|
|
|||||||
|
|
|
i |
|
|
i |
|
|
|
|
Здесь суммирование ведётся по всей генеральной совокупности. Данную
сумму называют остаточной суммой квадратов. |
|
|
|
Чтобы минимизировать эту функцию по параметрам |
обратимся |
к |
|
условиям первого порядка, полученным дифференцированием |
Q( |
) |
по |

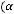
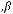
 = –2
= –2 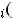
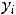

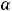

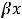
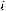 ),
),
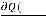
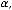
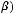 = –2
= –2 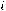
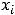
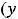
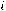

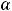

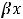
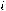 ).
).
Далее пусть для оценки параметров модели (1.1) организована выборка, содержащая n пар значений переменных (xi,yi), где i принимает значения от 1 до n (i=1, n ). Приравнивая частные производные к нулю и переходя от генеральной совокупности к выборке (заменив параметры на их оценки), получим систему нормальных уравнений для вычисления оценок параметров α и β. Обозначим эти оценки соответственно как а и b. Получим следующую систему нормальных уравнений
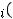
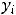

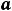

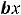
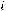 ) = 0,
) = 0, 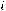

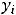

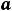

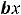
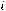 ) = 0.
) = 0.
9

Если оценённое уравнение обозначить как y = a + bx + e, где е – одна из реализаций случайной величины ε, соответствующая конкретной выборки, то выражение в скобках системы нормальных уравнений есть не что иное, как
остаток уравнения регрессии еi = yi |
|
|
|
и тогда первое уравнение этой |
|
|
|
||||
системы примет вид |
= 0. То есть среднее значение остатков равно нулю. |
||||
Таким образом, если уравнение регрессии содержит константу, то сумма остатков в оценённом уравнении всегда равна нулю.
Второе уравнение системы в этих обозначениях даёт |
= 0, т. е. векторы |
|||||||||||||
значений независимой переменной и остатков ортогональны (независимы). |
||||||||||||||
Приведём один из вариантов формул для вычисления таких оценок: |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = |
|
– b |
|
, b = |
xy |
x y |
. |
(1.2) |
||||||
y |
x |
|||||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
sx |
2 |
|
|
|
|
|
|
Известно также, что несмещённой оценкой дисперсии случайных отклонений является остаточная дисперсия, вычисляемая из соотношения:
|
|
|
|
2 |
|
S 2 |
= |
( y |
y) |
|
. |
|
|
|
|||
ост |
|
n |
2 |
|
|
|
|
|
|
Итак, оценённая модель линейной парной регрессии имеет вид
y = a + bx + e, |
(1.3) |
где е – наблюдаемые отклонения фактических значений зависимой переменной у
от расчётных |
|
, которые рассчитываются из соотношения |
|
= a + bx. |
y |
y |
Различие между ε и е состоит в том, что ε – это случайная величина и предсказать её значения не представляется возможным, в то время как е – это
наблюдаемые значения отклонений (е = у – ) и эти отклонения можно считать y
случайной выборкой из совокупности значений остатков регрессии и их можно анализировать с использованием статистических методов.
Как было отмечено, МНК строит оценки регрессии на основе минимизации суммы квадратов отклонений или остатков ε, поэтому важно знать их свойства. Для получения «хороших» МНК-оценок необходимо, чтобы выполнялись следующие основные предпосылки относительно остатков модели (1.1), называемые предположениями Гаусса – Маркова.
1.М(εi) = 0, (i = 1,…,n);
2.( ,…,
,…, 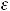

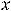 ) независимы;
) независимы;
3.D(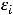 ) =
) = 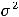 , (i = 1,…,n);
, (i = 1,…,n);
4.Cov(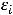
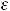 ) = 0, (i,j = 1,…,n), i
) = 0, (i,j = 1,…,n), i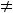
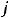 .
.
Первое предположение говорит о том, что математическое ожидание регрессионных остатков равно нулю и подразумевает, что в среднем, линия регрессии должна быть истинной. Предположение 3 утверждает, что все регрессионные остатки имеют одну и ту же дисперсию, и называется предположением гомоскедастичности, а предположение 4 исключает любую
10
