5672

Кроме того, этот показатель в неявном виде участвует в определении ещё одного показателя точности уравнения множественной регрессии, а именно – коэффициента множественной детерминации (R–squared или R2). Как известно,

R 2 1 SSR SST

или после преобразований (в случае, если в уравнении регрессии присутствует константа)

Отсюда следует, что коэффициент множественной детерминации показывает долю вариации зависимой переменной, обусловленную вариацией включённых в уравнение регрессии независимых переменных, или, иными словами, долю вариации зависимой переменной, обусловленную регрессионной зависимостью.

Коэффициент множественной детерминации изменяется от нуля до единицы и равен единице, если SSR = 0, (связь линейная, функциональная), и равен нулю, если SST = SSR, (линейная связь отсутствует).

Из определения коэффициента множественной детерминации следует, что он будет увеличиваться при добавлении в уравнение регрессии независимых переменных, как бы слабо не были они связаны с независимой переменной. Следуя этой логике, в уравнение регрессии для увеличения точности отражения изучаемой зависимости может быть включено неоправданно много независимых переменных. Точность уравнения при этом может увеличиться незначительно, а размерность модели возрасти так, что её анализ будет затруднён. Кроме того, при этом уменьшается число степеней свободы модели и ухудшается точность оценок. Для преодоления этого недостатка был разработан исправленный (на число степеней свободы) коэффициент (Adjusted R-squared), имеющий вид

или после преобразования

В отличие от R2 , Radj2 будет убывать, если в уравнение регрессии будут

добавляться незначимые независимые переменные (с t-статистикой < 1). Исправленный коэффициент позволяет избежать переоценки независимой

переменной при включении её в уравнение регрессии. Если добавление

31

переменной приводит к увеличению Radj2 , то включение её в уравнение

регрессии оправданно, в противном случае – нет.

Продолжим анализ точности уравнения регрессии. Как уже отмечалось, при проверке значимости уравнения регрессии проверяется гипотеза о том, что все коэффициенты модели регрессии равны нулю. Если нулевая гипотеза отклоняется, то это означает, что не все коэффициенты в модели регрессии равны нулю, и тогда встаёт вопрос о проверке значимости каждого параметра регрессии в отдельности.

Такая проверка осуществляется на основе t-статистик, определяемых из соотношений

Здесь [(XTX)-1]kk – соответствующие диагональные элементы матрицы (XTX)-1 . При компьютерных расчётах вместе с t-статистикой (t-Statistic) для каждой

оценки параметров уравнения регрессии вычисляется выборочный уровень значимости или Prob – это вероятность того, что вычисленное значение t-статистики не превосходит критического значения. По его значению и определяется значимость каждой оценки параметров уравнения регрессии.

2.2.4. Мультиколлинеарность

Одним из условий классической регрессионной модели является предположение о линейной независимости объясняющих переменных, что означает независимость столбцов матрицы регрессоров X. Это обеспечивает неравенство нулю определителя матрицы ХТХ и существование обратной матрицы (XTX)-1, которая используется в МНК при вычислении оценок параметров уравнения регрессии (TX)-1XTY). При нарушении этого условия говорят, что имеет место совершенная мультиколлинеарность и тогда нельзя построить МНК-оценку параметров модели.

На практике полная коллинеарность встречается редко, чаще приходится сталкиваться с ситуацией, когда анализируемые признаки тесно связаны друг с другом. Тогда говорят о наличии мультиколлинеарности. В этом случае МНК-оценка формально существует, но обладает «плохими» свойствами.

Объясняется это тем, что определитель матрицы (XTX) в этом случае близок к нулю, а при вычислении обратной матрицы элементы союзной матрицы делятся на этот определитель, в результате чего все элементы обратной матрицы будут не оправдано большими. А они используются при вычислении стандартных

32

большие по величине. В результате чего оценки рассчитываются с грубыми ошибками, что приводит к искажению смысла таких оценок (иногда даже по знаку). Кроме того, эти ошибки участвуют при вычислении t-статистик для

равенстве нулю коэффициентов регрессии.

Мультиколлинеарность может возникнуть в силу разных причин, например, при анализе временных рядов несколько независимых переменных могут иметь общий временной тренд или в качестве независимых переменных выступают лаговые значения одной и той же переменной и т. д.

Нет однозначного метода решения проблемы мультиколлинеарности. Иногда достаточно удалить какую-либо переменную из уравнения, но при этом не всегда ясно, какая из них «лишняя». А если эта переменная значимо влияет на зависимую переменную, то это влияние перейдёт на остатки и они могут стать коррелированными, к тому же это может вызвать смещение оценок.

2.2.5. Тестирование предпосылок МНК для множественной регрессии

Анализ остатков уравнения множественной регрессии на автокорреляцию

то говорят об автокорреляции остатков. Причин возникновения автокорреляции в остатках для уравнения множественной регрессии несколько. Выделим среди них следующие:

1)в регрессионную модель не введен значимый факторный признак и его изменение приводит к значимому изменению последовательных остаточных величин;

2)в регрессионную модель не включено несколько незначимых факторов, но их изменения совпадают по направлению и фазе, и их суммарное воздействие приводит к значимому изменению последовательных остатков:

3)неверно выбран вид зависимости между анализируемыми переменными;

4)автокорреляция остатков может возникнуть не в результате ошибок,

допущенных при построении регрессионной модели, а вследствие

33

особенностей внутренней структуры случайных компонент (например, при описании регрессией динамических рядов).

Анализ остатков на автокорреляцию, как и в случае парной регрессии, можно проводить на основе критерия Дарбина – Уотсона (Durbin – Watson test). Табличные значения этого критерия определяются при известных n (объём выборки), m (число независимых переменных) и α (принятый уровень значимости). Дальнейшие исследования – по аналогии с простой регрессией. Если с помощью этого критерия обнаружена существенная автокорреляция остатков, то необходимо признать наличие проблемы в определении спецификации уравнения и либо пересмотреть набор включаемых в уравнение регрессий переменных, либо форму регрессионной зависимости. В большей степени такой анализ актуален при рассмотрении регрессии на временные ряды.

Как уже отмечалось, статистика Дарбина – Уотсона обладает рядом недостатков и в некоторых случаях её использование проблематично: тестируется только автокорреляция первого порядка, нельзя использовать, если среди регрессоров есть лаговые значения зависимой переменной, необходимо присутствие в регрессии константы и т. д.

Поэтому разработаны альтернативные тесты для проверки автокорреляции в остаточных членах уравнения регрессии, лишённые таких недостатков.

Рассмотрим один из них реализованный в пакете EViews. Этот тест носит имя своих авторов – тест Бройша – Годфри (Breusch – Godfrey test). Идея этого теста в следующем. Сначала обычным МНК оценивается исходное уравнение регрессии. Затем составляется вспомогательное уравнение регрессии, в котором зависимой переменной являются остатки исходного уравнения, а независимыми – константа, исходные независимые переменные и лаговые значения остатков исходного уравнения. Число лаговых значений остатков во вспомогательном уравнении определяется эмпирически. Затем оценивается вспомогательное уравнение и рассчитывается статистика nR2 , где n – объём выборки, а R 2 – коэффициент множественной детерминации вспомогательного уравнения. Доказано, что если автокорреляция в остатках исходного уравнения отсутствует, то статистика nR2 следует распределению (хи-квадрат распределению с p степенями свободы), где p – максимальное число лаговых значений остатков во вспомогательном уравнении. Если окажется, что nR2 >

2 , то гипотеза об отсутствии автокорреляции в остатках отклоняется.

крит.

Опишем этот тест на примере уравнения регрессии с двумя переменными. Пусть рассматривается следующее исходное уравнение:

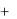yt 0 t .

Чтобы протестировать остаточные члены этого уравнения на автокорреляцию (на серийную корреляцию) по тесту Бройша – Годфри, оценим исходное уравнение стандартным МНК и составим вспомогательное уравнение

34

вывод на основе расчётного уровня значимости. В EViews этот тест называется serial correlation LM test – тест максимального правдоподобия на последовательную корреляцию. Реализуется этот тест выбором процедуры

«View/Residual Tests/serial correlation LM test». В диалоговом окне теста будет предложено выбрать максимальный порядок лага (по умолчанию проставлен 2). Выбор величины лага зависит от того, какой максимальный порядок автокорреляции в остатках необходимо проверить.

Отметим ещё раз, что тестирование остатков регрессии на автокорреляцию в основном рекомендуется, если анализируются временные ряды. При анализе пространственной информации изучаются в основном случайные выборки, и понятие порядка автокорреляции теряет смысл.

Тестирование остатков на гомоскедастичность

Как уже отмечалось, одной из важных предпосылок МНК является предпосылка о гомоскедастичности остатков, т. е. о постоянстве дисперсии остаточных членов уравнения регрессии. Выполнение этой предпосылки (наряду с другими) обеспечивает хорошие качества МНК-оценок.

Последствия невыполнения этой предпосылки схожи с аналогичными при наличии автокорреляции в остатках (неэффективность оценок и смещённость их ошибок). В результате этого статистические выводы на основе полученных оценок могут быть ошибочными и привести к неверным заключениям по построенной модели.

Гетероскедастичность встречается как при анализе пространственной информации, особенно, когда анализируются абсолютные показатели, отражающие масштаб изучаемого явления или процесса (доходы, прибыль, зарплата и т. д.), так и временных рядов, если их уровни растут с течением времени.

Разработаны различные методы по выявлению гетероскедастичности остатков. Так, выше был рассмотрен критерий Голдфелда – Квандта (Goldfeld – Quandt test), но он «работает» только в случае, если остатки пропорциональны значениям независимой переменной. А если переменных несколько, то не совсем понятно, по какой из них надо производить упорядочение.

Рассмотрим один из альтернативных методов, реализованном в EViews. Это тест Уайта (White test) на гетероскедастичность.

35

Идея этого теста в следующем. Оценивается исходное уравнение регрессии и затем строится вспомогательное уравнение зависимости квадрата остатков исходного уравнения от всех независимых переменных, их квадратов и

При этом проверяется нулевая гипотеза о том, что не существует связи между дисперсией остатков исходного уравнения и независимыми переменными, т. е. остатки et гомоскедастичны. Доказано, что если верна

нулевая гипотеза, то nR2 следует распределению 2 ( p) (хи-квадрат распределению с p степенями свободы), где n – объём выборки, R 2 – коэффициент множественно детерминации вспомогательного уравнения, p – число регрессоров во вспомогательном уравнении (без константы).

В этом случае Probability для Obs*R-squared будет больше принятого уровня значимости .

Для проведения теста Уайта (после оценки уравнения регрессии) в EViews

нужно выбрать «View/Residual Test/ White Heteroskedasticity (cross term)».

Тестирование остатков на нормальный закон распределения

Тестов на нормальный закон распределения разработано достаточно много. У каждого из них есть свои преимущества и недостатки. Остановимся здесь на одном из них, реализованном в эконометрическом пакете EViews. Этот тест носит название своих авторов (Jarque – Bera test).

Статистика Jarque – Bera (JB) (Харке – Бера) предназначена для проверки нулевой гипотезы о нормальном законе распределения для значений рассматриваемой переменной. Статистика (JB) в EViews рассчитывается из соотношения

где S – асимметрия; К – эксцесс; n – объём выборки; k – число оцениваемых параметров в регрессии. Известно, что для нормального закона распределения S = 0, К = 3, тогда и JB = 0. JB-статистика в предположении верности нулевой

гипотеза о нормальном законе распределения отклоняется (при этом Probability для JB будет меньше ).

Отметим ещё раз, что критерии Дарбина – Уотсона и Голдфелда – Квандта являются точными (неасимптотическими) в том смысле, что они непосредственно учитывают количество наблюдений в выборке. В противоположность этому критерии Харке – Бера, Бройша – Годфри и Уайта являются асимптотическими и хорошо приближаются распределением хиквадрат только при большом объёме наблюдений. Поэтому вполне полагаться на результаты применения последних можно только при больших объёмах выборки..

Тестирование ошибки спецификации уравнения регрессии

Как уже отмечалось, среди предпосылок МНК присутствует предпосылка о нулевом математическом ожидании остатков регрессионной модели и, если при этом остатки и регрессоры независимы, оценки параметров уравнения регрессии будут несмещёнными. Тестирование предположения о том, что в рамках нормальной линейной модели M() = 0, (i = 1,2,…,n) осуществляется на основе критерия Рэмси RESET ( s Regression Equation Specification Error Test).

При помощи этого критерия можно выявить:

•наличие пропущенных переменных (т.е. невключение в правую часть уравнения некоторых существенных переменных);

•неправильную функциональную форму представления переменных (например, использование логарифмов переменных вместо их уровней);

•наличие корреляции между объясняющими переменными и остатками уравнения регрессии.

Рассмотрим идею этого теста, реализованного в пакете EViews. В этом тесте сначала оценивается исходная модель и по ней находятся расчётные значения

зависимой переменной , (i=1,…,n).

Затем оценивается вспомогательная модель, в которую помимо исходных

Эту гипотезу можно тестировать с помощью обычного F-теста. Обычно этот тест применяется при небольших значениях r =1,2,3.

Идея этого теста заключается в том, что добавлением нелинейных членов в уравнение регрессии не удаётся улучшить его качество.

37

2.2.6. Учёт некоторых нарушений стандартных предположений о модели

Рассмотрим кратко один из вариантов решения проблем, возникающих при наличии автокорреляции и гетероскедастичности в остатках регрессионных уравнений. Как уже отмечалось, в этих случаях МНК-оценки параметров уравнений регрессии будут состоятельными и несмещёнными, но несостоятельными и смещёнными могут оказаться ошибки этих оценок. В связи с этим одним из методов коррекции статистических выводов состоит в использовании обычных МНК-оценок, со скорректированными стандартными ошибками этих оценок, с учётом их автокорреляции и гетероскедастичности .

Рассмотрим эти два случая по отдельности. Предположим, что после оценивания параметров модели каким-либо методом было выяснено, что имеет место гетероскедастичность остатков этой модели при отсутствии какой-либо автокорреляции. Поскольку сами оценки при этом будут несмещёнными, то для верных статистических выводов достаточно будет скорректировать стандартные ошибки этих оценок. Одним из вариантов получения скорректированных на гетероскедастичность стандартных ошибок был предложен Уайтом и реализован в ряде пакетов анализа статистических данных, в том числе и в EViews. При этом удовлетворительные свойства скорректированной оценки Уайта (White estimator или White standard errors) гарантируются только при большом количестве наблюдений.

Оценка Уайта строится на основе явного выражения для ковариационной матрицы вектора оценок коэффициентов линейной эконометрической модели, в которой ошибки хотя и имеют нулевые математические ожидания, но не являются одинаково распределёнными, т. е. с разными дисперсиями, но взаимно независимы. Тогда ковариационная матрица остатков примет вид Cov() = diag(), т. е. на главной диагонали проставлены дисперсии остатков (для каждого остатка своя дисперсия), а вне диагонали – нули (какая-либо автокорреляция отсутствует). Для оценки этих n дисперсий имеется всего n наблюдений. Тем не менее можно получить состоятельную оценку этой ковариационной матрицы, заменив неизвестные дисперсии ошибок, на квадраты остатков, полученных в результате оценки модели обычным МНК. Это приводит к оценке Уайта.

Понятно, что это не единственный вариант корректировки последствий гетероскедастичности остатков уравнения регрессии. Иногда достаточно изменить вид зависимости или преобразовать переменные (например, перейти к логарифмам объясняемых переменных вместо их исходных значений).

Пусть теперь имеем более сложный случай, когда остатки не только гетероскедастичны, но и автокоррелированы. Поскольку последствия

38

автокорреляции в остатках аналогичны уже рассмотренным в случае их гетероскедастичности, можно воспользоваться аналогичной процедурой коррекции статистических выводов и при автокоррелированных остатках.

Один из вариантов получения скорректированных на автокоррелированность и гетероскедастичность значений был предложен Ньюи и Вестом (Newey,West) и реализован, например, в EViews, при этом удовлетворительные свойства оценки Ньюи – Веста (Newey – West estimate или Newey – West standard errors) как и в предыдущем случае гарантируются при большом количестве наблюдений. От предыдущего случая этот вариант поведения остатков отличается ещё и тем, что ковариационная матрица остатков не является диагональной (предполагается автокорреляция остатков, причём не обязательно только первого порядка), но и в этом случае авторам удалось получить состоятельную оценку указанной ковариационной матрицы.

Следует отметить, что автокореляция в остатках может появиться и потому, что при выборе объясняющих переменных была пропущена значимая переменная, и её влияние на зависимую переменную будет отражаться на поведении остатков. Кроме того, автокорреляция в остатках может появиться и при не правильном выборе вида зависимости. Ясно, что в этих случаях простой коррекцией ошибок оценок не обойтись. Необходимо провести более тщательный анализ при определении спецификации уравнения регрессии. Подобные ошибки в спецификации уравнения регрессии вряд ли удастся нейтрализовать описанными методами.

Пример 2. Тестирование предпосылок МНК Проиллюстрируем вышеизложенные положения на условном примере, в

котором описывается зависимость пятилетних процентных ставок (r60) от одномесячных (r1), квартальных (r3) , полугодовых (r6) и годовых (r12) процентных ставок (данные взяты из М. Вербик, 2008). На рисунке 2.6 приведены графики этих переменных.

39

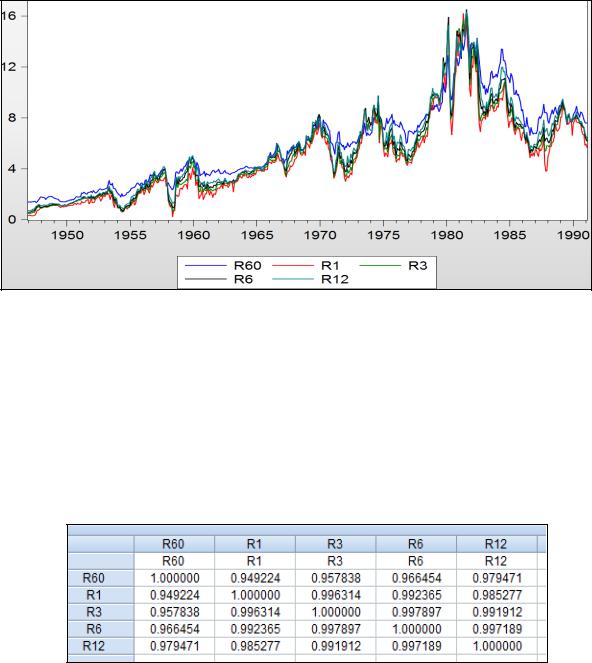
Рисунок 2.6 – Графики динамики анализируемых переменных

На рисунке 2.6 видим, что анализируемые переменные изменяются во времени почти параллельно, что может быть причиной их коллинеарности, в чём действительно убеждаемся, просмотрев матрицу парных коэффициентов корреляции (рисунок 2.7). Все коэффициенты корреляции между независимыми переменными оказались больше 0,9. В этом случае «доверять» коэффициентам уравнения не рекомендуется.

Рисунок 2.7. – Матрица парных коэффициентов корреляции

40