Рисунок 1.3 – Графики остатков, выборочных и расчётных значений для расходов

Гомоскедастичность остатков проверим тестом Голдфелда – Квандта. Для этого всю выборку разобьём на три части по 20 наблюдений, рассчитаем уравнения регрессии поотдельности для первых 20 наблюдений и для последних 20 наблюдений и выпишем остаточные суммы квадратов этих уравнений (Sum squared resid). Получим для первой части выборки 1 246,276, а для третьей – 4 164,0 (рисунок 1.4 и рисунок 1.5). Обратите внимание на позицию Sample – выборка. В первом случае в окне спецификации было установлено «1 20» (т. е. первых 20 наблюдений), а во втором – «41 60» (последних 20 наблюдений).

Рисунок 1.4 – Регрессия для первых 20 наблюдений

21

Рисунок 1.5 – Регрессия для последних 20 наблюдений

Вычислим F-статистику как отношение этих двух дисперсий и сравним с

критическим значением. Получим F = 3,34, а табличное значение F(20;20;0,05) = 2,1. Поскольку выборочное значение F-статистики оказалось больше табличного, то гипотеза о равенстве дисперсий отклоняется, и делаем вывод, что дисперсии различаются значимо, а значит, остатки анализируемого уравнения гетероскедастичны (растут с ростом доходов).

Тестирование предпосылки о нормальном законе распределения остатков проведём тестом Jarque – Bera, который сравнивает асимметрию и эксцесс остатков с асимметрией и эксцессом нормального закона распределения.

Чтобы провести это тестирование, необходимо после оценки уравнения регрессии сначала создать остатки, выбрав Proc/Make Residual Series…/OK.

Затем выбрать View/Descriptive Statistics&Tests/Histogram and Stats. Получим рисунок 1.6. Здесь кроме гистограммы остатков приведены описательные статистики остатков, а также асимметрия (Skewness) и эксцесс (Kurtosis). Известно, что для нормального закона распределения эти характеристики равны соответственно 0 и 3. Статистика Jarque – Bera рассчитывается из соотношения

JB = (n–k) ,

где n – объём выборки, k – число оцениваемых параметров, S – асимметрия, K – эксцесс. Поскольку в нашем случае вероятность больше 0,05, то гипотезе о нормальном законе распределения остатков не отклоняется.

22

Рисунок 1.6 – Гистограмма остатков и тест Jarque – Bera

Как поступить, если установлены наличие автокорреляции и гетероскедастичность остатков, а также тестирование второй предпосылки МНК

– рассмотрим далее, при анализе уравнения множественной регрессии.

Глава 2. Множественная корреляция и регрессия

Простая регрессия редко используется в практических исследованиях, т. к. экономические явления, как правило, определяются несколькими одновременно и совокупно действующими факторами. В связи с этим возникает задача исследования зависимости одной зависимой переменной от нескольких независимых переменных. В этом случае мы имеем дело с множественным регрессионным анализом, который сочетается с множественным корреляционным анализом.

Одно из различий этих двух видов анализа заключается в том, что в корреляционном анализе переменные равноправны, а в регрессионном анализе они делятся на зависимые и независимые. Такое деление в последнем случае хотя и обязательно, но довольно условно. Причинно-следственные связи устанавливаются обычно вне статистических методов исходя из профессионально-логических соображений. Статистические же методы позволяют изучать лишь зависимости между переменными.

Корреляционный анализ обычно предшествует регрессионному анализу, поэтому рассмотрим сначала его.

23

2.1. Множественный корреляционный анализ

2.1.1. Анализ матрицы парных коэффициентов корреляции

Такая матрица состоит из коэффициентов парных корреляций, рассчитанных для набора переменных y, x1, x2,….., xm и размещённых в виде матрицы. В дальнейшем переменную y будем называть зависимой, а остальные – независимыми. Для корреляционного анализа эти переменные равноправны, но для удобства анализа мы их будем различать.

Поскольку rxy = ryx, то корреляционная матрица симметрична относительно главной диагонали, поэтому естественно анализировать только одну из её частей (верхнюю или нижнюю относительно главной диагонали). Пусть

Задача анализа такой матрицы обычно преследует две цели – выявление значимых и мультиколлинеарных независимых переменных.

Первая строка матрицы содержит коэффициенты корреляции между зависимой (y) и независимыми переменными (х1, х2, …, xm). Коэффициенты этой строки анализируются с целью выявления значимых независимых переменных. Значимость независимой переменной здесь понимается с точки зрения влияния её на зависимую переменную. Если проверка гипотезы Н0: yxi = 0 покажет, что

эта гипотеза не отклоняется, то это означает, что соответствующая независимая переменная незначимо влияет на зависимую переменную, т. е. незначима, и в уравнение регрессии включать её не рекомендуется. Отметим, что подобные выводы предварительные и правомерны лишь на начальном этапе анализа информации, на самом деле взаимосвязи здесь более сложные, о чём речь ниже.

Второй этап анализа матрицы парных коэффициентов корреляции заключается в выявлении мультиколлинеарности среди независимых переменных. Идеальным условием реализации регрессионного анализа является независимость между собой независимых переменных. Но это практически никогда не выполняется, и уж совсем нежелательно, чтобы между независимыми переменными наблюдалась тесная корреляционная взаимосвязь. В этом случае говорят о коллинеарности переменных. Считается, что две случайные переменные коллинеарные, если коэффициент корреляции между ними не менее 0,7. Если таких переменных несколько, то говорят о мультиколлинеарности.

24

Мультиколлинеарность для регрессионного анализа нежелательна, и, как было отмечено, её выявление является одной из задач анализа матрицы парных коэффициентов корреляции.

Для этого просматривается оставшаяся часть матрицы R (кроме первой строки) и выделяются коэффициенты, по величине 0,7. Они и укажут на коллинеарные переменные. Обычно в уравнении регрессии оставляют те из значимых коллинеарных переменных, которые слабее связаны с другими зависимыми переменными.

2.1.2. Частная и множественная корреляция

Частная и множественная корреляция обычно рассматриваются при изучении совокупности многомерных измерений. Рассмотрим её кратко на промере трёхмерного пространства.

Пусть имеем три переменные – x, y, z.

Частным коэффициентом корреляции между x и y при фиксированном значении z или, другими словами, при исключении влияния на них переменной z является величина, определяемая из выражения:

Остальные частные коэффициенты корреляции определяются путём замены в приведённой формуле соответствующих индексов.

Частные коэффициенты корреляции можно рассчитать, рассматривая корреляцию не непосредственно между переменными, а между отклонениями, в которых влияние других переменных исключено.

Для трёх переменных это выглядит следующим образом. Пусть х и у корреляционно зависят от z. Выразим эту зависимость в виде: = f1(z), = f2(z). Рассмотрим разности ех = (x-) и еу = (y- ). Ясно, что в них влияние переменной z исключено, поэтому коэффициент корреляции между остатками ех и еу будет отражать связь между исходными переменными х и у с исключением влияния переменной z. Таким образом reч e y = rxy / z .

Частные коэффициенты корреляции обладают всеми свойствами парных коэффициентов корреляции. Они служат показателями чистой линейной корреляционной связи между переменными с исключением влияния учтённых переменных.

Частная корреляция очищает взаимосвязи между переменными от опосредованных зависимостей и помогает обнаружить величины, которые усиливают или ослабляют связи между конкретными переменными.

25

В развитие дальнейшего рассмотрения корреляции распространим понятие корреляционной связи на более чем две переменные. Тесноту линейной корреляционной связи между одной переменной и несколькими другими измеряют с помощью коэффициента множественного корреляции. Множественный коэффициент корреляции, например, между величиной z и двумя величинами x и y определяется по формуле

Такой коэффициент заключён между нулём и единицей и равен единице, когда связь между величинами z и (x,y) является линейной функциональной, и равен нулю, если линейная связь между z и (x,y) отсутствует. Другие множественные коэффициенты корреляции определяются путём замены соответствующих индексов в приведённой формуле.

Коэффициент множественный корреляции можно определить, рассчитав коэффициент корреляции между z и , где = f(x,y) – модельные значения z, вычисленные по уравнению регрессии от х и у. Таким образом = .

Понятия частного и множественного коэффициентов корреляции можно распространить на случай более 3 переменных. Вычисляются они на основе матрицы парных коэффициентов корреляции.

Так, коэффициент частной корреляции между переменными xi и xj при фиксированных значениях всех остальных рассматриваемых переменных X(i,j)

рассчитывается из соотношения

ri,j.X(i,j) = –Ri,j / (RiiRjj)1/2,

а коэффициент множественной корреляции между переменной xi и всеми другими переменными X(i) , т. е. коэффициент Ri.X(i) рассчитывается из соотношения

Здесь Rkl – алгебраическое дополнение для элемента rkl в определителе корреляционной матрицы R анализируемых признаков, а det R – определитель этой матрицы.

При определении значимости частных коэффициентов корреляции пользуются теми же методами, что и для парных коэффициентов корреляции, уменьшая число степеней свободы на число исключаемых переменных, а для множественных коэффициентов корреляции используется F-статистика:

где m – число анализируемых переменных.

26

При верности гипотезы о равенстве нулю коэффициента множественной корреляции F-статистика следует распределению Фишера с числом степеней свободы числителя, равным m, и знаменателя, равным n – m – 1.

Квадрат коэффициента множественной корреляции называется коэффициентом множественной детерминации. Коэффициент множественной детерминации показывает долю вариации одной переменной, обусловленную изменением других, включенных в анализ, переменных.

2.2. Множественный регрессионный анализ

Если в регрессионном анализе рассматривается пара переменных (одна зависимая, одна независимая), то говорят о парной или простой регрессии. Если независимых переменных более одной, то говорят о множественной регрессии.

2.2.1. Метод наименьших квадратов и его предпосылки

Рассмотрим уравнение линейной множественной регрессии. Уравнение генеральной совокупности или модель регрессии запишем в виде

t – значения случайного члена уравнения регрессии.

Предполагается, что εt независимы и нормально распределены с нулевым математическим ожиданием и постоянной дисперсией 2 , т. е. t N(0, 2 ).

Термины «зависимая» и «независимые» для переменных не совсем удачны и означают лишь, что в этом случае значения зависимой переменной оцениваются на основе известных значений независимых переменных.

Приведём предпосылки спецификации классической регрессионной модели:

эндогенная, зависимая переменная объясняется m экзогенными, независимыми переменными;

в общем случае уравнение регрессии включает константу;

объём выборки n должен быть значительно больше числа объясняющих переменных m (считается, что каждый регрессор должен быть обеспечен не менее 6–7 наблюдениями);

разность n–m–1 называется числом степеней свободы модели; чем она больше, тем надёжнее результаты оценивания;

27

параметры уравнения регрессии k должны быть постоянными для всей выборки; это положение зачастую определяет выборку.

Кроме предпосылок спецификации модели необходимо выполнение ещё и предпосылок метода наименьших квадратов (МНК). Как известно, оценки параметров модели линейной регрессии обычно рассчитываются на основе МНК. Доказано, что эти оценки будут «хорошими», т.е. несмещёнными, эффективными и состоятельными, если будут выполняться следующие

в остатках наблюдается гомоскедастичность; в противном случае – гетероскедастичность;

случайные отклонения t и s независимы друг от друга для t s, в этом случае говорят, что в остатках отсутствует какая-либо автокорреляция;

Последняя предпосылка не влияет на качество оценок и необходима проверки статистических гипотез и построения интервальных оценок.

Одна из задач эконометрики – тестирование выполнимости предпосылок и

выборочная реализация случайного процесса t .

Представим уравнение генеральной совокупности и оценённое уравнение регрессии в матричной форме. Введём следующие обозначения:

Тогда уравнения регрессии (2.1) и (2.2) в матричной форме примут вид

Y = X + и Y = Xb + e. (2.3)

МНК-оценки параметров уравнения (2.1) рассчитываются из условия минимизации по b квадратичной формы:

Q(b) = e = (Y – Xb)T(Y – Xb) = YTY – 2YTXb – bTXTXb.

Продифференцируем Q(b) по b и приравняем результат к нулю:

28

Это и есть МНК-оценка параметров уравнения (2.1).

Кроме того, известно, что несмещённая оценка дисперсии случайного члена t равна

где yˆ – оценённые по уравнению (2.2) значения зависимой переменной.

2.2.2 Свойства МНК-оценок

Остановимся более подробно на свойствах полученных оценок. Относительно уравнения множественной регрессии можно высказать те же предположения 1 – 4, что и для простой регрессии (заменив независимую переменную векторов независимых переменных), в том числе и предположения, лежащие в основе теоремы Гаусса-Маркова.

Рассмотрим математическое ожидание полученных оценок.

Здесь предполагается, что матрица Х детерминирована, а М() = 0. Таким образом, если регрессоры и остатки некоррелированны и математическое ожидание остатков равно нулю, то МНК-оценки являются несмещёнными. При доказательстве этого положения не использовались предположения 3 и 4 пункта 1.1, откуда следует, что МНК-оценки являются несмещённой до тех пор, пока регрессионные остатки имеют нулевое среднее и независимы от всех объясняющих переменных, даже если в них наблюдается гетероскедастичность и автокорреляция.

Подсчитаем ковариационную матрицу полученных оценок. При этом будем

Итак, Cov(b) = (XTX)-1. На главной диагонали этой матрицы находятся дисперсии соответствующих оценок, т. е. D() = .

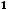29

2.2.3. Показатели точности уравнения регрессии и оценок его параметров

При анализе уравнения регрессии сначала проверяется значимость уравнения регрессии в целом. Для решения этой задачи используется процедура дисперсионного анализа, основанная на разложении общей суммы квадратов отклонений зависимой переменной (SST – Sum. Squared total) на две составляющие: одна из которых – за счёт регрессионной зависимости (SSM – Sum. Squared model), другая – за счёт остаточного члена (SSR – Sum. Squared residual):

SST = SSM + SSR

или

Следует иметь в виду, что это соотношение верно, если в уравнении регрессии присутствует константа. Разделив суммы квадратов отклонений на соответствующие числа степеней свободы, получим суммы квадратов на одну степень свободы или средние квадраты, которые являются оценками дисперсии 2 зависимой переменной y или остатков в условиях разных предпосылок. Одна из этих оценок (MSM = SSM/m) рассчитывается в предположении, что все коэффициенты в модели регрессии равны нулю (Ho: 1 = 2 =…= m =0), а другая (MSR = SSR/(n–m–1)) – в предположении, что не все коэффициенты регрессии равны нулю. Затем эти оценки сравниваются по F-статистике (F =

MSMMSR ), которая в случае выполнимости предпосылок МНК и верности нулевой

гипотезы имеет распределение Фишера с числом степеней свободы числителя, равным m и знаменателя – (n – m – 1). Расчётное значение F-статистики сравнивается с критическим и если F , то нулевая гипотеза отклоняется, и уравнение регрессии признаётся значимым.

Вернёмся ещё раз к MSR. Этот показатель является одной из характеристик точности уравнения регрессии. Его называют остаточной дисперсией и обозначают S ост2 . . Можно показать, что MSR является несмещённой оценкой

дисперсии 2 .

MSR также используется при вычислении других показателей точности уравнения регрессии. Например, корень квадратный из MSR называется стандартной ошибкой оценки по регрессии (Sy,x) и показывает, какую ошибку в среднем мы будем допускать, если значение зависимой переменной будем оценивать по найденному уравнению регрессии при известных значениях независимых переменных. Имеем

30