
5672
.pdf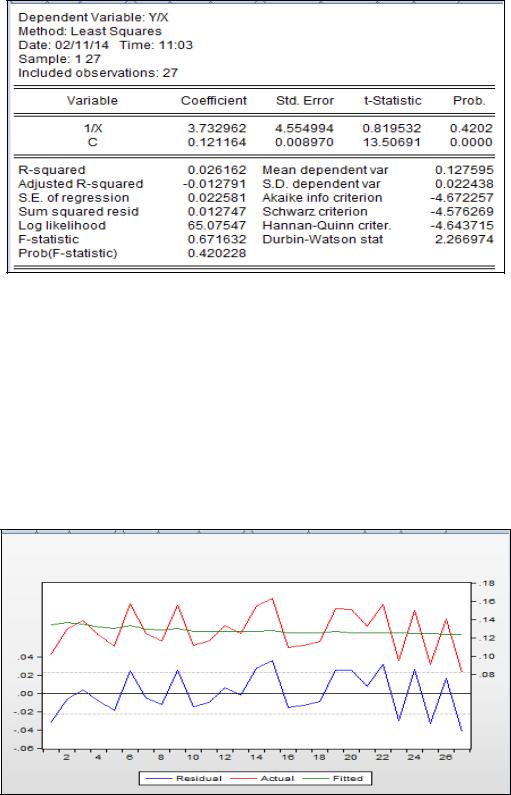
Рисунок 2.22 – Взвешенный МНК
Как отмечалось, коэффициенты этого уравнения нужно интерпретировать в рамках исходного уравнения регрессии, т. е. константа – это коэффициент при х в исходном уравнении. Он незначимо отличается от коэффициента в исходной модели. Аналогично можно сказать и об оценке его стандартной ошибки. Различие же в свободных членах здесь не существенно, т. к. эти оценки незначимо отличаются от нуля (и там и там расчётный уровень значимости больше 0,05).
Рисунок 2.23 – График остатков преобразованного уравнения регрессии
А вот от гетероскедастичности в остатках этим методом (взвешенным МНК) удалось избавиться, их разброс вокруг нуля стал равномерным (рисунок 2.23).
51

2.2.8. Стандартизованное уравнение множественной регрессии
Коэффициенты уравнения регрессии, как и всякие абсолютные показатели, не могут быть использованы в сравнительном анализе, если единицы измерения соответствующих переменных различны. Например, если y – расходы семьи на питание, х1 – размер семьи, а х2 – общий доход семьи, и мы определяем
зависимость типа |
ˆ = a + b |
x |
1 |
+ b x |
2 |
и b |
2 |
> b , то это не значит, что x |
2 |
|
|
y |
1 |
|
2 |
|
1 |
||||
сильнее влияет на y, |
чем х1, |
т. к. b2 – это изменение расходов семьи при |
||||||||
изменении доходов на 1 руб., а |
b1 – изменение расходов при изменении размера |
|||||||||
семьи на 1 человека. |
|
|
|
|
|
|
|
|
|
|
Сопоставимость коэффициентов уравнения регрессии достигается при рассмотрении стандартизованного уравнения регрессии:
|
|
|
|
|
|
|
|
y0 = 1x10 + 2x20 + … + |
mxm0 + е , |
|
|||||||||
где y0 |
и x0k – |
стандартизованные значения переменных y |
и xk: |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
0 |
|
y |
|
y |
, x |
0 |
x x k |
|
, |
|
||
|
|
|
|
|
|
|
|
|
Sy |
k |
Sx |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|||
Sy |
и S x |
k |
|
– стандартные отклонения переменных y и xk, |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
k |
(k=1, n ) |
– -коэффициенты уравнения |
регрессии |
(но не параметры |
|||||||||||||||
уравнения |
|
регрессии, |
в |
отличие |
от |
приведенных ранее |
обозначений). - |
||||||||||||
коэффициенты показывают, на какую часть своего стандартного отклонения (Sy)
изменится |
зависимая переменная y, если |
независимая |
переменная xk |
||
изменится |
на величину своего стандартного |
отклонения |
(S x |
k |
). Оценки |
|
|
|
|
|
|
параметров уравнения регрессии в абсолютных показателях (bk) и β- коэффициенты связаны соотношением:
βk |
bk |
Sx |
k |
. |
|
|
|||
|
|
Sy |
||
-коэффициенты уравнения регрессии в стандартизованном масштабе создают реальное представление о воздействии независимых переменных на моделируемый показатель. Если величина -коэффициента для какой-либо переменной превышает значение соответствующего -коэффициента для другой переменной, то влияние первой переменной на изменение результативного показателя следует признать более существенным. Следует иметь в виду, что стандартизированное уравнение регрессии в силу центрирования переменных не имеет свободного члена по построению.
Для простой регрессии -коэффициент совпадает с коэффициентом парной корреляции, что позволяет придать коэффициенту парной корреляции смысловое значение.
При анализе воздействия показателей, включённых в уравнение регрессии, на моделируемый признак, наравне с -коэффициентами используются также
52
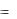
коэффициенты эластичности. Например, показатель средней эластичности рассчитывается по формуле
Эk |
bk |
|
xk |
|
||
|
|
|
|
|
||
|
y |
|
||||
|
|
|
|
|
||
и показывает, на сколько процентов в среднем изменится зависимая переменная, если среднее значение соответствующей независимой переменной изменится на один процент (при прочих равных условиях).
2.2.9. Дискретные переменные в регрессионном анализе
Как правило, переменные в регрессионных моделях имеют непрерывные области изменения. Однако теория не накладывает никаких ограничений на характер таких переменных. Довольно часто возникает необходимость учитывать в регрессионном анализе влияние качественных признаков и зависимость таковых от разных факторов. В этом случае появляется необходимость вводить в регрессионную модель дискретные переменные. Дискретные переменные могут быть как независимыми, так и зависимыми. Рассмотрим эти случаи по-отдельности. Сначала рассмотрим случай дискретных независимых переменных.
Фиктивные переменные в регрессионном анализе
Чтобы включить в регрессию в качестве независимых переменных качественные признаки, их надо оцифровать. Одним из методов их оцифровки является использование фиктивных переменных. Название не совсем удачное – никакие они не фиктивные, просто для этих целей более удобно использовать переменные, принимающие всего два значения – ноль или единица. Вот их и назвали фиктивными. Обычно качественная переменная может принимать несколько значений-уровней. Например, пол – мужской, женский; квалификация
– высокая, средняя, низкая; сезонность – I, II, III и IV кварталы и т. д. Существует правило, согласно которому для оцифровки таких переменных нужно вводить количество фиктивных переменных, числом меньше на единицу, чем число уровней моделируемого показателя. Это необходимо для того, чтобы такие переменные не оказались бы линейно зависимыми.
В наших примерах: пол – одна переменная, равная 1 для мужчин и 0 – для женщин. Квалификации имеет три уровня, значит, нужны две фиктивные переменные: например, z1 = 1 для высокого уровня, 0 – для других; z2 = 1 для среднего уровня, 0 – для других. Третью аналогичную переменную вводить нельзя, т. к. в этом случае они оказались бы линейно зависимыми (z1 + z2 + z3 = 1), определитель матрицы (XTX) обратился бы в нуль и найти обратную матрицу
53
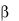
(XTX)-1 не удалось бы. Как известно, оценки параметров уравнения регрессии определяются из соотношения: 

 TX)-1XTY).
TX)-1XTY).
Коэффициенты при фиктивных переменных показывают, насколько значение зависимой переменной отличается при анализируемом уровне по сравнению с отсутствующим уровнем. Например, если бы моделировался уровень зарплаты в зависимости от нескольких признаков и уровня квалификации, то коэффициент при z1 показал бы, насколько зарплата у специалистов с высоким уровнем квалификации отличается от зарплаты у специалиста с низким уровнем квалификации при прочих равных условиях, а коэффициент при z2 – аналогичный смысл для специалистов со средним уровнем квалификации. В случае с сезонностью пришлось бы вводить три фиктивных переменных (если рассматриваются квартальные данные) и коэффициенты при них показали бы, насколько величина зависимой переменной отличается для соответствующего квартала от уровня зависимой переменной для квартала, который не был введён при их оцифровке.
Фиктивные переменные кроме того вводятся для моделирования структурных изменений в динамике изучаемых показателей при анализе временных рядов.
Пример 4. Стандартизированное уравнение регрессии и фиктивные переменные
Рассмотрим пример использования стандартизированных коэффициентов и фиктивных переменных на примере анализа рынка двухкомнатных квартир на основе уравнения множественной регрессии при следующем наборе переменных:
PRICE – цена;
TOTSP – общая площадь;
LIVSP – жилая площадь;
KITSP – площадь кухни;
DIST – расстояние до центра города;
WALK – равна 1, если до станции метро можно дойти пешком и равна 0, если надо воспользоваться общественным транспортом;
BRICK – равна 1, если дом кирпичный и равна 0, если панельный;
FLOOR – равна 1, если квартира не на первом и не на последнем этаже и равна 0 в противном случае;
TEL – равна 1, если в квартире есть телефон и равна 1, если нет; BAL – равна 1, если есть балкон и равна 0, если балкона нет.
Расчёты проведены с помощью ППП STATISTICA (рисунок 2.23). Наличие -коэффициентов позволяет упорядочить переменные по степени их влияния на
зависимую переменную. Проведем краткий анализ результатов расчётов.
54
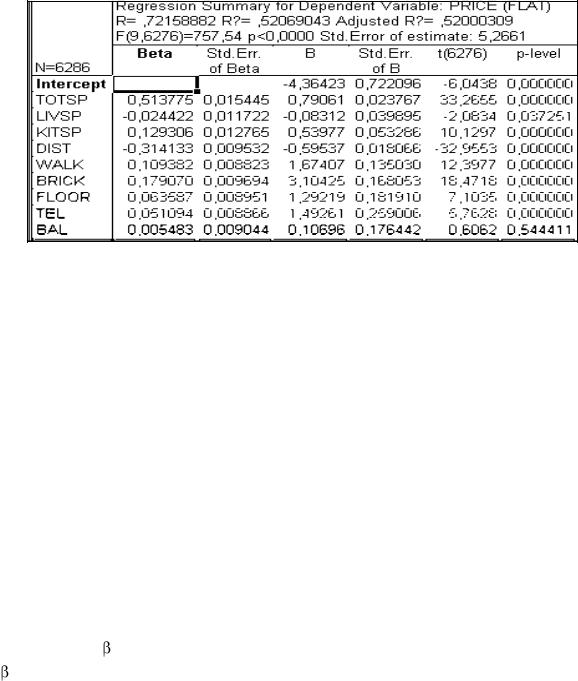
На основе статистики Фишера делаем вывод о значимости уравнения регрессии (р-level < 0,05). Обработана информация о 6 286 квартирах (n–m–1 = 6 276, а m = 9). Все коэффициенты уравнения регрессии (кроме при переменной BAL) значимы (р-величины для них < 0,05), а наличие или отсутствие балкона в этом случае существенно не сказывается на цене квартиры.
Рисунок 2.24 – Отчёт о рынке квартир на основе ППП STATISTICA
Коэффициент множественной детерминации равен 52%, следовательно, включённые в регрессию переменные обусловливают изменение цены на 52 %, а остальные 48 % изменения цены квартиры зависят от неучтённых факторов. В том числе и от случайных колебаний цены.
Каждый из коэффициентов при переменной показывает, насколько изменится цена квартиры (при прочих равных условиях), если данная переменная изменится на единицу. Так, например, при изменении общей площади на 1 кв. м цена квартиры в среднем изменится на 0,791 у.е., а при удалении квартиры от центра города на 1 км цена квартиры в среднем уменьшится на 0,596 у.е. и т. д. Фиктивные переменные (последние 5) показывают, на сколько в среднем изменится цена квартиры, если перейти с одного уровня этой переменной на другой. Так, например, если дом кирпичный, то квартира в нем в среднем на 3,104 у. е. дороже, чем такая же в панельном доме, а наличие телефона в квартире поднимает ее цену в среднем на 1,493 у. е. и т. п.
На основе -коэффициентов можно сделать следующие выводы. Наибольшим -коэффициентом, равным 0,514 является коэффициент при переменной «общая площадь», следовательно в первую очередь цена квартиры формируется под влиянием её общей площади. Следующий фактор по степени влияния на изменение цены квартиры является расстояние до центра города, затем
материал, из которого построен дом, затем площадь кухни и т. д.
55
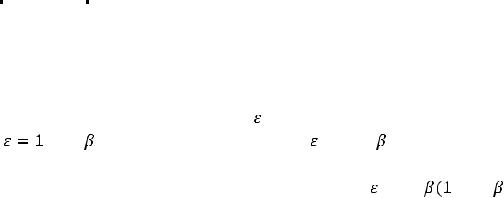
2.2.10. Дискретные (качественные) зависимые переменные
Рассмотрим наиболее простой вариант, когда в качестве зависимой дискретной переменной выступает бинарная переменная, принимающая только два значения, обычно нуль или единица. В этом случае уравнение регрессии называется моделью бинарного выбора в отличие от модели множественного выбора.
Выдвигая различные предположения о характере зависимости бинарной зависимой переменной от значений независимых переменных, можно получить разные модели. В дальнейшем рассмотрим три модели – линейную модель вероятности, probit- и logit-модели.
Линейная модель вероятности
Воспользуемся обычной линейной моделью регрессии: У = ХT +
+ 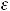 . Т. к. У может принимать только два значения 0 или 1 и М(
. Т. к. У может принимать только два значения 0 или 1 и М(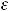 ) = 0 (М – знак математического ожидания), то
) = 0 (М – знак математического ожидания), то
М(У) = 1 Р(У = 1)+0 Р(У = 0) = Р(У = 1) = ХT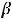 .
.
Таким образом, исходная модель может быть записана в виде
Р(У = 1) = ХT ,
,
поэтому её называют линейной моделью вероятностей.
В отличие от обычной линейной регрессионной модели эта модель обладает
рядом |
особенностей. |
Во-первых, ошибка |
может |
принимать |
только два |
||||||||
значения – |
|
ХT |
с вероятностью Р(У=1) и |
= |
|
ХT с вероятностью |
|||||||
|
|
||||||||||||
1 |
|
|
Р(У=1). Это не позволяет считать, что ошибка распределена по |
||||||||||
|
|
||||||||||||
нормальному закону. К тому же дисперсия ошибки равна D( ) = ХT |
|
|
ХT ), |
||||||||||
|
|
||||||||||||
т. е. зависит от регрессоров, а значит, имеем модель с гетероскедастичными остатками. Кроме того, прогнозные значения зависимой переменной могут не лежать внутри отрезка [0,1], что значительно снижает ценность такой модели для практических расчётов. Обычно такую модель используют для первичной обработки данных для сравнения с результатами более сложных моделей.
Probit- и Logit-модели
В линейной модели вероятностей вероятность события является линейной функцией независимых переменных, что является её основным недостатком. Этот недостаток можно преодолеть, записав вероятность как функцию, область значений которой лежит в интервале [0,1]. Известно, что таким свойством
56

обладают функции стандартного нормального и логистического распределений:
F(u) = Ф(u) = 




 и F(u) =
и F(u) = 
 =
= 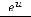 , где u = ХT
, где u = ХT .
.
Соответственно такие модели называются probit- и logit-моделями.
Вопрос о том, какую модель предпочесть, решается исследователем, тем более что для достаточно близких по модулю к нулю значений u обе функции дают примерно одинаковые результаты. Логистическая функция более проста в вычислительном аспекте, поэтому используется чаще.
Рассмотрим более подробно эту модель. Пусть р = Р(А) – вероятность некоторого события. Отношение  называют шансами этого события.
называют шансами этого события.
Например, если р = 1/3, то р/(1 |
|
р) = ½, и шансы |
на |
то, что событие А |
|||||||||
|
|||||||||||||
произойдёт, равны ½ (или в два раза ниже). Логарифм отношения р/(1 |
|
р) |
|||||||||||
|
|||||||||||||
называют логитом, logit(p) = ln(p/1 |
|
p). Если р , то больше щансов, |
что |
||||||||||
|
|||||||||||||
событие А произойдёт. Пусть теперь р = Р(у=1). В логит |
|
модели р = |
|
Т |
) = |
||||||||
|
|
|
|||||||||||
exp(( Т )/(1+ Т )), 1 |
|
р = 1/(1+ Т ), так что logit(p) = |
Т |
, т. е. логит |
|
модель |
|||||||
|
|
|
|
||||||||||
линейна в отношении логита. Отсюда и большая простота этой модели в вычислительном аспекте.
Поскольку эти модели не линейны по параметрам, то для оценивания их параметров используется метод максимального правдоподобия, который здесь не обсуждается. Вычисления по этому методу следует предоставить вашему компьютерному пакету.
Оценка качества подгонки данных моделью в этом случае отличается от аналогичной в линейном МНК. Вместо коэффициента множественной
детерминации вычисляется псевдо R2 = 1 
 , где
, где 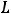 и
и  – соответственно
– соответственно
значения функции правдоподобия, когда не все коэффициенты регрессии равны нулю и когда все коэффициенты регрессии равны нулю. В EViews эта статистика называется McFadden R-squared.
Известно, что значения этого показателя находится в интервале [0,1] и чем ближе его значение к единице, тем точнее уравнение. Здесь речь идёт о качестве подгонки наблюдаемых частот зависимой переменной расчётными вероятностями или насколько точно модель предсказывает наблюдаемые частоты.
Ещё один тест на точность модели, выдаваемый пакетом EViews, называется LR-тестом и рассчитывается из соотношения LR = 2(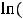
 ) ln(
) ln( )). Здесь тестируется гипотеза о том, что все коэффициенты модели равны нулю. Если эта гипотеза верна, то LR-статистика следует хи-
)). Здесь тестируется гипотеза о том, что все коэффициенты модели равны нулю. Если эта гипотеза верна, то LR-статистика следует хи- распределению с m степенями свободы.
распределению с m степенями свободы.
57
Пример 5. Модель бинарного выбора Рассмотрим пример моделирования наличия компьютера у индивидуума в
зависимости от его социального статуса (Ben Vogelvang, 2005).
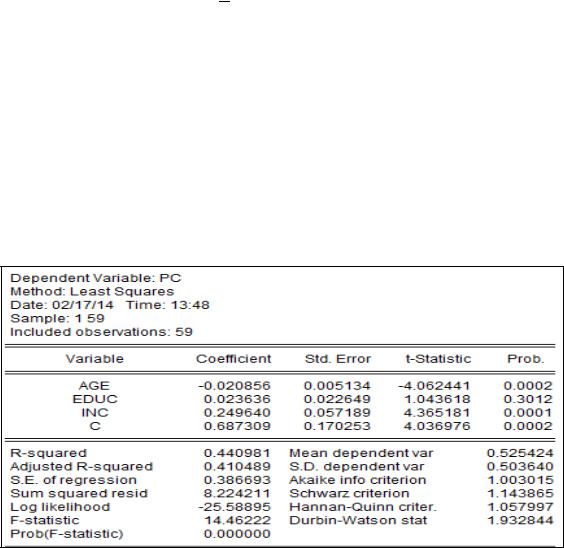
Переменная отклика (зависимая переменная) PC равна нулю, если индивид не имеет компьютера, и равна единице, если компьютер есть. Зависимые переменные: EDUC – образование (сколько лет учился), INC – доход (от менее 10 000 до более 50 000 с интервалом в 10 000, т. е. принимает значения, равные 0,1,2,3,4,5) и AGE – возраст (18 81 год). Было опрошено 59 человек.
Линейная модель вероятностей показана на рисунке 2.25. Поскольку образование имеет малое влияние на факт наличия компьютера, попробуем скорректировать оценки ошибок по форме Уайта (рисунок 2.26). Как видим, незначимость образования осталась, хотя расчётный уровень значимости уменьшился. Получили, что изменение показателя наличия компьютера описывается изменением этих трёх признаков на 44%.
Из графика (рисунок 2.27) видно, что некоторые расчётные значения переменной отклика линейной модели вероятностей вышли из интервала [0,1] (есть и больше единицы и отрицательные значения), что «говорит» о недостатках этой модели.
Рисунок 2.25 – Исходная линейная модель вероятностей
58
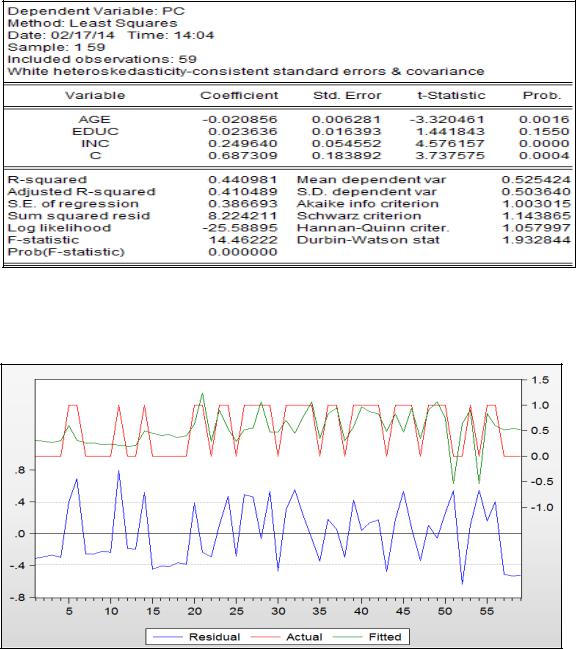
Рисунок 2.26 – Линейная модель вероятностей со стандартными ошибками в форме Уайта
Рисунок 2.27 – График фактических, расчётных значений и остатков линейной модели вероятностей
Рассмотрим этот же пример для logit-модели. Для этого в окне спецификации модели (заставка «Specificftion») в позиции «Method» выбираем «BINARY» – модели бинарного выбора и в позиции «Binary estimation method» ставим точку «Logit» (рисунок 2.28). Тем самым заказали оценку параметров logit-модели.
59
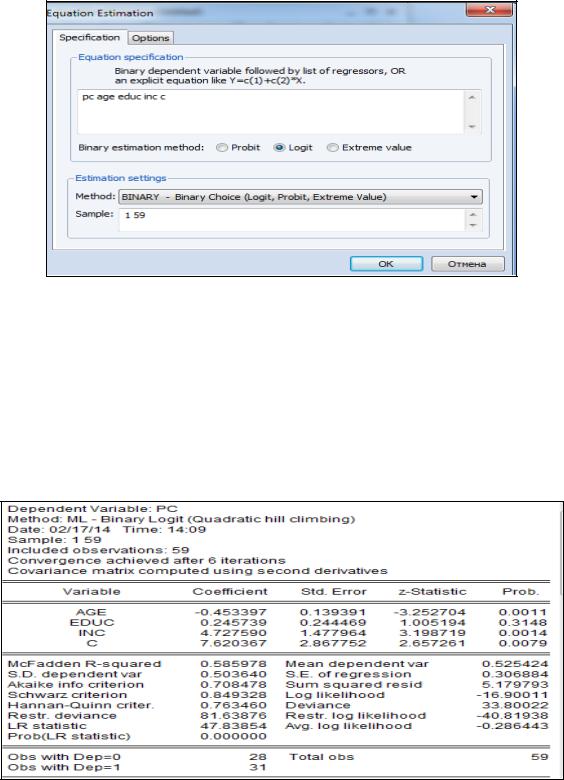
Рисунок 2.28 – Выбор метода оценивания модели бинарного выбора
После оценки получили рисунок 2.29. Псевдо R-квадрат модели равен 0,58, что «говорит», что точность предсказания удовлетворительная, а LRстатистика имеет расчётный уровень значимости меньше 0,05, что говорит о том, что уравнение регрессии значимо. Кроме того, в отчёте указано, что в выборке представлены 28 человек, не имеющих компьютера и 31 – имеющий компьютер, общее число наблюдений – 59 (см. нижнюю часть рисунка 2.29).
Рисунок 2.29 – Отчёт об оценке модели бинарного выбора
По графику фактических, расчётных значений и остатков logit-модели (рисунок 2.30) видно, что эта модель более точно описывает переменную
60
