5672

отклика и все её значения попали в интервал [0,1]. Так что данную модель можно признать адекватной исходным данным.

Чтобы сравнить коэффициенты при переменных в линейной модели вероятностей и в logit-модели, воспользуемся правилом Амемийя, в соответствии с которым коэффициенты logit-модели надо уменьшить в 4 раза и к константе добавить 0,5. Получим

-----------------------------------------------------------------------------------------------------

Как видим, все оценки logit-модели больше оценок линейной модели вероятностей.

Рисунок 2.30 – График фактических, расчётных значений и остатков logit- модели

EViews представляет возможность спрогнозировать по оценённой модели вероятность наступления события при фиксированных значениях независимых переменных. Допустим, надо рассчитать вероятность того, что индивид в возрасте 40 лет, проучившийся 5 лет и имеющий доход на уровне 2 (от 20 000 до 30 000) имеет компьютер. Для этого в окне команд надо набрать уравнение оценённой модели и подставить в неё значения независимых переменных Нажав «Enter», получим 0,542. Это и есть оценённая вероятность (рисунок 2.31).

61

Рисунок 2.31 – Прогноз переменной отклика

По линейной модели вероятностей получим р = 0,687 0,021 40 + 0,024 5 + 0,250 2 = 0,467. Здесь различие небольшое. Но если взять более молодого (35 лет) и менее грамотного (образование 1 год) индивида с более высоким доходом (свыше 50 000), то получим, что вероятность иметь компьютер по logit-модели практически равна 1 (рисунок 2.32), а по линейной модели вероятностей равна р = 0,687 0,021 35 + 0,024 1 + 0,250 5 = 1,23, что лишено смысла.

Рисунок 2.32 – Прогноз переменной отклика для других значений независимых переменных

62

Отметим, что здесь был рассмотрен наиболее простой вариант logit-модели

– модель бинарного выбора. В эконометрической литературе можно найти более сложные модели, которые здесь не рассматриваются.

2.2.11. Пошаговый регрессионный анализ

Отбор переменных в уравнение множественной регрессии может осуществляться в несколько этапов. На первом этапе подобный отбор осуществляется исходя из качественного анализа изучаемого социальноэкономического явления, без каких бы то ни было ограничений на переменные. На втором этапе на основе, например, анализа матрицы парных коэффициентов корреляции можно отсеять незначимые факторные переменные, если это не входит в противоречие с логикой изучаемого явления. И только на третьем этапе провести строгий отбор с использованием метода пошагового выбора переменных.

При использовании этого метода отбор переменных происходит исходя только из формальных статистических критериев. Это основной недостаток метода. Подобные процедуры включены во многие статистические пакеты прикладных программ и предусматривают три варианта их реализации.

Процедура “вперёд” (Forward) начинает «работать» с пустой моделью и последовательно включает в модель только значимые переменные. При этом на каждом шаге значимость каждой переменной определяется заново. Осуществляется это в разных программах по-разному, например, в Statgraphics на основе коэффициентов частной корреляции и рассчитанных для них статистик Фишера, а в EViews – либо на основе t-статистик, либо на основе p- value. Процедура включения переменных в модель заканчивается, если на очередном шаге наибольшее значение критерия Фишера или t-статистики (p- value) будет меньше граничного. Граничное значение либо устанавливается исследователем, либо определяется по умолчанию. Если в результате реализации этого метода переменная на каком-либо шаге была включена в уравнение, то она там остаётся до конечного шага алгоритма, даже если она потом окажется незначимой, поэтому в этом варианте процедуры пошаговой регрессии есть риск включить в регрессию незначимую переменную.

Процедура ”назад” (Backward) начинает «работать» с полной моделью и последовательно исключает из неё незначимые переменные. Значимость оставшихся переменных здесь пересчитывается также на каждом шаге. В этом случае на каждом шаге из уравнения регрессии будут исключаться только незначимые независимые переменные. Если в этой процедуре переменная на каком-либо шаге была исключена из уравнения, но потом на каком-то шаге она стала значимой, то она не будет включена в уравнения до конца работы

63

алгоритма, поскольку в дальнейшем анализе она не участвует, поэтому здесь есть риск исключить из регрессии значимую переменную.

Пошаговая процедура (Stepwise) включения-исключения переменных состоит в сочетании двух уже рассмотренных методов. Здесь после очередного включения-исключения переменной происходит перерасчёт значимости и включённых и исключённых переменных и, если какая-либо ранее включённая (исключённая) переменная оказывается незначимой (значимой), то она исключается из уравнения или включается в него.

В большинстве случаев эти три метода дают одинаковый конечный результат. Применение метода пошагового выбора переменных позволяет упростить уравнение регрессии без значимого ухудшения его точности. К тому же подобные процедуры исключают возможность включения в регрессию коллинеарных факторных переменных.

Пример 6. Пошаговый регрессионный анализ Рассмотрим пример анализа объёма реализации продукции фирмой (у) в

зависимости от расходов на рекламу (х1), цены продукции (х2) в фирме и у конкурента (х3), а также от индекса потребительских расходов (х4) за 4 года поквартально. Расчёты будем вести в EViews,

Оценённое уравнение регрессии с использованием обычного МНК представлено на рисунке 2.31.

Рисунок 2.33 – Отчёт об использовании обычного МНК

Как видим из отчёта (рисунок 2.31), две переменные в уравнении регрессии незначимы, т. е. объём реализации значимо не зависит от цены продукции на фирме и у конкурента. Проведём пошаговый регрессионный анализ, используя

64

процедуру «назад», которая последовательно будет исключать из регрессии незначимые переменные.

С этой целью в окне спецификации уравнения в позиции «Method» выберем процедуру «STEPLS – Stepwise Least Squares» (пошаговый МНК) (рисунок 2.34).

В первом окне устанавливаем имя зависимой переменной и константу, а во втором – список независимых переменных. После этого в заставке «Options» (рисунок 2.35) выбираем метод реализации пошагового МНК «Backwards назад» и критерий остановки работы метода по p-value = 0.05. Другие установки этого диалогового окна здесь не обсуждаются.

Рисунок 2.34 – Выбор процедуры пошагового МНК

Рисунок 2.35 – Выбор метода пошагового МНК и критерия остановки

65

Реализация выбранного метода показана на рисунке 2.36. Как видим, в уравнении регрессии осталось две переменные (х4 и х1) и обе они значимые. И хотя R-squared несколько уменьшился, по информационным критериям полученное уравнение предпочтительнее исходного (значения этих критериев уменьшилось).

В нижней части отчёта указана последовательность исключения переменных из уравнения, а в примечании указано, что расчётный уровень значимости (p- value) и последующий тесты для выводимых переменных не отражены в процедуре пошагового выбора.

Рисунок 2.36 – Отчёт о пошаговом МНК

Глава 3. Стохастические объясняющие переменные в регрессионном анализе

3.1. Инструментальные переменные

Одной из предпосылок МНК (в случае стохастических регрессоров) является требование, чтобы регрессоры и остатки были независимыми. Как было показано выше, если при этом математическое ожидание остатков равно нулю, МНК-оценки параметров уравнения регрессии будут несмещёнными. Одним из путей преодоления этой трудности (смещённость оценок вектора параметров) является использование других независимых переменных, которые носят название инструментальные переменные. Для получения состоятельных оценок

66

в этом случае надо, чтобы инструментальные переменные обладали двумя свойствами:

•новые независимые переменные должны быть тесно связаны с исходными независимыми переменными;

•новые переменные не должны быть связаны с остатками модели. Рассмотрим эти вопросы подробнее. Пусть исходная модель, как и раньше,

описывается равенством Y = X + . При этом установлено, что хотя бы один из регрессоров коррелирован с остатками модели. Предположим, что задана матрица Z размера – матрица инструментальных переменных, причём k x k матрица ZTX обратима (здесь n – число наблюдений, k – число регрессоров, включая константу). Тогда по определению оценкой параметров с помощью инструментальных переменных называется вектор 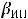= (ZTX)-1ZTY.

Можно показать, что эта оценка является состоятельной, хотя в общем случае может быть смещённой и не эффективной, поскольку зависит от Z.

Типичными ситуациями, когда требуется использование инструментальных переменных, является наличие ошибок в измерениях независимых переменных или наличие лаговых переменных в качестве независимых переменных, если остатки модели автокоррелированы. Кроме того, метод инструментальных переменных используется при анализе системы одновременных эконометрических уравнений, когда одни и те же переменные одновременно являются зависимыми в одних уравнениях и независимыми в других. Можно показать, что применение стандартного МНК в этих случаях будет приводить к смещённым и несостоятельным оценкам.

Рассмотрим один из таких случаев, когда предпосылка о независимости регрессоров и остатков нарушается. Пусть рассматривается уравнение регрессии, в котором в качестве регрессора выступает лагированная зависимая переменной и остатки при этом автокоррелированы. Тогда анализируемая модель имеет вид

yt = + xt + yt-1 + ,

где xt – единственная объясняющая переменная. Известно, что если регрессоры

автокорелированности связано с , следовательно, регрессор yt-1 и остаток также зависимы. Таким образом, если 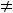0, то МНК больше не приводит к несмещённым и состоятельным оценкам для параметров исходной модели.

67

Метод оценивания с помощью инструментальных переменных является обобщением обычного МНК. Выбор самих инструментальных переменных – не совсем простая задача. Её решение зависит от конкретной ситуации. Может оказаться, что вообще не удаётся найти инструментальных переменных, а может существовать и несколько таких инструментов.

Идея метода инструментальных переменных заключается в следующем. Сначала осуществляем регрессию каждого xj на Z и находим расчётные значения , j = 1,…,k. Будем считать их новыми независимыми переменными, и оценка по методу инструментальных переменных вектора параметров строится с помощью обычной регрессии y на , j = 1,…,k. Таким образом, МНК применяется здесь дважды – сначала для построения регрессоров , j = 1,…,k, а затем для нахождения оценки . Эта процедура носит название двухшагового МНК.

Следует иметь в виду, что не для каждой независимой переменной необходимо строить инструмент. Если какая-либо независимая переменная не коррелирует с остатками, то она сама для себя может служить инструментом.

Тест Хаусмана служит для проверки того, надо ли применять инструментальные переменные или достаточно обойтись обычным МНК. В этом тесте нулевой гипотезой является предпосылка, что регрессоры и остатки независимы. Альтернативная гипотеза – зависимые.

Рассчитываются два вида оценок вектора параметров модели – обычным МНК () и с помощью инструментальных переменных (). При нулевой гипотезе обе эти оценки несмещённые и состоятельны, а при альтернативной – несмещённой оценкой является только оценка, рассчитанная с помощью инструментальных переменных. Так что при нулевой гипотезе разность этих оценок ( – 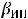) стремится к нулю и при соответствующей нормировке распределение этой разности асимптотически будет совпадать к каким-нибудь известным распределением.

Хаусман доказал, что при верности нулевой гипотезы асимптотически верно равенство Var( – ) = Var () – Var (), так что статистика

H = ( – )T(Var() – Var())-1( – ) при нулевой гипотезе асимптотически имеет хи-квадрат распределение с k степенями свободы.

Рассмотрим более общий случай, когда анализируются несколько эндогенных, т.е. определяемых внутри модели регрессоров. Пусть оценивается модель вида

Y = X1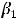 + X2 + ,

где X1 – матрица значений экзогенных объясняющих переменных, некоррелированных с остатками,

68

X2 – матрица значений эндогенных объясняющих переменных, коррелированных с остатками.

Чтобы оценить это уравнение, необходима инструментальная переменная для каждого элемента в векторе объясняющих переменных X2. Это означает, что если имеются, например, три эндогенных регрессора, то необходимо иметь, по крайней мере, три различных инструментальных переменных. Обозначая совокупность инструментальных переменных вектором Z2, оценку методом инструментальных переменных можно записать как = (ZTX)-1ZTY, где теперь X = (X1,X2), a Z =(X1,Z2).

Иногда всю матрицу Z рассматривают как матрицу инструментальных переменных. В этом случае, если переменная в матрице объясняющих переменных является экзогенной, то для неё не надо искать инструментальную переменную. Эта переменная используется в качестве своей собственной инструментальной переменной. Поэтому число инструментальных переменных должно быть не менее, чем число оцениваемых параметров. Если все переменные экзогенные, то при применении метода инструментальной переменной реализуется обычная МНК-оценка, где каждая переменная инструментирована сама собой.

3.2. Системы одновременных уравнений

Многие экономические взаимосвязи допускают моделирование одним уравнением. В этом случае предполагается, что между независимыми переменными хi и зависимой переменной у существует только прямая связь: хi у. Отсюда и терминология – зависимая и независимые переменные: у зависит от значений хi, а хi не зависят от значений у.

Применение отдельных уравнений регрессии в большинстве случаев предполагает, что независимые переменные можно изменять независимо друг от друга. Однако на практике изменение одной переменной не может происходить при неизменности других. Поэтому отдельно взятое уравнение не может характеризовать истинные влияния отдельных признаков на вариацию результирующей переменной.

Поэтому при исследовании социально-экономических явлений важное место занимает проблема описания связей между переменными не одним, а несколькими уравнениями. Отсюда возникла необходимость в использовании систем эконометрических уравнений.

Рассмотрим кратко проблемы, возникающие при анализе систем эконометрических уравнений на примере кейнсианской модели формирования доходов. Данная модель строится в предположении, что рассматривается закрытая экономика без государственных расходов:

69

– реальные инвестиции на душу населения.

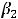
Коэффициент интерпретируется как предельная склонность к потреблению (0 и показывает, насколько больше люди будут потреблять, если их доход увеличится на единицу.

Особенность этой системы уравнений заключается в том, что в первом уравнении совокупный доход не является независимой переменной, а определяется вторым уравнением, которое является в этой модели определяющим уравнением для закрытой экономики и указывает, что совокупное потребление и совокупные инвестиции в сумме должны равняться совокупному доходу.

В дальнейшем переменные, определяемые вне модели, будем называть экзогенными, а те из них, которые определяются на основе модели, – эндогенными. Таким образом, 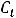и эндогенные переменные (определяются в модели совместно), а инвестиции экзогенны и определяются независимо от остатка, т. е. вне модели. Модель, состоящая из этих двух совместных уравнений, называется структурной формой модели.

Будем предполагать, что остатки являются независимыми и одинаково распределёнными по времени с нулевым средним и дисперсией , а и независимы (этим и определяется экзогенность инвестиций).

Тот факт, что является эндогенной, имеет свои последствия для оценивания функции потребления. Поскольку переменная влияет на в соответствии со вторым уравнением системы, то нельзя утверждать, что и 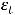являются некоррелированными. Следовательно, МНК оценка параметров этого уравнения будет смещённой и несостоятельной.

3.2.1. Оценивание параметров системы одновременных уравнений

Кратко рассмотрим проблему оценивания параметров системы одновременных уравнений, учитывая их специфику. В системах одновременных эконометрических уравнений одни и те же переменные одновременно выступают в одних уравнениях как экзогенные, а в других – как эндогенные. Поэтому оценивать их обычным МНК не представляется возможным в связи с тем, что в них не выполняется предпосылка независимости регрессоров и остатков.

Один из методов преодоления этой проблемы заключается в том, что структурную форму модели записывают в виде приведённой формы, выражая

70