5672

форму автокорреляции между ними, т. е. подразумевает нулевую корреляцию между различными регрессионными остатками. Вместе взятые эти предположения означают, что регрессионные остатки являются некоррелированными извлечениями из генеральной совокупности с распределением, имеющем нулевое математическое ожидание и постоянную дисперсию .

Предположение 2 утверждает независимость векторов значений независимой переменной и регрессионных остатков.

Известно, что если выполняются эти четыре предположения, то верна теорема Гаусса – Маркова, утверждающая, что в этом случае МНК-оценка b является наилучшей линейной несмещённой оценкой параметра β. Наилучшей в смысле эффективности.

Кроме сформулированных предположений вводится ещё одно, которое позволило бы сформулировать показатели точности уравнения регрессии и его оценок. Эта предпосылка утверждает, что остатки должны следовать нормальному закону распределения с нулевым математическим ожиданием и постоянной дисперсией .

В дальнейшем уравнение = a + bx будем называть выборочным уравнением y

регрессии или просто уравнением регрессии, а его коэффициенты, соответственно, свободным членом (а) и коэффициентом уравнения регрессии

(b).

Свободный член уравнения регрессии обычно не интерпретируется. Коэффициент регрессии показывает, насколько в среднем изменится зависимая переменная (в своих единицах измерения) при изменении независимой переменной на единицу своего измерения.

При этом, необходимо иметь в виду, что рассматриваемые коэффициенты

являются оценками параметров уравнения регрессии ~ = α + βx со всеми y

вытекающими отсюда последствиями, в том числе и необходимостью получения оценок точности уравнения регрессии и его параметров.

Рассмотрим некоторые из них.

1.2.2. Оценки точности уравнения регрессии и его параметров

Стандартная ошибка оценки по регрессии. Как было отмечено,

несмещённая оценка дисперсии остатков уравнения регрессии называется остаточной дисперсией

11

Корень квадратный из остаточной дисперсии называется стандартной ошибкой оценки по регрессии. Обозначается она обычно Sy,x и вычисляется по формуле

Стандартная ошибка оценки по регрессии показывает, насколько в среднем мы ошибаемся, оценивая значение зависимой переменной по найденному уравнению регрессии при фиксированном значении независимой переменной.

Оценка значимости уравнения регрессии (дисперсионный анализ регрессии). Для оценки значимости уравнения регрессии устанавливают, соответствует ли выбранная модель анализируемым данным. Для этого используется дисперсионный анализ регрессии. Основная его посылка – это

если в уравнении регрессии присутствует свободный член. В противном случае в

Второе слагаемое в правой части этого разложения уже встречалось и обсуждалось – это часть общей суммы квадратов отклонений, объясняемая действием случайных и неучтенных факторов. Первое слагаемое этого разложения – это часть общей суммы квадратов отклонений, объясняемая регрессионной зависимостью. Следовательно, если регрессионная зависимость между у и х отсутствует, то общая сумма квадратов отклонений объясняется

случае функциональной зависимости между у и х действие случайных факторов

Будучи отнесёнными к соответствующему числу степеней свободы эти

предположении отсутствия регрессионной зависимости, а другая – без такого предположения. Следовательно, если регрессионная зависимость отсутствует, то эти оценки должны быть близкими. Сравниваются они на основе F-отношения:

F = MSR/ MSE. Таким образом, F-статистика проверяет гипотезу о незначимости уравнения регрессии (H0: = 0), т. е. о том, что зависимости между анализируемыми переменными нет. Если верна нулевая гипотеза, то F- статистика следует распределению Фишера и, зная уровень значимости и число

12

степеней свободы числителя и знаменателя, можно определить критические значения этого распределения.

Расчётное значение F-статистики сравнивается с критическим значением (в нашем случае число степеней свободы числителя равно 1 (число регрессоров), а число степеней свободы знаменателя равно (n – 2)) с уровнем значимости . Если F < F, то гипотеза о незначимости уравнения регрессии не отклоняется, т.

е. не отклоняется гипотеза о том, что = 0, и уравнение регрессии признаётся незначимым. В этом случае надо либо изменить вид зависимости, либо пересмотреть набор исходных данных.

При компьютерных расчётах в некоторых статистических пакетах программ оценка значимости уравнения регрессии осуществляется на основе дисперсионного анализа в таблицах вида:

Таблица 1.1 – Дисперсионный анализ регрессии

расчётный уровень значимости. Если эта вероятность мала (меньше ), то нулевая гипотеза отклоняется.

В некоторых статистических пакетах программ значение F-статистики и вероятность для неё приводятся без показа процедуры их вычисления.

Если в уравнении регрессии нет константы, то в некоторых статистических пакетах F-статистика просто не вычисляется.

Интервальные оценки параметров уравнения регрессии. При использовании параметров уравнения регрессии в анализе и прогнозировании для них необходимо уметь строить интервальные оценки.

Доверительный интервал для коэффициента регрессии определяется из соотношения (b t / 2 Sb), где Sb – стандартная ошибка оценки коэффициента регрессии. Известно, что

Доверительный интервал для свободного члена уравнения регрессии определяется из соотношения (а t / 2 Sа), где Sа – стандартная ошибка оценки свободного члена уравнения регрессии. Известно, что

13

Интервальная оценка прогнозных значений определяется из подобного же соотношения, только в стандартную ошибку добавляется ещё стандартное отклонение , характеризующее рассеяние прогнозных значений зависимой переменной вокруг линии регрессии.

Проверка значимости параметров уравнения регрессии. Кроме проверки значимости уравнения регрессии в целом необходимо уметь проверять значимость каждого параметра уравнения регрессии в отдельности. Осуществляется это на основе t-статистик. Значения этих статистик рассчитываются из соотношений: ta = a/Sa, tb = b/Sb. Для этих статистик определяются критические значения или расчётные уровни значимости, на основе которых и принимаются решения о значимости или незначимости соответствующих параметров.

В случае парной линейной регрессии проверка значимости уравнения регрессии в целом и проверка значимости коэффициента уравнения регрессии по сути дела одно и то же, т. к. в том и другом случае проверяется одна и та же гипотеза о том, что коэффициент уравнения регрессии равен нулю. Кроме того, можно показать, что для парной линейной регрессии F =

Уравнение простой регрессии в компьютерных расчётах обычно выдаётся в виде следующей таблицы.

Таблица 1.2 – Уравнение простой регрессии

Пересечение и наклон – это другое название свободного члена уравнения регрессии и его коэффициента, основанное на геометрическом смысле этих величин, если рассматривать уравнение регрессии как уравнение прямой линии или линии регрессии. Смысл остальных столбцов понятен из их названия.

Кроме уже рассмотренных показателей точности уравнения регрессии обычно ещё используют коэффициент детерминации.

Коэффициент детерминации (R-квадрат) является удобной оценкой качества подгонки данных моделью. Выясним его смысл. В общем случае коэффициент детерминации определяется из соотношения

14

R2 = ,

т. е. это доля выборочной дисперсии переменной y, которая объясняется моделью. Следует иметь в виду, что также соответствует выборочному среднему (см. соотношение (1.2)). Следовательно, коэффициент детерминации характеризует долю вариации зависимой переменной, обусловленную вариацией независимой переменной. Обычно он выражается в процентах, поэтому, например, если R2 = 75%, то это значит, что 75% вариации зависимой переменной у объясняется вариацией независимой переменной х, а остальные 25% изменения у объясняются либо ошибками наблюдений, либо действием неучтенных факторов, либо тем и другим.

Известно, что если модель содержит свободный член, то справедливо соотношение (следует из ) () = 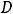( ) + (), откуда следует, что

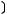= 1 – = 1 – .

Отсюда следует, что действительно определяет, какую долю выборочной вариации можно объяснить моделью.

Если уравнение регрессии содержит свободный член, то оба выражения для эквивалентны. Кроме того, в этом случае можно показать, что 0 все равны 0 и равен 1, если в уравнении регрессии содержится только константа).

Можно показать, что в случае парной линейной регрессии коэффициент детерминации равен квадрату коэффициента корреляции, т.е. R2 = .

Следует иметь в виду, что 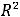измеряет только качество линейной аппроксимации, но не меру качества статистической модели. Кроме того, чувствителен к определению зависимой переменной и в случае её изменения разные модели по сравнивать нельзя.

1.3.Спецификация уравнения регрессии

Под спецификацией уравнения регрессии понимают выбор объясняющих переменных и установление вида связи между изучаемыми явлениями. В случае парной регрессии эта задача сводится к выбору независимой переменной и вида связи. Решение этих вопросов должна давать теория, описывающая взаимосвязи изучаемых процессов.

К ошибкам спецификации в случае парной регрессии можно отнести неправильный выбор доминирующего фактора, влияющего на изменение изучаемого показателя, или неправильный выбор вида зависимости между изучаемыми показателями. И в том и в другом случае будут нарушены

15

предпосылки МНК, особенно 3-я и 4-я, т.е. остатки регрессии будут гетероскедастичными и автокоррелироваными.

Гетероскедастичность и автокорреляция остатков уравнения регрессии могут сказаться на эффективности оценок, полученных на основе МНК и на смещённости оценки их дисперсии. Поэтому интервальные оценки и статистические выводы о значимости оценок в этом случае могут быть ненадёжными.

Разработаны специальные статистические методы проверки остатков на гомоскедастичность и автокорреляцию. Рассмотрим сначала наиболее простые из них.

1.3.1. Проверка остатков регрессии на гетероскедастичность (тест Голдфелда – Квандта)

Этот тест применяется в предположении нормально распределённых остатков и в предположении их пропорциональности величинам объясняющей переменной х. Для применения рассматриваемого теста пары наблюдений упорядочиваются в порядке роста значений независимой переменной х. Затем выбираются первые и последние наблюдения в количестве не менее n/3. По выбранным наблюдениям строятся уравнения регрессии (отдельно по каждому набору) и сравниваются их остаточные суммы квадратов. Гипотеза о гомоскедастичности в этом случае будет равносильна гипотезе о том, что остатки в этих уравнениях представляют собой выборочные наблюдения нормально распределённых случайных величин с одинаковыми дисперсиями. Сравнивая эти дисперсии по критерию Фишера (число степеней свободы числителя и знаменателя здесь совпадают, т. к. слева и справа берётся одинаковое число наблюдений) принимаем или отклоняем гипотезу о гомоскедастичности остатков.

Несмотря на ограниченность применения этого критерия (пропорциональность величин остатков значениям независимой переменной), данный тест работает с элементами выборки и не требует больших объёмов выборки как асимптотические тесты.

.

1.3.2. Проверка остатков регрессии на автокорреляцию (статистика Дарбина – Уотсона)

При анализе остатков на автокорреляцию в случае пространственной выборки надо меть в виду, что последовательную зависимость остатков друг от друга необходимо рассматривать не для случайного набора пар наблюдений, а для пар наблюдений, упорядоченных по величине значений независимой

16

проверяется гипотеза H0: = 0, т. е. что автокорреляция первого порядка отсутствует, так что если р-величина больше принятого уровня значимости, то гипотеза об отсутствии автокорреляции не отклоняется.

Как уже отмечалось, статистика Дарбина-Уотсона в большей мере используется при анализе временных рядов, поскольку именно для них актуально понятие автокорреляции. Однако она может быть использована для проверки правильной спецификации уравнения парной (простой) регрессии, но при этом необходимо случайную выборку упорядочить по степени возрастания независимой переменной. Тогда появится смысл в понятии «последовательные остатки». Если при этом с помощью критерия Дарбина-Уотсона обнаружена существенная автокорреляция остатков, то необходимо признать наличие проблемы в спецификации уравнения регрессии и либо вернуться к выбору объясняющей переменной, либо к форме регрессионной зависимости, либо попытаться избавиться от автокорреляции другими методами.

Следует иметь в виду, что статистика Дарбина-Уотсона обладает рядом недостатков: проверяет автокорреляцию только первого порядка, имеет области неопределённости и не может использоваться, если в качестве независимой переменной выступает лаговое значение зависимой переменной и если в уравнении регрессии отсутствует константа.

Несмотря на указанные недостатки, данная статистика используется наиболее часто и работает с выборочными наблюдениями, не требуя жёстких требований к выборке в отличие от асимптотических критериев.

Пример 1. Анализ функции потребления.

Приведём пример использования рассмотренных положений теории по простой регрессии, анализируя зависимость расхода 60 семей от их доходов. Эта информация представлена на графике (рисунок 1.1).

Рисунок 1.1 – График исходных данных

18

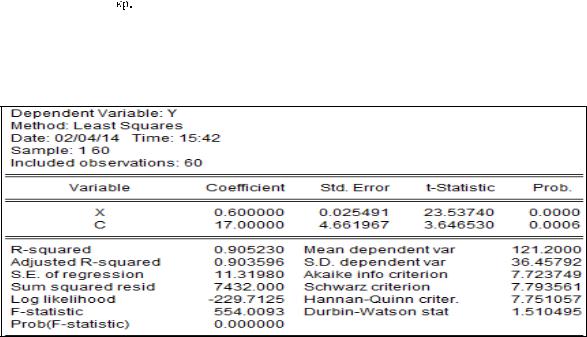
Уравнение регрессии зависимости расходов (y) от доходов (х) раcсчитано в EViews и отчёт о регрессии приведён ниже (рисунок 1.2).

Проанализируем его. В отчёте указан метод оценивания параметров уравнения регрессии (Least Squares – наименьшие квадраты), число наблюдений

– 60. В столбце «коэффициенты» указаны оценки параметров уравнения регрессии (коэффициент при х равен 0,6 и свободный член (с) равен 17). Следовательно, можно выписать уравнение регрессии: = 17 + 0,6х. За столбцом «коэффициенты» следуют столбцы стандартных ошибок и t-статистик. Последний столбец (Prob.) – это расчётный уровень значимости, т.е. вероятность того, что |t |≤ . Если эта вероятность меньше (по умолчанию будем в дальнейшем принимать = 0,05), то соответствующая оценка значимо отлична от нуля. У нас обе вероятности меньше 0,05, следовательно, обе оценки значимо отличны от нуля.

Рисунок 1.2 – Отчёт о регрессии

Проанализируем показатели точности уравнения регрессии. Начнём с анализа значимости уравнения регрессии. F-satstistic = 544, а вероятность для неё (Prob(F-statistic)) равна нулю. Это – результат дисперсионного анализа уравнения регрессии. Здесь проверяется гипотеза о значимости уравнения регрессии, т. е., что коэффициент уравнения регрессии равен нулю. Поскольку расчётный уровень значимости здесь меньше принятого (0,05), то гипотеза о равенстве коэффициента регрессии отклоняется и считается, что уравнение регрессии значимо.

Коэффициент детерминации (R-squared) равен 0,9. Следовательно, изменение расходов в нашем примере на 90% зависит от изменения доходов. Показатель Adjusted R-squared (исправленный коэффициент детерминации) в простой регрессии не анализируется. Затем указана стандартная ошибка регрессии (S.E.

19

подробном анализе (см. далее в примере).

Далее (в правом столбце нижней части отчёта) указано среднее значение зависимой переменной (Mean dependent var) – средний уровень доходов этих 60 семей (он равен 121,2). Стандартную ошибку регрессии (11,32) можно сравнить с этим средним доходом и определить, насколько точно в среднем прогнозируются расходы семьи по этому уравнению регрессии.

Далее указаны три информационных критерия (Akaike, Schwarz, Hannan), которые в парной регрессии не анализируются.

Статистика Дарбина – Уотсона (d) рассчитана для проверки гипотезы о наличии в остатках регрессии автокорреляции первого порядка. Как отмечалось, эта информация более полезна при анализе временных рядов. Для пространственной информации надо данные упорядочить, чтобы понятие «соседние» остатки приняло какой-то смысл. В случае случайной выборки это понятие теряет смысл. В нашем случае данные упорядочены по росту доходов (см. рисунок1.1), следовательно, можно анализировать эту статистику без предварительного упорядочения. Как видно из отчёта, d = 1,51. Табличные значения нижней (dl) и верхней (du) границ соответственно равны 1,55 и 1,62. Построим области принятия решения о наличия или отсутствия автокорреляции в остатках в соответствии с приведённой схемой в таблице 1.3.

Как видим, расчётное значение попало в область, где автокорреляция есть. Да и по графику (рисунок 1.3) видно, что остатки не являются случайным процессом. Видна закономерность их изменения – регулярная смена отрицательных остатков на положительные. На этом рисунке изображены реальные (Actual) и расчётные (Fitted – подобранные) значения моделируемой переменной (расходов) и остатки (Residual). Причём, правая вертикальная ось – для моделируемого показателя, левая – для остатков.

20