Кроме близости соответствующих характеристик линейной и степенной производственных функций на эквивалентность указанных производственных функций указывает также и близость в экспериментальных расчетах соответствующих коэффициентов детерминации.
Различие характеристик линейной и степенной производственных функций обусловлено разными гипотезами относительно постоянства параметров указанных производственных функций. Так, если в линейной производственной функции (1.20) постоянными предполагаются предельные эффективности факторов a и b, то в степенной производственной функции (1.21)
– факторные коэффициенты эластичности выпуска и .
1.2.3. Исследование свойств и характеристик статических производственных функций
Характеристики и свойства статических производственных функций исследуем на примере полученной ранее макроэкономической степенной производственной функции экономики США периода 1950 – 1960 гг.:
Y=1,978·K , ·L ,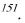
Воспользовавшись оценками макроэкономической степенной производственной функции экономики США периода 1950 – 1960 гг.
ln(А) = 0,682, = 0,849, =0,151
и показателями производственных факторов (первого года анализируемого периода) K1950=310,42 млрд долл. и L1950 = 125,12 млрд ч, необходимо исследовать свойства и характеристики статической степенной производственной функции:
48
I.Расчет продукции Y1950 по формуле
Y1950 = A .K1950 .L1950 .
II.Исследование эффективности производственных факторов:
Средние и предельные эффективности производственных факторов K и L и их экономический смысл.
Соотношение между средней и предельной эффективностью производственных факторов.
Коэффициенты эластичности выпуска по производственным факторам K и L в степенных производственных функциях и их экономический смысл.
III. Проверка выполнения трех предположений о свойствах
производственной функции Y=F(K,L) (1.1)-(1.3):
F(0, L) = 0 , F(K, 0) = 0 ;
|
F( K ,L ) |
0, |
|
F( K ,L ) |
0 |
||
|
|
|
|
|
|||
|
|
K |
L |
||||
|
|
|
|
|
при K>0, L>0; |
||
|
2 F |
0, |
|
2 F |
|
0 |
|
|
K 2 |
|
L2 |
|
|||
|
|
|
при K>0, L>0; |
||||
IV. Исследование отдачи от расширения масштабов производства
Однородность производственных функций.
Эластичность производства.
Теорема Эйлера.
49
Соотношение между эластичностью производства и частными эластичностями выпуска относительно изменения затрат производственных факторов.
Соотношение между эластичностью производства и показателем степени однородности степенной производственной функции.
Математическая и экономическая интерпретация четвертого предположения об однородности степенной производственной функции.
V.Исследование взаимного замещения производственных факторов
o Экономический смысл взаимного замещения производственных факторов.
o Изокванты их свойства.
o Построение изокванты степенной производственной функции постоянного выпуска Y=Y0.
o Предельная норма замещения производственных факторов в рамках:
а) произвольной производственной функции;
б) степенной производственной функции.
o Изоклинали степенной производственной функции.
o Эластичность замещения производственных факторов.
o Доказательство равенства единице эластичности замещения производственных факторов в рамках степенной производственной функции.
50
Перейдем к исследованию свойств и характеристик статической степенной производственной функции:
I.Расчет продукции Y1950
Подставив известные значения параметров A, ,
и производственных факторов K1950, L1950 в степенную производственную функцию Yt = A .Kt .Lt , получим расчетное значение величины ВНП США для 1950 г.
Y1950=1,978. (310,42)0,849. (125,12)0,151=535,2 млрд долл.
II.Исследование эффективности производственных факторов
Средние и предельные эффективности производственных факторов K и L и их экономический смысл.
При исследовании эффективности производственных факторов можно воспользоваться формулами (1.33) – (1.36) расчета средних производительностей AyK и AyL и предельных производительностей MyK и MyL факторов K и L, подставив соответствующие значения параметров и факторов (для первого года анализируемого периода) 1950 года:
AyK = |
|
Y |
|
= |
|
|
|
F( K ,L ) |
= |
|
A |
K |
L |
|
= A·K |
·L ; |
||||||||||||||||
|
K |
|
|
|
|
|
|
K |
|
|
|
|
K |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
AyL = |
Y |
|
|
= |
|
|
F( K ,L ) |
= |
|
|
A |
K |
L |
= A·K ·L |
|
|
|
|||||||||||||||
|
L |
|
|
|
|
|
|
|
L |
|
|
|
|
|
L |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
MyK= |
|
|
Y |
|
= |
|
|
F( K ,L ) |
= |
|
A K 1 L |
|
Y |
; |
||||||||||||||||||
|
|
K |
|
|
|
K |
|
|
|
|
|
K |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
My = |
|
|
Y |
= |
|
|
|
|
F( K ,L ) |
= |
|
|
Y |
. |
|
|
|
|
|
|
||||||||||||
L |
|
|
L |
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
51
После расчета средних производительностей AyK и AyL и предельных производительностей MyK и MyL производственных факторов K и L рассмотреть их экономический смысл.
Соотношение между средней и предельной эффективностью производственных факторов.
Подставив найденные значения средних и предельных производительностей в соотношения
MyK ≤ 1 (MyK ≤ AyK), AyK
и
MyL ≤ 1 (MyL ≤ AyL), AyL
убедиться в справедливости для степенных производственных функций утверждений, что предельные продукты производственных факторов всегда меньше соответствующих средних продуктов производственных факторов.
Коэффициенты эластичности выпуска по факторам K и L в степенных производственных функциях и их экономический смысл.
Для расчета коэффициентов эластичности выпуска по производственным факторам K и L в степенных ПФ воспользуемся формулами (1.39)-(1.40)
EK |
Y |
|
|
|
Y |
|
|
Y |
|
K |
MyK |
= ; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
K |
|
|
|
K |
|
|
K |
|
Y AyK |
|||||
E |
|
|
Y |
|
|
L |
|
|
MyL |
= . |
|
|
|||||
L |
L |
|
Y |
|
|
|
|
||||||||||
|
|
|
AyL |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
После расчета коэффициентов эластичности выпуска по факторам K и L в степенных производственных функциях рассмотреть их экономический смысл.
III. Проверка выполнения трех предположений о свойствах
52
производственной функции Y=F(K,L) (1.1) – (1.3):
F(0, L) = 0 , F(K, 0) = 0 ;
|
F( K ,L ) |
0, |
|
F( K ,L ) |
0 |
при K>0, L>0; |
||||
|
|
|
|
|
|
|
|
|||
|
|
K |
|
L |
||||||
|
|
|
|
|
|
|
||||
|
2 F |
0, |
|
2 F |
|
0 |
при K>0, L>0. |
|||
|
K 2 |
|
L2 |
|||||||
|
|
|
|
|
|
|
|
|||
Проверка первых двух предположений не представляет сложностей. Рассмотрим проверку третьего предположения. Формулы для расчета вторых частных производных имеют вид:
2Y |
( |
1 ) |
A K 2 L |
( 1 ) |
Y |
; |
|||
K 2 |
K 2 |
||||||||
|
|
|
|
|
|
||||
2Y |
( |
1 ) |
Y |
|
|
|
|||
|
|
|
. |
|
|
|
|||
2 |
|
2 |
|
|
|
||||
L |
|
|
L |
|
|
|
|||
Подставив известные значения параметров и производственных факторов в полученные соотношения, легко проверить справедливость третьего предположения.
IV. Исследование отдачи от расширения масштабов производства
Однородность производственных функциях.
Производственная функция F(K,L) называется однородной функцией степени , если для произвольных значений K, L и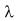
она удовлетворяет соотношению
F( K, L) =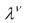
F(K,L) .
Однородность производственной функции означает, что при увеличении
53
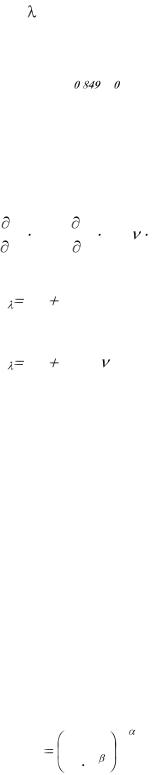
затрат производственных факторов в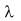
раз объем производства возрастает в среднем в v раз.
Определите степень однородности производственной функции:
Y=1,978·K , ·L ,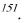
Для выполнения остальных пунктов этого раздела воспользуйтесь формулами (1.14) – (1.16):
|
Y |
K + |
|
Y |
L = F(K, L); |
|
K |
|
L |
||
|
|
|
|
||
E |
EK |
EL; |
|
||
E |
EK |
EL = . |
|||
V. Исследование взаимного замещения производственных факторов
Возможность |
взаимного замещения ресурсов |
означает, что |
одно и |
||
то же количество |
продукта Y0 может быть произведено при различных |
||||
сочетаниях |
ресурсов. |
Изокванта — геометрическое |
поле точек, |
которым |
|
соответствует одинаковый уровень выпуска продукции. |
|
|
|||
Для |
степенной |
производственной функции линии постоянного уровня |
|||
выпуска Y=Y0 образуют семейство изоквант, уравнение которых можно получить из уравнения степенной производственной функции, принимая, например, K как функцию L:
|
Y0 |
1 / |
|
K( L ) |
(1.64) |
||
A L |
|||
|
|
54