
- •Хабаровск 1999
- •III. ПОСЛЕДОВАТЕЛЬНОСТИ В ЭКОНОМИЧЕСКИХ ЗАДАЧАХ
- •3.1. Задачи о непрерывном начислении процентов
- •ЗАДАЧИ
- •4.7. Метод наименьших квадратов
- •Результаты вспомогательных вычислений для получения коэффициентов системы нормальных уравнений (4) располагаем в таблице:
- •Характеристическое уравнение имеет вид
- •Тогда суммарная производительность (за рабочий день) будет:
- •ЗАДАЧИ
- •Тогда прибыль от реализации готовой продукции имеет вид :
- •ОГЛАВЛЕНИЕ
- •Сборник задач

Предположим, |
|
что |
|
существуют |
lim an a, |
lim Cn |
C |
и |
lim Pn |
P , |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
тогда, переходя в последнем уравнении к пределу при n |
, |
|||||||||||||||||||||||||||||||||||
получим lim (an |
|
bPn ) |
|
lim (Cn 1 |
dPn 1) |
или |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a - bP = C + dP. Отсюда найдем |
|
|
a |
c |
|
lim an |
lim cn |
. Можно |
||||||||||||||||||||||||||||
Р= d |
b |
|
n |
d |
b |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
||||
показать, |
что если |
d |
|
|
1 и существуют |
lim a , |
lim c |
, то существует и |
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
n |
n |
n |
|
n |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
lim Pn |
|
a |
c |
P. |
В этом случае Р называется предельным значением |
|||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
d |
b |
||||||||||||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
равновесных цен Рn. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Пример. |
|
Найти предельное значение равновесных цен в |
|||||||||||||||||||||||||||||||||
паутинообразной |
|
|
|
|
|
|
|
|
модели |
|
|
|
|
рынка, |
|
|
|
|
если |
|||||||||||||||||
a |
n |
1 |
|
, c |
|
|
|
n |
|
, |
|
b |
1,5, |
d |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
n |
1 |
|
n |
|
|
2n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Решение. |
|
Найдем lim |
n |
1 |
|
1 |
a |
и |
c |
lim |
|
n |
|
1 |
, |
т.к. |
d |
1 |
|||||||||||||||||
|
|
n |
2 |
|
2n 1 |
2 |
b |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
и а, с |
определены, то |
|
Р – предельное значение равновесных цен |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
c |
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
определено Р= |
|
|
|
2 |
|
|
0,2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
b |
d |
|
|
|
1,5 |
1 |
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ЗАДАЧИ
1.Годовая процентная ставка р=24%. Рассчитать величину вклада
через 5 лет, если начальный вклад Q0=2000 руб., а проценты начисляются ежеквартально. Вычислить величину вклада через 5 лет при непрерывном начислении процентов.
2.За два года величина вклада выросла в 1,4641 раза при начислении процентов раз в полгода. Во сколько раз возросла бы величина вклада при непрерывном начислении процентов?
3. |
Норма амортизации |
равна 10%. Найти остаточную стоимость |
||||||||||||
|
основного капитала на начало 3-го года и его предельную |
|||||||||||||
|
стоимость, если инвестиции в n-ый год In= |
0,2n 1 |
у.е. и начальное |
|||||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
3 |
|
|
|
значение k0=2у.е. |
|
|
|
|
|
|
|
|
|
|
|
||
4. |
Ежегодные |
инвестиции |
в |
основной |
капитал |
определяются |
||||||||
|
равенством |
In= |
n |
1 |
|
у.е. |
Определить |
предельную |
||||||
|
|
|
|
|||||||||||
|
0,1n2 |
2n |
1,9 |
|||||||||||
|
стоимость и начальную стоимость основного капитала, если |
|||||||||||||
|
норма амортизации =5% и величина основного капитала на |
|||||||||||||
|
начало второго года k1=2,4 у.е. |
|
|
|
|
|
|
|
||||||
5. |
Пусть спрос на некоторый товар в момент времени n |
|||||||||||||
|
определяется равенством QД(n) = |
n2 |
n |
1 |
|
0,4P , а предложение |
||||||||
|
2n2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
n |
1 |
n |
|
||||

Q |
(n)= |
n |
2 |
0,2P |
, где Р – равновесная цена в момент времени |
|
|
|
|||||
S |
|
3n |
1 |
n 1 |
n |
|
|
|
|
|
|||
n t. Определить значение равновесной цены Р3 и предельное значение равновесных цен Р, если начальная цена Р0=0,5.
t. Определить значение равновесной цены Р3 и предельное значение равновесных цен Р, если начальная цена Р0=0,5.
6.Пусть Рn – значение равновесной цены в момент времени n t. Определить Р3 и предельное значение равновесных цен Р, если начальная цена Р0=1, а объемы спроса QД(n) и предложения QS(n)
t. Определить Р3 и предельное значение равновесных цен Р, если начальная цена Р0=1, а объемы спроса QД(n) и предложения QS(n)
определяются |
равенствами |
QД(n)= |
2n2 |
n |
2 |
1,2 P ; |
||||
n2 |
|
|
||||||||
|
|
|
|
|
|
|
n |
1 |
n |
|
QS(n)= |
n2 |
n |
1 |
0,8P |
. |
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|||
|
n |
2 |
n 1 |
|
|
|
|
|
|
|
IV. ПРОИЗВОДНАЯ. ПРЕДЕЛЬНЫЙ АНАЛИЗ
4.1. Экономический смысл производной
1.Пусть y=f(x) определена на промежутке X. Возьмем точку х X . Дадим значению х приращение х 0 , тогда функция получит приращение у=f(x+ х)-f(x).
Производной функции y=f(x) называется предел отношения приращения функции к приращению аргумента при стремлении
последнего к нулю (если этот предел существует ) :
y |
lim |
y |
lim |
f (x x) |
f (x) |
||
x |
x |
|
|
||||
|
x |
0 |
x 0 |
|
|
||
|
|
|
|
|
|||
Производная функции |
y |
x |
|
характеризует |
мгновенный прирост |
||
или скорость изменения зависимости переменной y (функции f(x)) в точке x.
ПРИМЕР 1. Стоимость определенной продукции на 1 рубль основных производственных фондов (фондоотдача) y зависит от
коэффициента |
сменности |
оборудования |
х |
(характеризующего |
||||||
степень равномерности использования |
оборудования по сменам) |
|||||||||
|
|
|
|
|||||||
следующим образом: y= x +c, где |
c – постоянная величина. Найти: |
|||||||||
а) скорость |
изменения |
фондоотдачи |
при |
коэффициенте |
||||||
сменности оборудования x=1,35; |
|
|
|
|
|
|
||||
б) найти функцию этого изменения, |
если |
c |
= |
0, |
полагая, что |
|||||
некоторое |
время фондоотдача |
будет меняться |
с |
постоянной |
||||||
скоростью. |
|
|
|
|
|
|
|
|
|
|

Решение: |
а) |
скорость |
изменения |
фондоотдачи определяется |
||||||||||
производной |
y |
|
|
1 |
|
, |
при x=1,35 |
y=(1,35) = |
1 |
|
0,43, |
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
2 |
|
x |
2 1,35 |
|||||||||||
т.е. при изменении коэффициента |
сменности |
на единицу |
||||||||||||
фондоотдача увеличивается |
приближенно на 0,43 руб.; |
|
|
|||||||||||
б) фондоотдача |
|
y |
|
будет меняться |
с постоянной скоростью |
|||||||||
v= y (1,35) = 0,43 в случае линейной зависимости ,т.е. по касательной к кривой в точке x0=1,35 ; уравнение касательной имеет вид: y – 1,16 = 0,43 (x-1,35), где
y(1,35)=1,16. После преобразования имеем уравнение фондоотдачи y=0,43x+0,58.
Пусть функция u = u (t) выражает количество произведенной
продукции u |
за |
время t |
. |
Необходимо найти производительность |
|||||||||||||
труда |
в момент t0.За период времени от t0 до t0+ t |
количество |
|||||||||||||||
произведенной |
продукции |
изменяется |
на |
|
величину |
u u(t 0 |
|||||||||||
+ t) |
u(t 0). Тогда средняя производительность труда |
за время t |
|||||||||||||||
будет равна |
отношению |
|
ср= |
u |
. |
Определим производительность |
|||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
труда |
в момент |
времени |
|
t0 |
как |
предельное |
|
|
значение |
средней |
|||||||
производительности |
u |
при |
t |
0 ,т.е. |
lim |
|
u |
|
|
||||||||
|
|
|
|
|
|
|
|||||||||||
t |
|
t |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
t |
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, производительность труда есть производная объема произведенной продукции по времени.
Темпом изменения функции называется величина
Т y |
= |
y (x) |
(ln y) |
|
y |
||||
|
|
|
Пример 2. Производительность труда бригады рабочих может быть описана уравнением y = -2,5t2 + 15t + 100, 1 t 8 - рабочее время в часах. Вычислить скорость и темп изменения производительности труда при t = 2, t = 7.
|
|
Решение. Скорость изменения производительности труда |
||||
выражается производной: |
|
|
||||
|
|
|
y = -5t + 15 |
y (2) = 5 ед/ч |
y (7) = -20 ед/ч. |
|
Темп |
|
изменения |
(относительная |
скорость |
изменения) |
|
производительности |
труда |
выражается |
формулой |
|||
Ty= |
y |
|
5t 15 |
|
|
|
y |
|
2,5t 15t 100 |
|
|
|
|
|
|
|
|
|
||
Ty (t =2) = 1/24 (ед/ч) Ty(t=7) = -8/33(ед/ч)
Знаки плюс и минус показывают, что в начале смены наблюдалось увеличение производительности, а в конце – снижение.

Рассмотрим еще одно понятие, иллюстрирующее экономический смысл производной.
Пусть К=К(х) функция издержек производства, где х-объем выпускаемой продукции, пусть 
соответствовать
y |
y(x x) y(x) приращение издержек производства. Величина |
|
y |
- |
|
x |
||
|
есть среднее приращение производства на единицу продукции.
Найдем предельные издержки lim |
y |
K (x). |
|
|
|||
x |
|||
x o |
|
К x
x характеризует приближенно дополнительные затраты на производство дополнительной единицы продукции .
характеризует приближенно дополнительные затраты на производство дополнительной единицы продукции .
Предельные издержки зависят от уровня производства (количества выпускаемой продукции) х и определяются не постоянными производственными затратами , а лишь переменными (на сырье, топливо, электроэнергию, и т.п.). Аналогично могут быть определены, предельная выручка, предельный доход, предельный продукт, предельная полезность и другие предельные величины.
Предельные |
величины |
характеризуют |
не |
состояние |
(как |
суммарная или |
средняя |
величина ), |
а |
процесс изменения |
|
экономического объекта. Таким образом, производная выступает как скорость изменения некоторого экономического процесса по времени или относительно другого исследуемого фактора.
Пример 3. Пусть К(х)=50х-0,05х3 (ден.ед.) функция издержек производства. Определить средние и предельные издержки, если объем составляет 10 условных единиц.
|
|
|
К х |
|
50x 0,05x3 |
||
Средние издержки |
|
|
|
50 0,05x2 |
|||
|
|
||||||
|
|
|
х |
|
x |
||
при х=10 |
К 10 |
= 45 (ден.ед.) |
|||||
10 |
|||||||
|
|
|
|
|
|
||
Предельные издержки К |
х =50-0,15х2 |
||||||
К х =50-0,15 |
102 = 35 (ден. ед.). |
||||||
Итак, если средние издержки на производство единицы продукции составляют 45 ден. ед, то предельные издержки, т.е. дополнительные затраты на производство дополнительной единицы продукции при данном уровне производства (объеме выпускаемой продукции 10 ед), составляют 35 ден.ед.

4.2. Эластичность функции. Свойства эластичности
Для исследования экономических процессов и решения других прик-ладных задач часто используется понятие эластичности функции.
Эластичностью функции EX (у) называется предел отношения относительного приращения функции у к относительному приращению
аргумента х при x 0
Ех (y)= lim ( |
y |
: |
x |
) |
x |
lim |
y |
|
x |
y . |
y |
|
y |
x |
|
y |
|||||
x 0 |
|
x |
x 0 |
|
|
|||||
Эластичность функции показывает приближенно, на сколько процентов изменится функция у= f(x) при изменении
независимой переменной х на 1%. |
|
|
|
1. Эластичность функции равна произведению |
независимой |
||
перемен- |
|
|
|
ной х на темп изменения функции Ту = (ln y) |
y |
, т.е. |
|
|
|||
y |
|||
|
|
||
Ех(у)=х Ту |
|
|
|
2. Эластичность произведения (частного) двух функций равна сумме (разности) эластичностей этих функций
Ex (u v) = Ex (u) + Ex (v)
v) = Ex (u) + Ex (v)
Ex |
u |
= Ex (u)-Ex (v) |
|
v |
|||
|
|
Если Ex ( y) >1, то изменению переменной х на 1%
соответствует изменение функции более чем на 1%, то говорят, что функция
эластична относительно х.
Если |
|
Ex ( y) |
|
1, то функция нейтральна, т.е. изменение х на 1% |
|
|
|||
приводит к изменению y(х) на 1%. |
||||
Если |
|
Ex ( y) |
|
<1, функция неэластична, при изменении х на 1% |
|
|
|||
функция у(х) изменяется менее чем на 1%.
Пример 3 (Эластичность спроса относительно цены). Пусть функция спроса на некоторый вид товара имеет вид q 2e 2 p , где p- цена товара (ден.ед). Определить эластичность спроса при цене товара p=3 (ден.ед)
E |
|
(q) |
p |
q |
p |
(2e 2 p ) |
2 p . |
|
p |
q |
2e |
2 p |
|||||
|
|
|
|
|
|
|
||

Ep 3 (q) 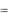 2
2  3
3  6. Это означает, что при цене 3(ден.ед)
6. Это означает, что при цене 3(ден.ед)
повышение цены на 1% вызовет снижение спроса на 6%, т.е спрос эластичен.
Пример 4. (Эластичность спроса относительно дохода). Пусть спрос на данный товар в зависимости от дохода потребителей выражается формулой q = 
 r , где r – доход. Тогда эластичность
r , где r – доход. Тогда эластичность
спроса относительно дохода есть Er(q)= |
r |
|
dq |
|
r |
|
1 |
|
|
r |
|
1 |
0,5. |
|
q |
|
dr |
|
|
|
|
|
|
|
2r |
2 |
|||
|
|
|
r |
|
2 r |
|
||||||||
|
|
|
|
|
|
|
||||||||
Это означает, что повышение дохода потребителей на 1% вызовет повышение спроса на товар на 0,5%.
Пример 5 (Эластичность предложения относительно цены). S = S(p) – есть функция предложения (товара, труда, услуг) в
зависимости |
от |
цены |
р, |
тогда |
Ep |
(s)= |
p |
|
ds |
|
называется |
|||||||||
s |
|
dp |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
эластичностью предложения от цены. |
|
|
|
|
|
|
|
|||||||||||||
|
|
3 |
(4 |
p2 ) |
|
|
|
|
|
|
|
|
|
|
|
|||||
Пусть S(p) = |
|
|
|
|
|
|
. Найти эластичность предложения при цене |
|||||||||||||
|
|
1 |
|
8 p |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
товара |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р = 4 (ден.ед.). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ep(s)= |
p (1 |
8 p) |
|
|
3 |
(4 |
|
p2 ) |
|
2 p ( p |
4 p2 |
16) |
. При р = 4 |
Ер(s) = 0,7, |
||||||
3 (4 |
p2 ) |
|
|
1 |
8 p |
(4 |
p2 ) |
(1 |
8 p) |
|||||||||||
т.е. прирост предложения, соответствующий увеличению цены р = 4 (ден.ед.) на 1% составляет 0,7%.
4.3. Экстремум функции
Пусть на промежутке Х задана функция у=f(x).
Необходимое условие экстремума. Для того чтобы функция у=f(x) имела экстремум в точке х0 X, необходимо , чтобы ее
производная в этой точке равнялась нулю ( у (х0 ) 0) или не |
существовала. |
Первое достаточное условие экстремума . Если при переходе через точку х0 производная дифференцируемой функции у=f(x) меняет свой знак с плюса на минус, то точка х0 есть точка максимума функции у=f(x), а если с минуса на плюс, то х0 – точка минимума.

Второе достаточное условие экстремума. Если производная
f (x) |
дважды дифференцируемой функции равна нулю в |
|
некоторой точке |
||
x0 |
X ,а |
производная f (x0 ) положительна, то х0 есть точка |
минимума |
функции f (x) ,если f (x0 ) отрицательна,то х0 точка |
|
максимума.
Пример. Производитель реализует свою продукцию по цене р=150(ден.ед) за единицу, а издержки при этом задаются кубической
зависимостью S(x)=6x+3x3. Найти оптимальный объем выпуска продукции и соответствующую ему прибыль.
Решение. Пусть объем выпускаемой продукции х . Составим функцию прибыли.C(x)=150x-(6x+3x3), где рх - доход от реализуемой продукции.
1.Найдем C (x) 150 (6 9x2 ) 144 9x2 .
2. Найдем критические точки.
C (x) 144 9x2 0 |
х1 = 4 |
х2 = -4 – не рассматриваем по смыслу задачи. 3. Найдем C (x)
(x)  18x и определим знак второй производной при х=4
18x и определим знак второй производной при х=4
C (4)
(4)  72 0 , следовательно, при х=4 прибыль С(х) максимальна.
72 0 , следовательно, при х=4 прибыль С(х) максимальна.
4. Находим максимум функции.
Сmax(x=4)=150 4 (6
4 (6  4 3
4 3  64) 384 (ден.ед)
64) 384 (ден.ед)
Пример. Капитал в 1 млрд рублей может быть размещен в банке под 50% годовых или инвестирован в производство, причем эффективность вложения ожидается в размере 100%, а издержки
задаются квадратичной зависимостью. Прибыль облагается налогом в р%. При каких значениях р вложение в производство является более эффективным, нежели чистое размещение капитала в банке?
Решение. Пусть х (млрд руб.) инвестируется в производство, а
(1-х)-

размещается под проценты. Тогда размещенный капитал станет равным
(1 |
x)(1 |
50 |
) |
|
|
3 |
|
|
|
3 |
x , |
|
|
а капитал, вложенный в производство, |
|
|||||||||||||||||||||||||||||||||||||||
100 |
2 |
|
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x(1 |
|
100 |
) |
|
2x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Издержки составят a х2, |
т.е. |
прибыль от вложения в |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
производство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примечание [Рита1]: |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
С=2х- a х2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Налоги составят (2х- a х2) |
|
|
p |
, т.е. чистая прибыль окажется |
||||||||||||||||||||||||||||||||||||||||||||||||||
100 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
равной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
(1 |
|
|
|
|
p |
|
)(2x |
|
ax2 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Общая сумма через год составит: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
A(x) |
3 |
|
|
3 |
x |
(1 |
|
|
|
p |
|
)(2x |
ax2 ) |
|
3 |
|
2(1 |
|
|
|
|
|
p |
) |
|
3 |
x a(1 |
|
p |
)x2 |
, |
|||||||||||||||||||||||
2 |
|
|
2 |
|
100 |
2 |
|
100 |
2 |
100 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
и требуется найти максимальное значение этой функции на |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
отрезке |
0;1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Имеем |
|
|
A (x) |
2(1 |
|
|
|
|
p |
) |
|
3 |
|
|
2a(1 |
|
|
|
p |
|
|
)x и |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
100 |
2 |
|
100 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2(1 |
|
|
p |
) |
|
3 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
A (x) |
0 , |
при |
|
|
x |
100 |
2 |
, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a(1 |
|
|
) |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
A (x) |
|
2a(1 |
|
|
p |
) |
|
|
|
|
0 , |
|
|
|
т.е., |
|
согласно второму достаточному |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
условию экс- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
тремума, |
х0 - точка максимума. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
Чтобы х0 |
принадлежало отрезку [0;1], |
необходимо выполнение |
|||||||||||||||||||||||||||||||||||||||||||||||||||
условия 0<2 (1- |
|
p |
) |
|
|
3 |
|
1 |
|
|
или р<25. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
100 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Таким образом, если р>25, то выгоднее ничего не вкладывать в производство и разместить весь капитал в банк. Если р<25 , то можно показать, что при х=хо
|
|
|
2 1 |
|
|
p |
3 |
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A(x0 )= |
3 |
+ |
100 |
|
|
2 |
|
|
3 |
A(0), |
||||
|
|
|
||||||||||||
2 |
4a 1 |
|
|
p |
|
|
2 |
|||||||
|
|
|
|
|
|
|||||||||
|
|
|
100 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||

т.е. вложение в производство является более выгодным, чем чистое размещение под проценты.
4.4. Определение оптимального размера партии
Пример: Пусть С1 – затраты на хранение одного изделия в единицу времени; С2 – общие затраты на производство одной партии;
n - число изделий в партии;
Т – продолжительность производства одной
партии.
Требуется определить размер партии n,при котором обработка N изделий (N>n) за время t потребует минимальных затрат.
Решение: Составим функцию у=f(х), выражающую зависимость суммарных затрат у от размера n.
Общее число партий Nn , тогда общие затраты на производство составят
C2 Nn . При определении затрат на хранение будем исходить из того,
что партия изделий по мере изготовления поступает на хранение и поэтому
за период ее изготовления Т хранится в среднем n2 изделий. Таким образом, затраты на хранение одной партии составляет С1 n2 T .
Суммарные
|
|
n |
N |
|
C1TN |
||
затраты на хранение составят |
C1 |
|
T |
|
|
|
. |
2 |
n |
2 |
|||||
Суммарные затраты на производство и хранение будут составлять.
y C |
N |
|
C1 |
TN . |
|
|
|
|
|
|
|
|
|
|
|
||
2 |
n |
2 |
|
|
|
|
|
|
Величины n и T взаимозависимые,очевидно, что |
t |
|
N |
NT nt |
||||
T |
|
n |
||||||
|
|
|
|
|
|
|
||

Подставляя в функцию y, получим y |
C2 N |
|
C1t |
n . |
|
n |
2 |
||||
|
|
||||
Исследуем функцию у=f(n) на минимум (С1, С2, N и t – заданные величины).
|
|
|
y |
C2 N |
|
C1t |
, |
|
|
|||||||||
|
|
|
n 2 |
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
y 0 , |
|
C2 N |
|
|
|
|
C1t |
0 |
, |
||||||
|
|
|
|
|
n 2 |
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
n |
|
|
2N |
|
C2 |
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
0 |
|
|
t C1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
y |
2C2 N |
0 |
, при найденном n0 |
функция достигает минимума. |
||||||||||||||
n3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Итак, оптимальным размером партии, минимизирующим суммарные за-
траты, будет |
n |
|
2NC2 |
|
. |
|
|||||
|
0 |
|
t C1 |
||
|
|
|
|||
Пример. Оптимальный размер капиталовложений.
Пусть планируется строительство и эксплуатация некоторого объекта, срок эксплуатации Т лет. Первоначальные капиталовложения составляют
К руб., а последующее ежегодные эксплуатационные расходы х руб. Пред-положим, что первоначальные капиталовложения зависят от последующих ежегодных расходов К=f (х).
Определить оптимальный размер первоначальных капиталовложений, при котором суммарные расходы достигают минимума. Решение.
Суммарные расходы по строительству и эксплуатации данного объекта за Т лет составят
|
y |
K |
x T |
f (x) |
xT. |
Исследуем |
функцию на минимум |
|
|
||
|
y |
K |
T |
f x |
T , |
y 0 , K T |
0 , K T из уравнения следует, что K <0, т.е. |
||||
начальные вложения убывают с ростом ежегодных эксплуатационных расходов.
Если K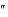 >0, то кривая К=f(х) вогнутая, т.е. если с ростом годовых эксплуатационных расходов, уменьшение начальных капиталовложений происходит с замедлением,то найденное значение х* из уравнения.
>0, то кривая К=f(х) вогнутая, т.е. если с ростом годовых эксплуатационных расходов, уменьшение начальных капиталовложений происходит с замедлением,то найденное значение х* из уравнения.

K
 T , определяет минимальные суммарные затраты. y*min =f(x )+x*T
T , определяет минимальные суммарные затраты. y*min =f(x )+x*T
4.5. Функция двух переменных
Пусть имеются две переменных х и у, и каждому набору их значений (х, у) из некоторого множества U соответствует одно вполне определенное значение переменной величины Z. Тогда говорят, что
задана функция двух переменных Z=f(x, у).
Дадим аргументу х приращение х, аргументу у –
приращение |
у. |
Величина |
Z f (x x, y y) f (x, y) называется полным |
приращением функции в точке (х,у).
Если задать только приращение аргумента х или аргумента у,
то полученные приращения функции соответственно
xZ=f(x+ x,y)-f(x,y), и y Z= f(x,y+ y)-f(x,y)
называются частными.
Частной призводной функцией z=f(x,y) по независимой переменной х называется функция переменных х и у, получающаяся при диффе-ренцировании f(x, y) по x в предложении, что у считается постоянной.
Zx |
z |
fx |
(x, y) lim |
x z |
|
x |
x |
||||
|
|
x 0 |
|||
|
|
|
|
Аналогично частной производной по у будет
Z |
z |
f y (x, y) lim |
y z |
. |
|
y |
y |
||||
|
y 0 |
|
|||
|
|
|
|
Частная производная по переменной х в точке (х,у) характеризует скорость изменения или прирост переменной Z при изменении х и постоянном значении у.
Коэффициентами частной эластичности Ex(z), Ey(z) называются величины
Ex (z) |
x |
Z x , E y (z) |
y |
Z y . |
|
2 |
2 |
||||
|
|
|
|||
Коэффициент частной эластичности Ex(z) |
приблизительно |
||||
показывает, |
|
|
|
|
|
на сколько процентов изменится функция при изменении переменной x
на 1% при неизменном значении у.
Пример. Функции спроса на товары А и В имеют вид:

х = 1000 - 20 р1 + р2 + 2m |
; |
у = 2000 + 2р1 – 10р2 + 3m, |
||
где x, p1 |
и |
y, |
p2 |
– спрос на товары А и В и их цены |
соответственно,
m – часть дохода потребителя, которую он расходует на приобретение названных товаров. Определить коэффициенты эластичности функций при p1 = 40, p2 = 50, m = 100.
Решение.
|
|
E xp |
|
|
|
p1 |
|
X p |
|
|
|
|
|
X p |
|
20. |
|
||||||||||||
|
|
|
|
|
X |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
E xp |
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
|
( |
20) |
1,8. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1000 |
20 |
|
40 |
|
|
50 |
200 |
|
|||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
E xp |
|
|
|
|
|
p2 |
X p |
|
|
|
|
50 |
1 |
|
0,11. |
|
|||||||||||
|
|
2 |
|
|
|
|
X |
2 |
|
|
450 |
|
|
||||||||||||||||
E yp |
|
p1 |
Yp |
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
2 |
0,043. |
|||||||
|
Y |
|
2000 |
|
|
80 |
500 |
|
300 |
||||||||||||||||||||
1 |
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||||
|
E yp |
|
|
|
p2 |
|
|
Yp |
|
|
|
50 |
|
( |
10) |
0,27. |
|||||||||||||
|
2 |
|
|
Y |
|
|
2 |
1880 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
E xm |
|
|
m |
|
X m |
|
|
100 |
|
|
2 |
|
0,44. |
|
|||||||||||||
|
|
|
|
|
X |
|
450 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
EYm |
|
|
m |
|
YM |
|
|
|
100 |
|
|
3 |
|
0,16. |
|
||||||||||||
|
|
|
|
Y |
|
|
1880 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Величины Ep1 (x)= -1,8 и Ep1(y)=0,043 показывают, что с ростом цены товара А на 1%, спрос на товар А снижается на 1,8%, а спрос на товар В повышается на 0,043%.
Аналогично величины Ер2(х) и Ер2(у) показывают, что с увеличением цены товара В на 1%, спрос на товар А повышается на 0,11%, а спрос на товар В снижается 0,27%.
4.6. Экстремум функции двух переменных
Пусть на множестве U задана функция Z=f(x,y).
Необходимое условие экстремума функции двух переменных -
равенство частных производных нулю. zx  fx (x, y) 0 zy
fx (x, y) 0 zy  fy (x, y) 0
fy (x, y) 0
Достаточное условие экстремума функции двух переменных.
Пусть (х0,у0) – критическая точка функции
Z=f(x,y) , т.е. fx (x0 , y0 ) 0 и |
fy (x0 y0 ) 0 , а значение вторых |
частных |
|
призводных функции z=f(x,y) |
есть fxx (x0 y0 ) A , fx, y (x0 y0 ) B , |
f yy (x0 y0 ) C |
|
Тогда
