
Сандракова Функтсии многикх переменныкх 2015
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ «МИФИ»
Е. В. Сандракова, Е.В. Сумин, М. М. Тищенко, В. П. Трифоненков
Функции многих переменных
Учебно-методическое пособие
Москва 2015
УДК 517.2(076.5) ББК 22.161.1я7 Ф94
Функции многих переменных. Учебно-методическое пособие /
Е.В. Сандракова, Е.В. Сумин, М.М. Тищенко, В.П. Трифоненков. – М.:
НИЯУ МИФИ, 2015. – 68 с.
Рассмотрены вопросы, связанные с дифференцируемой функцией многих переменных, дифференциалом функции в точке, неявными функциями, условным экстремумом, зависимостью и независимостью функций, дифференцируемыми отображениями и дифференциалом отображения.
Предназначено для студентов 1 курса 2 семестра всех факультетов НИЯУ МИФИ, а также может быть использовано преподавателями при проведении ими практических занятий по перечисленным разделам.
Рецензент д-р физ.-мат. наук, проф. НИЯУ МИФИ Д.Г. Орловский
ISBN 978-5-7262-2099-4 © Национальный исследовательский ядерный университет «МИФИ», 2015
Редактор М.В. Макарова
Подписано в печать 08.04.2015. Формат 60х84 1/16.
Уч.-изд. л. 4,25. Печ. л. 4,25. Тираж 100 экз.
Изд. № 007-1. Заказ № 51.
Национальный исследовательский ядерный университет «МИФИ». Типография НИЯУ МИФИ.
115409, Москва, Каширское ш., 31
Введение
В этой работе рассматриваются функции многих переменных и отображения евклидова n -мерного координатного пространства в евклидово пространство той же или иной размерности.
Представляют интерес вопросы дифференцируемости функции многих переменных, т.е. отображения
f : D → R1 ,
где D E n , D – открытая область евклидова пространства En ; отображения
f : En → En (n ≥ 2) ,
где Е п – два экземпляра п-мерного евклидова координатного пространства и отображения
f : En → Em (n ≥ 2, m ≥ 2) .
Несколько слов о структуре En , n ≥ 2 .
Рассмотрим совокупность всех упорядоченных наборов n действительных чисел {(x1,…, xn )} .
Любой упорядоченный набор п чисел можно трактовать:
1) как точку P(x1,…, xn ) п-мерного координатного пространства Rn в декартовой прямоугольной системе координат Ox1 …xn ;
2) как вектор с компонентами {x1,…, xn} , причем этот вектор можно рассматривать как радиус-вектор точки Р с координатами
(x1 ,…, xn ) :
r = OP ={x1,…, xn }.
Тогда с упорядоченными наборами п действительных чисел естественно производить операции сложения и умножения на числа из некоторого поля Λ. Будем в качестве Λ рассматривать поле вещественных чисел. Тогда
3
1)для x = (x1 ,…, xn ) и y = ( y1,…, yn ) определена операция сложения x + y = (x1 + y1 ,…, xn + yn ) ;
2)для x = (x1 ,…, xn ) и λ Λ = R1 определена операция умножения на число
λx = (λx1,…, λxn ) .
Эти две операции естественным образом удовлетворяют аксио-
мам линейного пространства над полем R1, причем θ = (0,…,0) (это
проверялось в курсе «Линейная алгебра»).
Введём теперь по аналогии с геометрическим пространством трёхмерных векторов скалярное произведение упорядоченной пары элементов x = (x1,…, xn ) и y = ( y1 ,…, yn ) как
n
(x, y) = ∑xk yk = x1 y1 +…+ xn yn .
k =1
При этом все аксиомы скалярного произведения выполняются.
Итак, линейное пространство Rn с введённым таким образом скалярным произведением элементов является евклидовым пространством, которое впредь будем обозначать En . В En вводим
норму 
 x
x
 En = (x, x) . Это дает возможность измерять углы между
En = (x, x) . Это дает возможность измерять углы между
векторами |
x = (x1,…, xn ) и y = ( y1 ,…, yn ) |
и длины векторов в En . |
||||||||||||
Если x ≠ θ, |
y ≠ θ , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
(x, y) |
|
∑xk yk |
||||||||||
|
cos(x, y) = |
= |
k =1 |
|
|
|
|
|
|
. |
||||
|
|
x |
|
y |
∑(xk )2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
∑( yk )2 |
||||||||
|
|
|
|
|
|
|
n |
|
n |
|||||
|
|
|
|
|
|
|
k =1 |
|
k =1 |
|||||
To, что для x En числовая функция |
|
x |
|
|
|
= (x, x) есть норма, |
||||||||
|
|
|
||||||||||||
проверяется непосредственно. Из свойств нормы следует, что есть возможность ввести в пространстве En ещё одну структуру –
структуру метрического пространства, положив для x, y En
4

n
ρ(x, y) = 
 x − y
x − y
 = ∑(xk − yk )2 , ρ(x,θ) =
= ∑(xk − yk )2 , ρ(x,θ) = 
 x
x
 .
.
k =1
Аксиомы метрики непосредственно проверяются.
В частности, если рассматривать упорядоченные наборы п действительных чисел как точки в En , то записывается неравенство треугольника для точек P(x1,…, xn ) , Q( y1,…, yn ) , R(z1 ,…, zn ) En
ρ(P, R) ≤ ρ(P,Q) + ρ(Q, R) .
Метрика ρ(P,Q) даёт возможность ввести сферическую или
прямоугольную окрестность точки в En . |
|
|
|||||
Определение. |
Сферической α-окрестностью точки P En |
на- |
|||||
|
|
|
|
|
|
0 |
|
зывается множество |
S |
α |
(P ) ={P En : ρ(P , P) < α, α > 0} . |
|
|||
|
|
|
0 |
0 |
|
|
|
В координатах |
P (x1 |
,…, xn ) , |
|
|
|
||
|
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
n |
|
|
Sα (P0 ) ={P(x1 ,…, xn ) En : ∑(xk − x0k )2 |
< α2 } . |
|
|||||
|
|
|
|
|
k=1 |
|
|
Определение. |
Прямоугольной |
β-окрестностью |
точки P En |
||||
0
называется множество
Tβ (P0 ) ={P(x1 ,…, xn ) En : xk − x0k <β, β > 0, k =1, 2,…, n} .
Справедлива теорема об эквивалентности систем прямоугольных и сферических окрестностей точки P0 En .
Введение окрестностей точки есть введение топологической
структуры в En , |
порождённой метрикой ρ |
E |
n |
. А это даёт возмож- |
|||||
|
|
|
|
|
|
|
|
|
|
ность ввести понятие |
предела точечной |
последовательности |
|||||||
{P } En , k =1, 2,… |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
Р0 в |
|
Определение. |
Говорят, что |
{P } |
сходится к |
En , если |
|||||
|
|
|
k |
|
|
|
|
|
|
ε > 0 K k > K Pk Sε (P0 ) . |
|
|
|
|
|
|
|||
Следовательно, это |
даёт |
возможность |
изучать |
функции |
|||||
f : D → R1 , где |
D En , |
а также |
отображения |
f : En → En и |
|||||
f : En → Em , исследуя их на непрерывность, дифференцируемость, вводя классы гладкости функций и отображений.
5

1. Дифференцируемая функция многих переменных. Дифференциал функции в точке.
Частные производные и дифференциалы высших порядков
Пусть D – открытая область в п-мерном пространстве En и точ-
ка P0 = P0 (x1 ,…, xk ,..., xn ) D .
Определение 1.1. Функция f (P) = f (x1 , x2 ,...xn ) : D → R1 назы-
вается дифференцируемой в точке P = P (x1 ,…, xk ,..., xn ) D , если |
||||||||||
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
ее приращение |
f (P0 ; P0 P) = f (P) − f (P0 ) |
в точке Р0, |
вызванное |
|||||||
вектором смещения P0 P , может быть представлено в виде |
||||||||||
|
f (P ; P P) = f (P) − f (P ) = A1 x1 |
+...An xn |
+ ω(P ; P P) , (1.1) |
|||||||
|
0 |
0 |
0 |
|
|
|
|
|
0 |
0 |
где Ai |
– действительные числа, k =1, 2,..., n , |
|
|
|
||||||
|
|
|
ω(P0 ; P0 P) = o(ρ) |
при ρ → 0 , |
|
|
||||
|
|
|
n |
|
|
|
|
|
|
|
где |
ρ =| P0 P |= |
∑( xk )2 , |
P0 (x01, x0 |
2 ,...x0n ), |
|
P(x1, x2 ,...xn ), |
||||
k=1
xk = xk − x0k , k =1, 2...n ; ρ – модуль вектора смещения или норма
P0 P En , ρ =|| P0 P ||E .
Определение 1.2. Главная линейная часть приращения
f (P0 , P0 P) |
|
функции f (P) в точке Р0, т.е. L(P0 P) = |
||
= A1 |
x1 +... + An |
xn называется дифференциалом функции f(P) в |
||
точке |
P = P (x1 |
,…, xn ) . |
||
|
0 |
0 |
0 |
0 |
Определение 1.3. Пусть f(P) – дифференцируемая функция в точке P0 D , приращение которой в точке Р0, вызванное вектором
смещения P0 P , представимо в виде (1.1). Тогда вектор с компонентами A1,..., An называется градиентом функции f(P) в точке Р0 и обозначается grad f |P0 ={A1,..., An }.
Итак, для дифференцируемой функции в точке Р0 приращение f (P0 ; P0 P) , вызванное вектором смещения P0 P , P0 P D пред-
ставимо в виде:
6
|
|
|
f (P0 ; P0 P) = (gradf |P , P0 P) + ω(P0 ; P0 P) , |
|||
|
|
|
|
|
0 |
|
где |
ω(P0 ; P0 P) = o(ρ) при |
ρ →0 , |
ρ =|| P0 P ||E =| P0 P | , и |
|||
L(P P) = (gradf | |
P |
, P P) R1 . |
|
|
||
0 |
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
Замечание 1.1. |
L(P P) = A1 |
x1 +... + An |
xn называется также |
|||
|
|
|
|
0 |
|
|
касательным отображением в точке P0 или производным отобра- |
||||||
жением в точке Р0 |
отображения |
f : D → R в точке P D Rn . |
||||
|
|
|
|
|
|
0 |
Рассмотрим теперь фиксированное направление в Еп, заданное
вектором |
l ≠ θ , и пусть e = l/ || l ||E = l/ | l | – единичный вектор за- |
данного направления. |
|
Будем смещаться из точки P0 D , не покидая области D, в на- |
|
правлении |
l , т.е. рассмотрим вектор смещения P P = te , t R1 , |
|
0 |
при этом P0 P D . Тогда смещение ρ =| P0 P |=| te |=| t | Определение 1.4. Производной функции f(P) в точке P0 D в
направлении l называется предел, если он существует,
|
|
|
lim |
|
f (P0 |
,te) |
= |
∂f |
|
, |
||
|
|
|
|
|
||||||||
|
|
|
|
t |
|
∂l |
|
|||||
где |
∂f |
|
t → 0 |
|
|
|
p0 |
|||||
|
|
|
||||||||||
|
– обозначение указанного предела. Обозначение произ- |
|||||||||||
|
||||||||||||
|
∂l |
|
p |
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
водной по направлению |
|
|
|
|
|
|
||||||
|
|
|
∂f |
|
|
= (grad f |P |
,e) . |
|||||
|
|
|
|
|||||||||
|
|
|
∂l |
|
p |
|
|
0 |
|
|
||
|
|
0 |
|
|
|
|
|
|
||||
Рассмотрим теперь специальные направления. Выберем в Еп
систему декартовых прямоугольных |
координат и, |
следовательно, |
||||
фиксированный базис в Еп: e ,...,e |
– ортонормированный базис |
|||||
|
|
|
1 |
n |
|
|
осей координат Ox1 ,…,Oxn . Сместимся из точки |
P0 (x01 ,..., x0n ) в |
|||||
точку P (x1 |
,..., xk −1 |
, xk , xk +1 ,..., xn ) |
в направлении базисного вектора |
|||
k 0 |
0 |
0 |
0 |
|
|
|
ek , k =1, 2,..., n : |
|
|
|
|
|
|
P P ={0, 0,..., xk |
− xk ,..0} = {0,0,..., xk ,..0} = |
xk e . |
||||
0 |
k |
|
0 |
|
|
k |
|
|
|
|
7 |
|
|
Получим производную функции f(P) в точке Р0 в направлении k-й координатной оси.
Определение 1.5. Частной производной функции f(P) =
= f (x1 ,..., xn ) |
|
в точке |
P (x1 |
,..., xn ) |
|
|
в направлении |
e |
называется |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
||
производная по направлению |
вектора ek в точке Р0, |
т.е. предел, |
|||||||||||||||||||||||||||||
если он существует |
f (P ; xk e ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
lim |
= lim |
|
f (P ) − f (P ) |
= |
|
|
|
||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
k |
|
|
|
|
|
0 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
xk |
|
|
|
|
|
xk |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
xk →0 |
|
|
|
|
|
|
|
|
|
xk →0 |
|
|
|
|
|
|
|
|
|
|
||||||||
= |
lim |
f (x1 ,.., xk −1 , xk , xk +1 |
,.., xn |
) − f (x1 ,..., xn ) |
= |
|
|||||||||||||||||||||||||
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
0 |
|
0 |
|
|
|
|
0 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xk |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
xk →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= lim |
|
f (x1 |
,.., xk −1 , xk |
+ |
|
xk , xk +1 ,.., xn ) − f (x1 |
,..., xn ) |
. |
|||||||||||||||||||||||
|
|
0 |
|
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk |
|
|
|
|
|
|
|
|
|
|
||||||
xk →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Обозначается частная производная функции f (P) = f (x1 ,..., xn ) |
|||||||||||||||||||||||||||||||
в точке Р0 по переменной хk через |
f (P ; |
xk e ) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
∂f |
|
= lim |
|
. |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
k |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
∂xk |
|
|
|
|
|
|
|
xk |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
P |
|
|
xk →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя обозначения частных производных |
|
|
∂f |
|
= f ′k , полу- |
||||||||||||||||||||||||||
|
|
∂xk |
|||||||||||||||||||||||||||||
чаем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
grad f |
|
|
|
∂f |
|
|
∂f |
|
|
{fx′1 ,.., fx′n } |
|
|
|
|
||||||||||||||
|
|
|
|P0 |
= |
|
|
|
,... |
|
|
|
|
= |
|
|
|
|
||||||||||||||
|
|
|
|
1 |
∂x |
n |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
в точке P0 и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂f |
|P = (grad |
f |
|P ,e) = |
∂f |
|
|P |
|
α1 |
+... + |
|
∂f |
|
|
|P αn |
, |
|
|||||||||||||||
∂l |
∂x |
|
|
|
∂x |
n |
|
||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|||
где αi = cosϕi , |
e |
={α1 ,...,αn} ={cos ϕ1 ,...,cos ϕn } |
(ϕi – угол между |
||||||||||||||||||||||||||||
вектором e и положительным направлением оси Oxi ).
Далее, сформулируем определение дифференцируемости функции в точке и рассмотрим связанные с ним понятия для случая функции двух переменных (для переменных в формулировках будут использованы такие обозначения, которые приняты в рассматриваемых ниже примерах).
Пусть п = 2, D R2 . В R2 выбрана декартова прямоугольная система координат Оху, D – открытая область в R2, P0 (x0 , y0 ) D
8
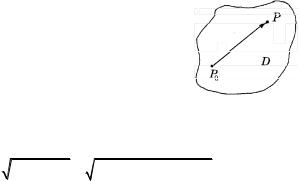
(Р0 – внутренняя точка, P(x, y) – произвольная
точка из D) (рис.1.1).
Пусть на D определена функция двух переменных u = f (x, y) . Рассмотрим произвольный
вектор смещения
P0 P ={x − x0 , y − y0 } ={ x, y}; |
|
Рис. 1.1 |
|
x = x − x0 x = x0 + x ; |
|
||
|
|
||
y = y − y0 y = y0 + y ; |
|
||
ρ =| P P |= x2 + y2 |
= (x − x )2 |
+( y − y |
)2 . |
0 |
0 |
0 |
|
И пусть P0 P – геометрический отрезок, целиком лежащий в D , т.е. смещаясь из точки Р0 в Р мы не покидаем области D. Тогда вектор смещения P0 P вызовет приращение функции
f (P0 ; P0 P) = f (P) − f (P0 ) = f (x, y) − f (x0 , y0 ) =
= f (x0 + x, y0 + y) − f (x0 , y0 ) .
Определение 1.6. Функция двух переменных f(х, у) называется дифференцируемой в точке Р0(х0, у0), если ее приращение
f (P0 ; P0 P) в точке Р0, вызванное вектором смещения P0 P , можно представить в виде:
f (P ; P P) = A1 |
x + A2 |
y +ω(P ; P P) , |
(1.2) |
||
0 |
0 |
|
0 |
0 |
|
где А1, А2 – числа, не зависящие от P0 P , но меняющиеся, если ме-
нять точку Р0, а ω(P0 ; P0 P) = ο(ρ) – бесконечно малая величина бо-
лее высокого порядка относительно смещения ρ при ρ → 0. Определение 1.7. Пусть функция f(P) такова, что имеет место
(1.2). Главная линейная часть |
A1 x + A2 y |
приращения функции, |
||
т.е. линейная функция |
L(P0 P) = L( |
x, y) , |
называется дифферен- |
|
циалом функции f (x, y) |
в |
точке |
Р0 и обозначается |
|
df |p = A1 x + A2 y . |
|
|
|
|
0 |
|
|
|
|
Замечание 1.2. Если |
f : D → R1 , |
D E2 , то L(P P) – линейное |
||
|
|
|
|
0 |
приближение ( P P E2 |
в точке Р0) отображения f(P) в точке Р0: |
|||
0 |
|
|
|
|
9
L : E2 → R1 ,
Здесь можно считать, что оно берется в точке Р0. Его называют касательным пространством в точке Р0 к пространству Е2, в области
D которого задан вектор смещения P0 P.
Теорема 1.1 (необходимые условия дифферецируемости).
Пусть функция f(P) определена на открытой области D En и дифференцируема в точке P0 D . Тогда в этой точке Р0 функция f(P) непрерывна, имеет производную по любому направлению l,
при этом |
∂f |
|
= (grad f |P ,e) , где e – единичный вектор направ- |
|
|||
|
∂l |
|
p |
|
|
|
0 |
|
|
|
0 |
|
|
|
ления l, в частности, f(P) имеет частную производную по каждой
своей переменной x1 ,..., xn и |
|
∂f |
|
= = (grad f | |
|
,e ) , где |
e |
– |
|||
|
|
|
|||||||||
|
|
|
|||||||||
|
|
|
|
∂xk |
|
p |
|
P0 |
k |
k |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
единичный вектор оси Oxk |
декартовой прямоугольной системы |
||||||||||
координат |
Ox1...xn , отвечающей |
|
ортонормированному базису |
||||||||
e ....,e |
в евклидовом пространстве En . |
|
|
|
|
|
|||||
1 |
n |
|
|
|
|
|
|
|
|
|
|
Функция |
может иметь |
все |
|
частные |
производные |
∂f |
, |
||||
|
∂xk |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k =1, 2,..., n , и даже производную по любому направлению l в некоторой точке, но не быть в этой точке дифференцируемой.
Пример 1.1. Показать, что у функции
f (x1 , x2 ) = 0, x1 x2 = 0,1, x1 x2 ≠ 0
существуют обе частные производные в точке О (0,0), но она не является дифференцируемой в этой точке.
Решение. Эта функция имеет частные производные в точке
О(0,0).
Выбрав |
P P = OP ={ |
x1 |
, 0}, x1 = x1 −0 = x1 , x1 ≠ 0, получаем |
||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
∂f |
|
= lim |
|
f (x1 |
, x2 ) − f (0, 0) |
|
= lim |
|
f (x1 ,0) − f (0, 0) |
= |
||
|
|
|
|||||||||||
|
∂x1 |
|
|
x1 |
|
|
x1 |
||||||
|
|
O(0, 0) x1 →0 |
|
x1 →0 |
|
|
|||||||
|
|
|
|
|
|
||||||||
|
|
|
= lim |
f ( |
x1 , 0) − f (0, 0) |
= lim |
0 −0 |
= 0 . |
|
||||
|
|
|
|
|
x1 |
|
|
||||||
|
|
|
x1 →0 |
|
x1 →0 |
x1 |
|
||||||
10
