Сандракова Функтсии многикх переменныкх 2015

Найдем дифференциал от обеих частей полученных тождеств:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

∂∂Fx1n dx1 +…+ ∂∂xFmn dxm + ∂∂Fyn1 dy1 +…+ ∂∂Fynn dyn ≡ 0 .

Рассмотрим полученные равенства как систему уравнений относительно дифференциалов dy1 ,…, dyn . Заметим, что определителем этой системы является якобиан системы функций

Fi (x1 ,…, xm , y1 ,…, yn ) (i =1,2,…, n) по переменным y1 ,…, yn , который в силу выполнения условий теоремы отличен от 0. Поэтому, в силу теоремы Крамера, эта система однозначно разрешима.

. . . . . . . . . . . . . . . . . . . . . . .

k=1,…,n) (это коэффициенты при dxi в выражении для dyk). Будем считать, что на 1-м шаге мы получили систему равенств:

31

На следующем шаге необходимо найти 1-й дифференциал от обеих частей равенств в (2.20).

Запишем для примера, как будет выглядеть 1-я строка:

чим выражения для d2yk (k = 1, ..., n). Сравнив полученные выражения с

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Для нахождения последующих производных процесс повторяет-

ся.

Пример 2.8. Найти dxdz и dydz , если

Решение. Для нахождения требуемых производных будем считать, что система (2.21) определяет переменные х и у как функции переменной z. Запишем матрицу Якоби

32

Рассматривается окрестность точки P0 (x0 , y0 , z0 ) , где x0 ≠ y0 , в

Решение. Для нахождения указанных производных будем считать, что система (2.22) определяет и = и(х, у), v = v(x, y), z = z(x, y). Далее имеем

33

3. Условный экстремум

Пусть G En , G – открытое множество. На G заданы функции f(x) и ϕi (x) , i =1, 2,…, m ; x = (x1 ,…, xn ) G . Обозначим через

точкой условного экстремума функции f(x) относительно (или при выполнении) уравнений связи (3.2), если она является точкой обычного экстремума этой функции, рассматриваемой только на множестве E. (Точка x0 E называется точкой строгого условного

максимума (минимума) функции f(x) относительно уравнений свя-

Пример 3.1. Пользуясь методом исключения, найти условные экстремумы функции

f (x, y) = x2 + y2

34

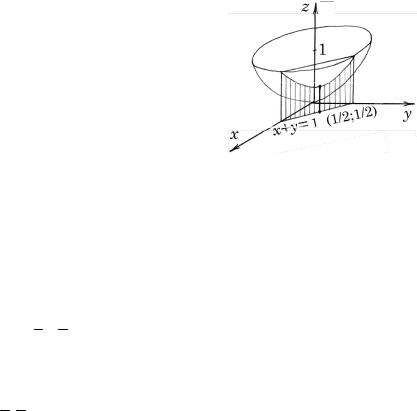
относительно уравнения связи x + y – 1 = 0.

Решение. Функция f(x, у) является функцией двух переменных. Одно уравнение связи позволяет выразить одну переменную через оставшиеся, т.е. в данном случае через одну независимую перемен-

ную у = 1 – х.

При выполнении уравнения свя-

зи функция f(x, у) становится функцией одной переменной f (x) = f (x, 1 − x) = x2 +(1− x)2 = 2x2 −2x +1 .

Для функции одного переменного экстремум определяется по

y =1 − 12 = 12 является точкой условного экстремума функции f(x, у)

при наличии уравнения связи х + у – 1 = 0. Геометрически это означает, что точка параболоида z = x2 + y2 , находящаяся над точкой

12 ; 12 , является самой низкой из всех точек, лежащих над прямой

х + у = 1 (рис. 3.1).

Отметим, что (0; 0) – это точка обычного экстремума функции f (x, y) = x2 + y2 , т.е. в данном случае обычный и условный экстре-

мумы достигаются в разных точках.

Рассмотрим способ решения задачи об условном экстремуме, приведенный в примере 3.1, в общем случае.

Предположим, что:

1) функции f(x) и ϕi (x) , i =1, 2,…, m имеют непрерывные частные производные первого порядка на G;

35

Это означает, что функции системы (3.2) независимы, и в силу

Подставляя в функцию y = f(x) выражения (3.4), получим функцию

от переменных x1 ,…, xn−m , определённую и непрерывно дифференцируемую в окрестности точки x0 = (x10 , x02 ,…, x0n−m ) .

Точка x0 является точкой (строгого) условного экстремума для функции f(x) относительно уравнений связи (3.2) тогда и только тогда, когда точка x0 является точкой обычного (строгого) экстре-

мума функции f (x1 , x2 ,…, xn−m ) .

Метод сведения задачи об условном экстремуме к задаче об обычном экстремуме удобен в случае, когда система (3.2) легко разрешима. Однако на практике часто решение (3.2) в явном виде бывает либо невозможно, либо весьма затруднительно. В этих случаях для решения задачи об условном экстремуме может быть использован метод множителей Лагранжа.

36

где λ1 ,…, λm – произвольные числа.

При произвольных λ1 ,…, λm точка условного экстремума для f(x) является точкой условного экстремума и для Φ(x;λ1 ,…,λm ) (и наоборот), поскольку на множестве E допустимых точек ϕi ≡ 0 и

f(x) совпадает с Φ(x;λ1 ,…,λm ) .

Теорема 3.1 (необходимые условия). Пусть точка x0 является точкой условного экстремума функции f(x) при выполнении уравнений связи (3.2). Тогда существуют такие числа λ1 ,…, λm , что в точке

Следствие. Уравнения (3.7) можно рассматривать как запись

Φ(x;λ1 ,…,λm ) , определённой в (3.6). Тогда теорему можно пере-

формулировать следующим образом. Если точка x0 является точкой условного экстремума для f(x), то существуют такие числа λ1 ,…, λm , что в точке x0

∂∂Φxi = 0 , i =1, 2,…,n ,

т.е. x0 – стационарная точка для Φ(x;λ1 ,…,λm ) .

Доказательство. Пусть x0 = (x10 ,…, x0n ) – точка условного экстремума для f(x), и пусть в этой точке, для определённости, выполняется условие (3.3). Тогда точка x0 = (x10 ,…, x0n−m ) является точкой

обычного экстремума для функции f , и поэтому в точке ~x0 df (x1 ,…, xn−m ) = 0 .

Пользуясь инвариантностью формы первого дифференциала для f, имеем

df (x1 ,…, xn−m , ψ1 ,…,ψm ) = 0

или

37

dxn−m+1 , …,dxn – дифференциалы функций ψ1 ,ψ2 ,…,ψm в точке x0.

Умножим равенства (3.9) для ϕi на произвольные константы λi, i =1, 2,…, m , и, сложив их между собой и с равенством (3.8), полу-

чим

Отметим, что первые n – m дифференциалов dxj являются независимыми, а dxn−m+1 ,…, dxn выражаются через dx1 ,…, dxn−m .

Выберем λ1 ,…,λm так, чтобы в точке x0 сомножители при зави-

симых дифференциалах обратились в нуль, т.е. выполнялись равенства

Это всегда возможно, так как система (3.11) является системой m линейных относительно λ1 ,…,λm уравнений с определителем

(см. условие (3.3)).

Таким образом, уравнение (3.10) приводится к виду

где dx1 ,…, dxn−m – дифференциалы независимых переменных, откуда и следует, что

38

Следовательно, доказано существование таких λ1 ,…,λm , что

выполнены условия (3.11) и (3.12), т.е. условия (3.7) теоремы.

Для решения задачи об условном экстремуме с использованием метода множителей Лагранжа составим функцию Ф(х) (см. (3.6)). Далее, получим систему, которая состоит из п уравнений (3.7), определяющих равенство нулю частных производных Φ(x;λ1 ,…,λm ) ,

и т уравнений связи (3.2):

Эта система определяет координаты точки x0 и коэффициенты λ1 ,…,λm , т.е. п + т неизвестных. Решая систему (3.13), лучше сна-

чала выразить λi. Сформулируем также достаточные условия экстремума.

Теорема 3.2 (достаточные условия). Если точка x0 = (x10 ,…, x0n )

удовлетворяет уравнениям связи (3.2) и является стационарной для функции Лагранжа (3.6), и если второй дифференциал функции Лагранжа в этой точке является положительно (отрицательно) оп-

ределённой квадратичной формой переменных dx1 ,…,dxn при условии, что они удовлетворяют системе уравнений (3.9), то точка х0 является точкой условного строгого минимума (максимума) для функции f ( x) относительно уравнений связи (3.2).

Значит, например, если:

х0, то х0 – точка условного строгого минимума (максимума).

39

Пример 3.2. Пользуясь методом Лагранжа, найти точки экстремума функции f (x, y) = xy , когда точка (х, у) лежит на прямой

х – у = 0.

Решение. Функция Лагранжа

Φ(x, y;λ) = f (x, y) +λϕ(x, y) = xy +λ(x − y) .

Запишем систему для определения коэффициента λ и координат

Точка (0;0) удовлетворяет необходимому условию экстремума. Второй дифференциал и уравнение связи в дифференциальной форме

d 2Φ = 2dxdy; d 2Φ = 2(dx)2 .dx −dy = 0

Заметим, что второй дифференциал d 2Φ = 2dxdy , являющийся

знакопеременной квадратичной формой в случае независимых переменных dx и dy, при выполнении уравнений связи (т.е. условия dx = dy) становится положительно определённой квадратичной формой переменной dx. Значит, в точке (0; 0) достигается строгий условный минимум функции f(x, y).

Предположим, что материальная точка находится под действием силы, которой соответствует потенциальная энергия, заданная функцией f (x, y, z) . Если эта точка может двигаться лишь по по-

верхности, определяемой уравнением ϕ(x, y,z) =0 (или по линии, которая задается системой двух уравнений

ϕ1 (x, y, z) = 0;ϕ2 (x, y, z) = 0,

соответственно, как линия пересечения двух поверхностей), то положение её равновесия будет определяться как условный экстре-

40