
1.3 Прямая на плоскости
Справедливо
следующее утверждение: если на плоскости
![]() фиксирована произвольная декартова
прямоугольная система координат
фиксирована произвольная декартова
прямоугольная система координат
![]() ,
то всякое уравнение первой степени с
двумя переменными
,
то всякое уравнение первой степени с
двумя переменными
![]() и
и
![]() (линейное уравнение) определяет
относительно этой системы координат
прямую линию.
(линейное уравнение) определяет
относительно этой системы координат
прямую линию.
Уравнение
![]() (10)
(10)
с произвольными
коэффициентами
![]() и
и
![]() таким, что
таким, что
![]() и
и
![]() не равны нулю одновременно, называется
общим
уравнением прямой.
не равны нулю одновременно, называется
общим
уравнением прямой.
В курсе аналитической
геометрии доказывается, что прямая,
определяемая общим уравнением (10),
перпендикулярна вектору
![]() .
Этот вектор называется нормальным
вектором прямой (10).
.
Этот вектор называется нормальным
вектором прямой (10).
Каноническим уравнением прямой называется уравнение вида
![]() ,
(11)
,
(11)
или
![]() ,
(12)
,
(12)
Уравнение (11) –
уравнение прямой, проходящей через
заданную точку
![]() ,
параллельно некоторому вектору
,
параллельно некоторому вектору
![]() ,
который называется направляющим
вектором
прямой.
,
который называется направляющим
вектором
прямой.
Уравнение (12) –
уравнение прямой, проходящей через две
данные точки
![]() и
и
![]() .
.
Уравнением прямой с угловым коэффициентом называется уравнение
![]() ,
(13)
,
(13)
где
![]() угловой
коэффициент, равный тангенсу угла
наклона прямой к положительному
направлению оси
угловой
коэффициент, равный тангенсу угла
наклона прямой к положительному
направлению оси
![]() ордината
точки
ордината
точки
![]() ,
в которой прямая, не параллельная оси
,
в которой прямая, не параллельная оси
![]() ,
пересекает эту ось.
,
пересекает эту ось.
Уравнение прямой,
не проходящей через начало координат
и пересекающей оси координат в точках
![]() и
и
![]() ,
может быть записано в виде (уравнение
в отрезках на осях):
,
может быть записано в виде (уравнение
в отрезках на осях):
![]() .
(14)
.
(14)
Если заданы
произвольная точка
![]() и произвольный вектор
и произвольный вектор
![]() ,
то параметрические уравнения прямой,
проходящей через данную точку, параллельно
данному вектору, имеют вид:
,
то параметрические уравнения прямой,
проходящей через данную точку, параллельно
данному вектору, имеют вид:
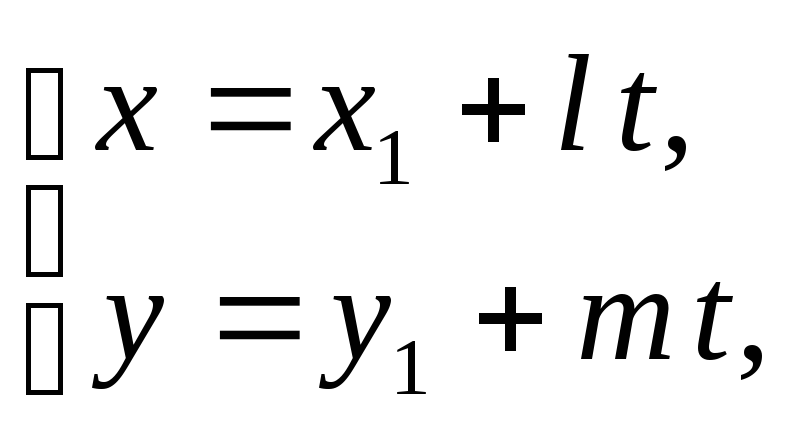 (15)
(15)
где
![]() .
.
Уравнение прямой,
проходящей через заданную точку
![]() ,
перпендикулярно вектору
,
перпендикулярно вектору
![]() ,
имеет вид:
,
имеет вид:
![]() .
(16)
.
(16)
Пусть
![]() угол
от положительного направления оси
угол
от положительного направления оси
![]() до луча
до луча
![]() ,
проходящего через начало координат,
перпендикулярного к прямой и пересекающего
эту прямую, а
,
проходящего через начало координат,
перпендикулярного к прямой и пересекающего
эту прямую, а
![]() расстояние
от начала координат до прямой. Тогда
уравнение прямой может быть записано
в виде:
расстояние
от начала координат до прямой. Тогда
уравнение прямой может быть записано
в виде:
![]() .
(17)
.
(17)
Уравнение (17) называется нормальным уравнением прямой.
Общее уравнение прямой (10) приводится к виду (17) путём умножения на нормирующий множитель
![]() .
.
В результате получается
![]() .
.
Знак нормирующего
множителя противоположен знаку
![]() в уравнении (10). Если в общем уравнении
в уравнении (10). Если в общем уравнении
![]() ,
то знак
,
то знак
![]() выбирается произвольным образом.
выбирается произвольным образом.
Расстояние
![]() от точки
от точки
![]() до прямой, заданной общим уравнением
(10) определяется по формуле:
до прямой, заданной общим уравнением
(10) определяется по формуле:
![]() .
(18)
.
(18)
Если две прямые
![]() и
и
![]() заданы уравнениями:
заданы уравнениями:
![]()
то косинус угла
![]() между ними определяется по формуле:
между ними определяется по формуле:
![]() .
(19)
.
(19)
Условие параллельности
прямых
![]() и
и
![]() ,
если известны координаты нормальных
векторов
,
если известны координаты нормальных
векторов
![]() и
и
![]() ,
эквивалентно условию коллинеарности
векторов
,
эквивалентно условию коллинеарности
векторов
![]() и
и
![]() ,
заключается в пропорциональности
координат этих векторов, то есть имеет
вид:
,
заключается в пропорциональности
координат этих векторов, то есть имеет
вид:
![]() .
(20)
.
(20)
Условие
перпендикулярности прямых
![]() и
и
![]() выражается равенством нулю скалярного
произведения
выражается равенством нулю скалярного
произведения
![]() .
Оно имеет вид:
.
Оно имеет вид:
![]() .
(21)
.
(21)
Если известны
координаты направляющих векторов
![]() и
и
![]() ,
то условия параллельности и
перпендикулярности прямых записываются
аналогично условиям (20) и (21) соответственно.
,
то условия параллельности и
перпендикулярности прямых записываются
аналогично условиям (20) и (21) соответственно.
Если прямые
![]() и
и
![]() заданы уравнениями с угловым коэффициентом
вида (13), то угол между этими прямыми
можно определить по формуле:
заданы уравнениями с угловым коэффициентом
вида (13), то угол между этими прямыми
можно определить по формуле:
![]() .
(22)
.
(22)
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Записать
уравнение прямой, проходящей через
точку
![]() ,
параллельно вектору
,
параллельно вектору
![]() .
.
Решение. Воспользуемся уравнением (11), тогда уравнение прямой будет иметь вид:
![]() .
.
Задача 2. Составить
уравнение прямой, проходящей через две
точки
![]() и
и
![]() .
.
Решение. Воспользуемся каноническим уравнением прямой (12):
![]() .
.
Подставляя вместо
![]() и
и
![]() координаты точек
координаты точек
![]() и
и
![]() соответственно, получим:
соответственно, получим:
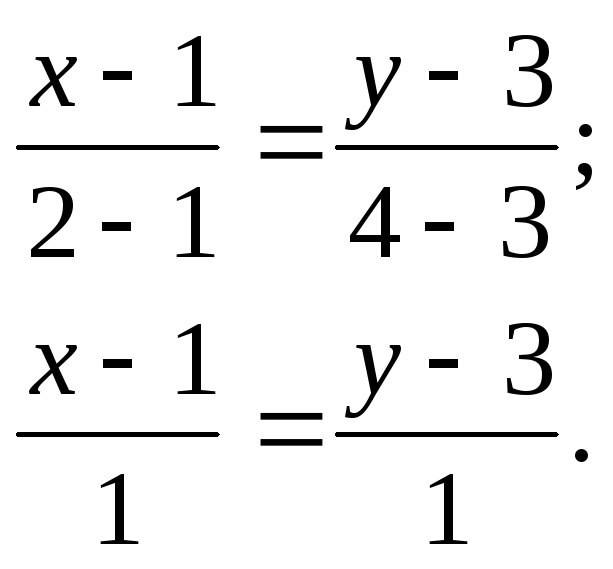
Уравнение прямой можно записать в общем виде:
![]() .
.
Задача 3. Составить
уравнение прямой, проходящей через
начало координат и наклонённой к оси
![]() под углом 300.
под углом 300.
Решение.
Так как прямая проходит через начало
координат, то в уравнении
![]() (13),
(13),
![]() .
Уравнение прямой будет иметь вид
.
Уравнение прямой будет иметь вид
![]() .
Так как
.
Так как
![]() ,
то окончательно получаем:
,
то окончательно получаем:
![]() .
.
Задача 4. Написать
уравнение прямой, проходящей через
точку
![]() перпендикулярно вектору
перпендикулярно вектору
![]() .
.
Решение. Уравнение прямой запишем в виде (16):
![]() .
.
По условию задачи
![]() .
.
![]() .
.
Раскрыв скобки, получим общее уравнение прямой:
![]() .
.
Задача 5. Написать
параметрические уравнения прямой,
проходящей через точку
![]() параллельно вектору
параллельно вектору
![]() .
.
Решение. Воспользуемся формулами (15):
![]() ,
,
![]() .
.
Задача 6. Составить уравнение прямой, отсекающей на осях координат отрезки 3 и 5.
Решение. Воспользуемся формулой (14). Уравнение прямой в отрезках на осях:
![]() .
.
Задача 7. Записать
уравнение прямой
![]() в отрезках на осях.
в отрезках на осях.
Решение. Разделим обе части уравнения на (-5):
![]() ,
,
![]() .
.
Здесь
![]() .
.
Задача 8. Определить
площадь треугольника, заключённого
между осями координат и прямой
![]() .
.
Решение.
Данный треугольник – прямоугольный,
катеты которого представляют собой
отрезки, отсекаемые прямой на координатных
осях. Запишем уравнение
![]() в отрезках на осях:
в отрезках на осях:
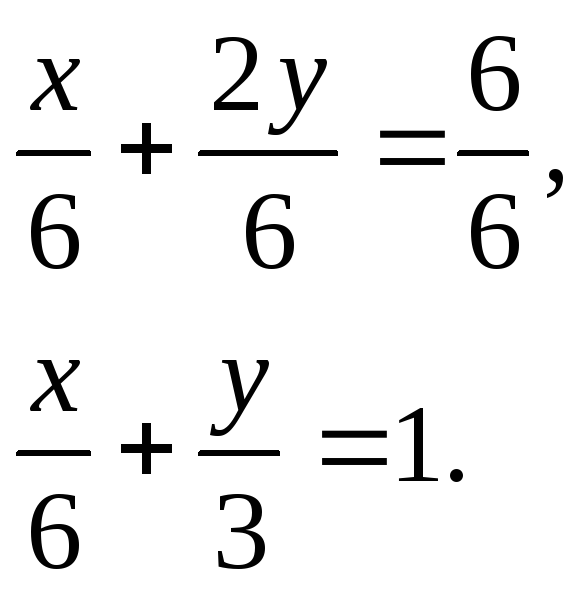
Здесь
![]() .
.
Задача 9. Заданы
прямая
![]() :
:
![]() и точка
и точка
![]() .
Требуется:
.
Требуется:
вычислить расстояние
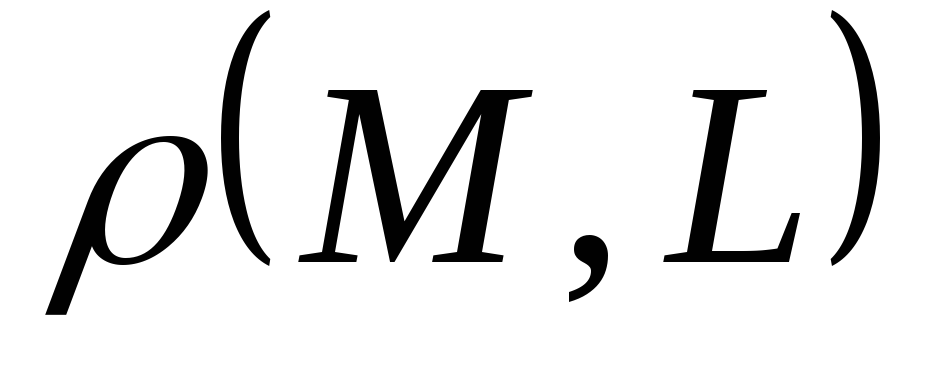 от точки
от точки
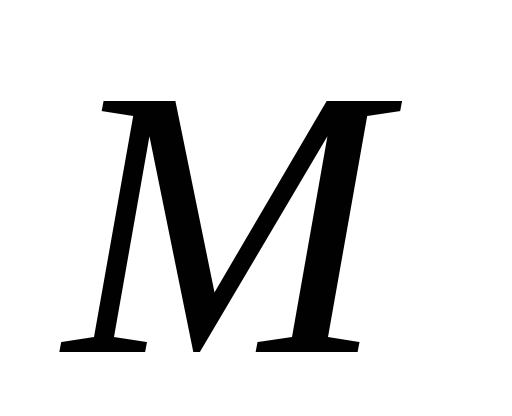 до прямой
до прямой
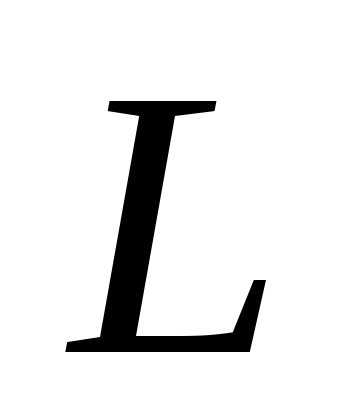 ;
;написать уравнение прямой
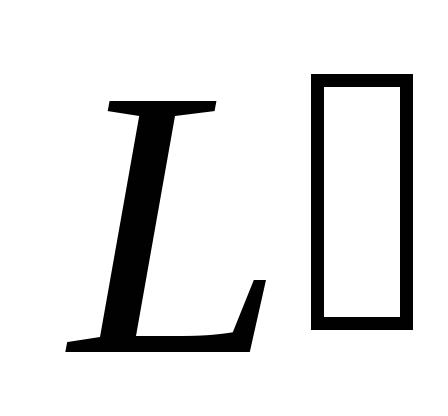 ,
проходящей через точку
,
проходящей через точку
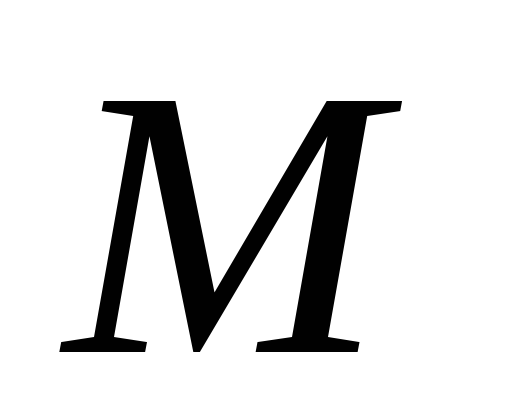 перпендикулярно заданной прямой
перпендикулярно заданной прямой
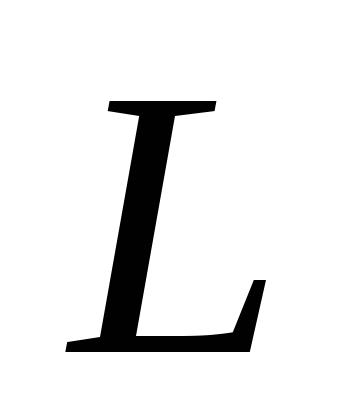 ;
;написать уравнение прямой
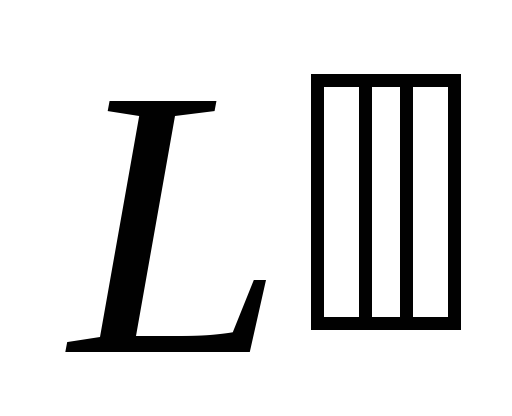 ,
проходящей через точку
,
проходящей через точку
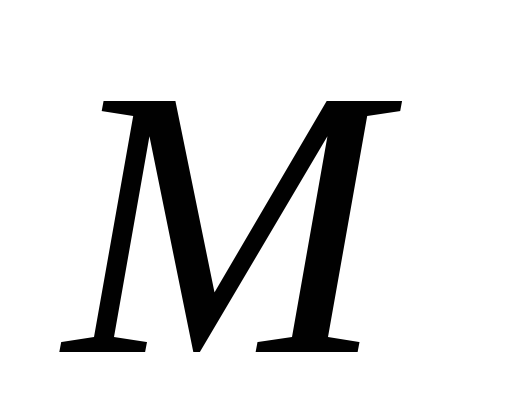 параллельно заданной прямой
параллельно заданной прямой
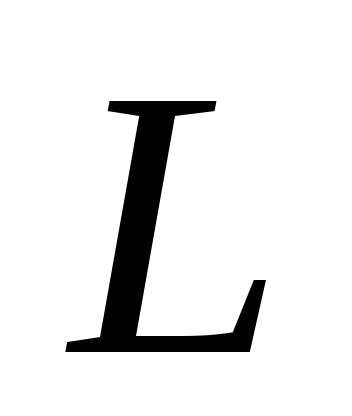 .
.
Решение.
1) Расстояние от
точки
![]() до прямой
до прямой
![]() можно вычислить по формуле (18). По условию
задачи имеем, что
можно вычислить по формуле (18). По условию
задачи имеем, что
![]() .
Подставляя эти значения в данную формулу,
получим:
.
Подставляя эти значения в данную формулу,
получим:
![]() .
.
2) Нормальный вектор
заданной прямой
![]() :
:
![]() .
Так как прямая
.
Так как прямая
![]() проходит через точку
проходит через точку
![]() перпендикулярно заданной прямой
перпендикулярно заданной прямой
![]() ,
то направляющий вектор
,
то направляющий вектор
![]() прямой
прямой
![]() равен нормальному вектору
равен нормальному вектору
![]() прямой
прямой
![]() ,
т.е.
,
т.е.
![]() .
.
Подставляя
координаты точки
![]() и вектора
и вектора
![]() в уравнение (11), получаем
в уравнение (11), получаем
![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
3) По условию задачи
прямая
![]() проходит через точку
проходит через точку
![]() параллельно заданной прямой
параллельно заданной прямой
![]() ,
следовательно, прямые
,
следовательно, прямые
![]() и
и
![]() имеют один и тот же вектор нормали, т.е.
имеют один и тот же вектор нормали, т.е.
![]() .
.
Подставляя
координаты точки
![]() и вектора
и вектора
![]() в уравнение 916), получим
в уравнение 916), получим
![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Ответ. 1)
![]() ;
2)
;
2)
![]() :
:
![]() ;
3)
;
3)
![]() :
:
![]() .
.
Задача 10. Установить
взаимное расположение прямых
![]() и
и
![]() .
Если прямые пересекаются, найти их точку
пересечения.
.
Если прямые пересекаются, найти их точку
пересечения.
Решение. Условия параллельности и перпендикулярности прямых не выполняются.
Вектор нормали
первой прямой имеет координаты
![]() ,
второй прямой –
,
второй прямой –
![]() .
.
![]() и
и
![]() .
.
Следовательно, прямые пересекаются. Точка пересечения принадлежит и первой и второй прямой. Её координаты найдём из системы уравнений:
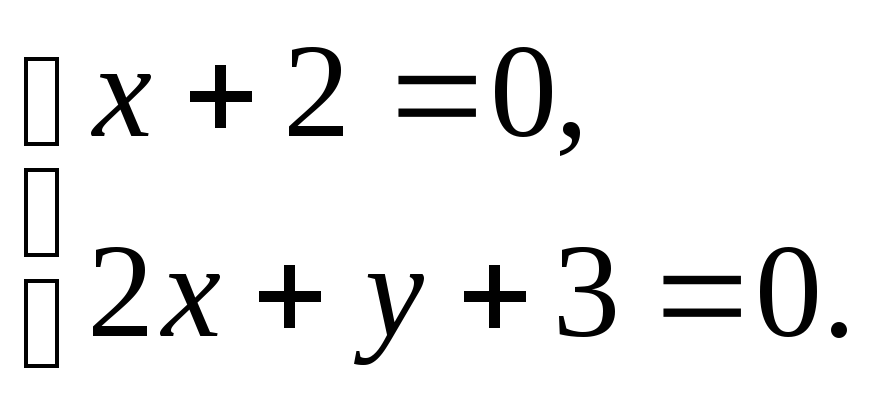
Отсюда получаем
![]() ,
,
![]() .
Точка пересечения имеет координаты
.
Точка пересечения имеет координаты
![]() .
.
Задача 11. Треугольник
![]() задан координатами своих вершин:
задан координатами своих вершин:
![]() ,
,
![]() и
и
![]() .
Требуется:
.
Требуется:
1) Написать уравнение
стороны
![]() ;
;
2) Написать уравнение
высоты
![]() ,
опущенной из вершины
,
опущенной из вершины
![]() на сторону
на сторону
![]() и вычислить её длину
и вычислить её длину
![]() ;
;
3) Найти угол
![]() между высотой
между высотой
![]() и медианой
и медианой
![]() .
.
Решение.
1) Воспользуемся уравнением прямой, проходящей через две заданные точки (12):
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
2) Уравнение высоты
![]() есть уравнение прямой, проходящей через
точку
есть уравнение прямой, проходящей через
точку
![]() перпендикулярно
перпендикулярно
![]() .
.
Нормальный вектор
прямой
![]() ,
имеющий координаты
,
имеющий координаты
![]() можно взять в качестве направляющего
вектора искомой прямой, так как он будет
ей перпендикулярен. Подставляя координаты
вектора
можно взять в качестве направляющего
вектора искомой прямой, так как он будет
ей перпендикулярен. Подставляя координаты
вектора
![]() и точки
и точки
![]() в уравнение (11), получаем:
в уравнение (11), получаем:
![]() :
:
![]() ;
;
![]() .
.
Раскрыв скобки,
получим уравнение высоты
![]() в общем виде:
в общем виде:
![]() .
.
Длина
![]() это
расстояние от точки
это
расстояние от точки
![]() до прямой
до прямой
![]() .
Вычислим его по формуле (18).
.
Вычислим его по формуле (18).
![]() .
.
3) По определению
медианы точка
![]() середина
отрезка
середина
отрезка
![]() .
Её координаты находятся по следующим
формулам:
.
Её координаты находятся по следующим
формулам:
![]() .
Подставляя координаты точек
.
Подставляя координаты точек
![]() и
и
![]() ,
получаем:
,
получаем:
![]() .
.
Таким образом,
![]() .
.
Составим уравнение
медианы
![]() как уравнение прямой, проходящей через
две заданные точки (12).
как уравнение прямой, проходящей через
две заданные точки (12).
![]() :
:
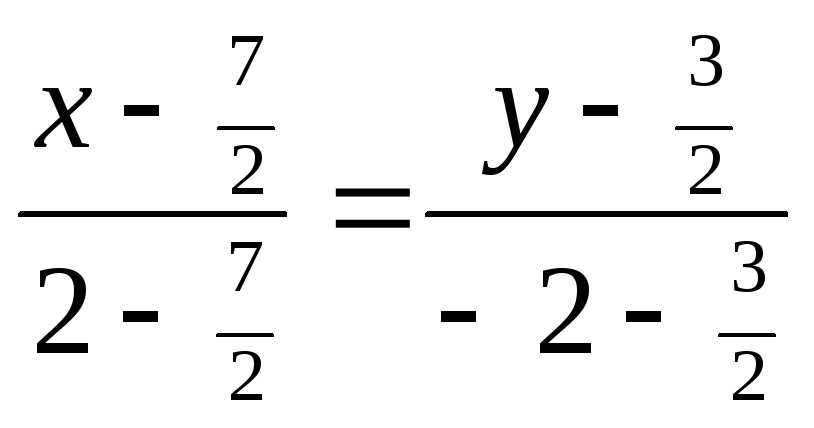 ;
;
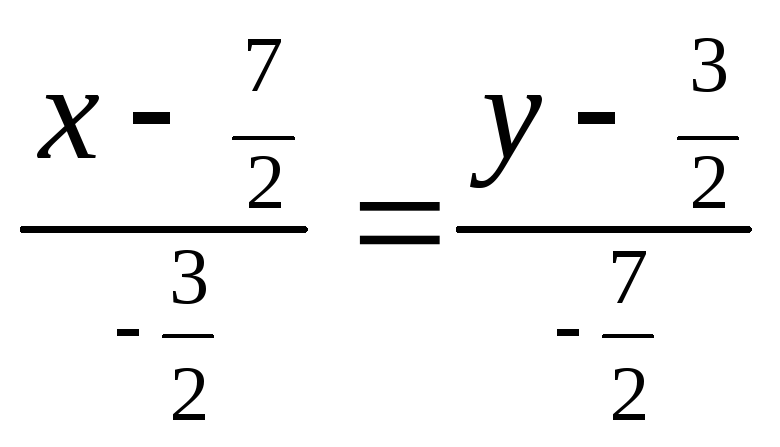 ;
;
![]() ;
;
![]() ;
;
![]() .
.
Чтобы найти угол
между высотой
![]() и медианой
и медианой
![]() ,
достаточно найти угол между нормальными
векторами этих прямых.
,
достаточно найти угол между нормальными
векторами этих прямых.
![]() .
.
Подставим координаты данных векторов в уравнение (7):
![]() .
.
![]() .
.
Ответ. 1)
![]() :
:
![]() ;
2)
;
2)
![]() :
:
![]() ,
,
![]() ;
;
3)
![]() .
.
Задача 12. Определить
положение точки
![]() относительно прямой
относительно прямой
![]() .
.
Решение.
Подставим координаты точки
![]() в уравнение прямой :
в уравнение прямой :
![]() .
Следовательно, пара чисел не является
решением уравнения
.
Следовательно, пара чисел не является
решением уравнения
![]() и точка
и точка
![]() не принадлежит прямой.
не принадлежит прямой.
Задача 13. Написать
уравнение прямой, проходящей через
точку
![]() под углом
под углом
![]() к прямой
к прямой
![]() :
:
![]() .
.
Решение.
Прямая
![]() задана параметрическими уравнениями.
Приведём уравнение прямой
задана параметрическими уравнениями.
Приведём уравнение прямой
![]() сначала к общему виду, а затем к виду
(13). По условию задачи
сначала к общему виду, а затем к виду
(13). По условию задачи
![]() ,
,
![]() .
Подставим данные значения в (11):
.
Подставим данные значения в (11):
![]() ;
;
![]() .
.
Раскрывая скобки и приводя подобные, получаем:
![]() .
.
Таким образом,
![]() .
Подставим значение угла
.
Подставим значение угла
![]() и
и
![]() в формулу (22) для определения
в формулу (22) для определения
![]() :
:
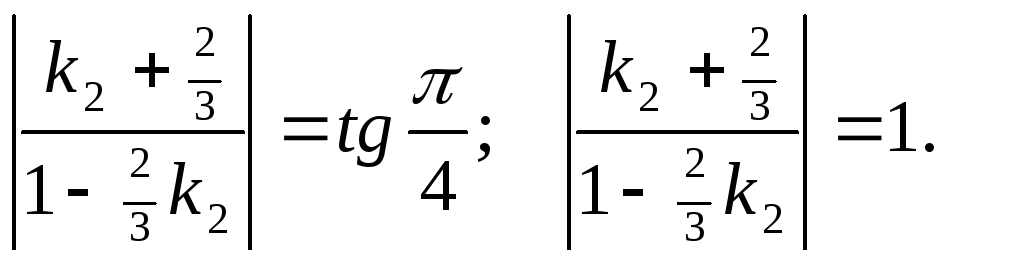
Отсюда:
![]() .
(*)
.
(*)
Для нахождения
![]() необходимо решить уравнение, содержащее
переменную под знаком модуля.
необходимо решить уравнение, содержащее
переменную под знаком модуля.
Рассмотрим 3 случая:
![]() 1)
1)
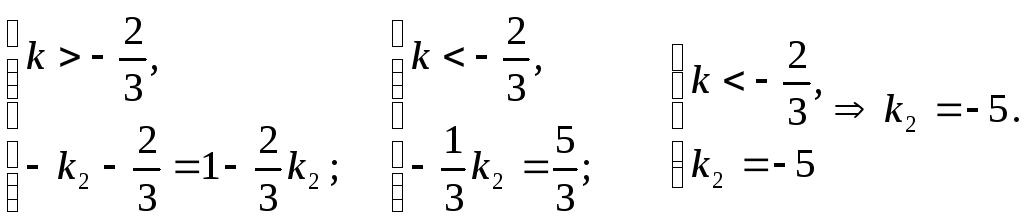
2)
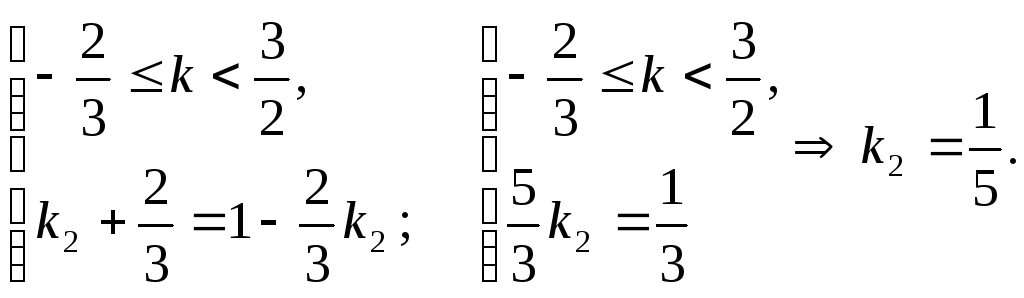
3)
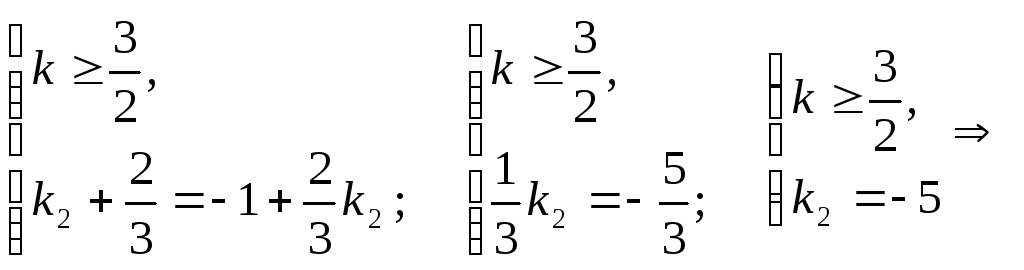 нет
решений.
нет
решений.
Таким образом,
получили 2 значения
![]() ,
которые являются решением данного
уравнения (*):
,
которые являются решением данного
уравнения (*):
![]() или
или
![]() .
.
По условию задачи
прямая проходит через точку
![]() .
Подставим найденные значения
.
Подставим найденные значения
![]() в уравнение (13) и определим значение
в уравнение (13) и определим значение
![]() .
.
1)
![]() :
:
![]() подставим в это уравнение координаты
точки
подставим в это уравнение координаты
точки
![]()
![]()
![]() .
.
Следовательно,
![]() :
:
![]() ;
;
2)
![]() :
:
![]() подставим в это уравнение координаты
точки
подставим в это уравнение координаты
точки
![]()
![]() .
.
Ответ.
![]() или
или
![]() .
.
