31

Министерство образования Российской Федерации

Южно-российский государственный университет экономики и сервиса

(ЮРГУЭС)

Методические указания

к самостоятельной работе по математике

Часть 1

Аналитическая геометрия

для студентов 1 курса всех специальностей

заочной и дистанционной форм обучения

ШАХТЫ 2003

СОСТАВИТЕЛИ

Грозина А.А. доцент кафедры математики, к. т. н.

Саакян О.В. ассистент кафедры математики

Скрипочка Л.Н. ассистент кафедры математики

Хоменко Ю.А. доцент кафедры математики, к.с.н.

РЕЦЕНЗЕНТЫ

Саакян Г.Р. доцент кафедры математики к.т.н.

Охрименко О.И. доцент кафедры математики, к.э.н.

Методические указания предназначены студентам заочной и дистанционной форм обучения для подготовки к сдаче экзаменов, выполнению контрольных работ по дисциплине «Математика». Содержат теоретический материал по теме «Аналитическая геометрия», образцы решения примеров.

Данные методические указания могут быть также использованы и студентами дневной формы обучения при самостоятельном изучении данной темы, при подготовке к сдаче контрольных точек.

СОДЕРЖАНИЕ

Введение 4

1 Аналитическая геометрия 4

1.1 Определители и матрицы 4

Примеры решения задач 6

1.2 Элементы векторной алгебры 8

Примеры решения задач 12

1.3 Прямая на плоскости 17

Примеры решения задач 19

1.4 Уравнения прямой и плоскости в пространстве 24

Примеры решения задач 27

Список использованных источников 31

ВВЕДЕНИЕ

Данные методические указания содержат достаточно большое количество задач с решениями по аналитической геометрии, наиболее часто встречающихся в аудиторных контрольных работах для студентов первого курса заочного факультета всех специальностей.

В данной работе приводятся также теоретические справки по каждому разделу. Приведённая в методических указаниях теоретическая часть позволит использовать их при самостоятельной работе по изучению указанных тем, при подготовке к сдаче экзаменов студентами заочной формы обучения всех специальностей.

В конце методических указаний приводится список рекомендуемой и используемой литературы.

1 Аналитическая геометрия

1.1 ОПРЕДЕЛИТЕЛИ И МАТРИЦЫ

Прежде чем ввести понятие определителя, дадим определение матрицы.

Определение 1. Прямоугольная таблица чисел, состоящая из строк и столбцов, называется матрицей размера . Используется обозначение

,

задающее матрицу размера такую, что на пересечении её той строки и го столбца находится число . В общем виде матрицу размера можно записать таким образом:

.

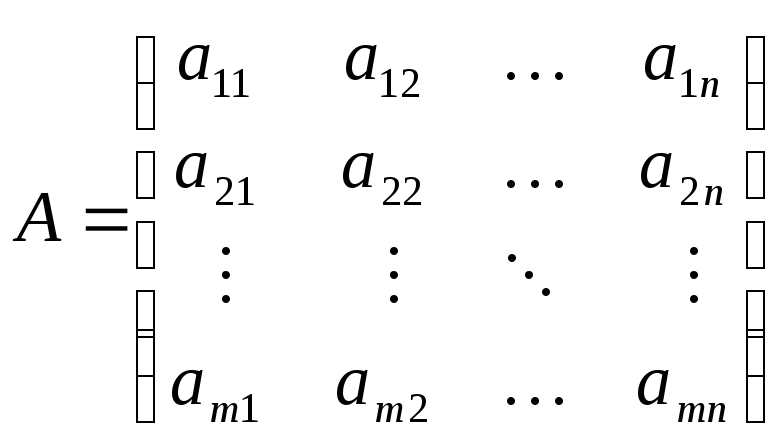Если , т.е. число строк и число столбцов матрицы совпадают, то такая матрица называется квадратной порядка .

Рассмотрим квадратную матрицу второго порядка.

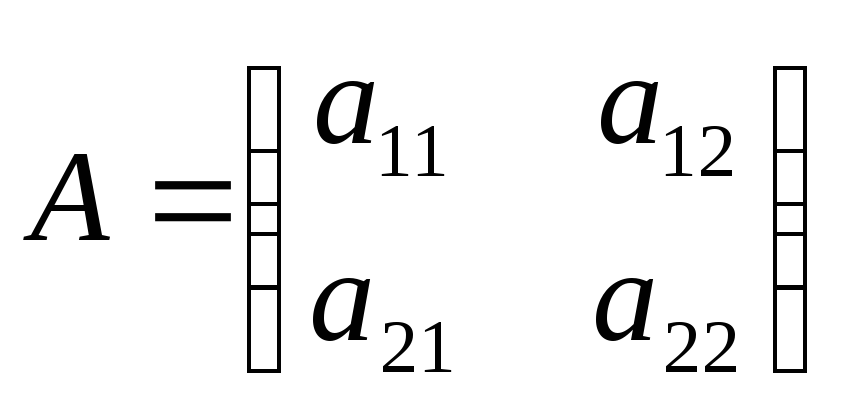
и дадим определение определителя матрицы второго порядка.

Определение 2. Выражение , составленное из элементов матрицы , называется определителем матрицы 2-го порядка (или короче, определителем второго порядка), и обозначается .

. (1)

Дадим теперь понятие определителя третьего порядка (или определителя матрицы размера ).

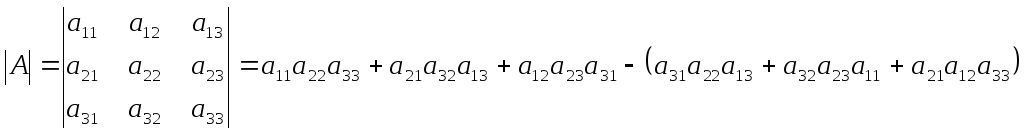. (2)

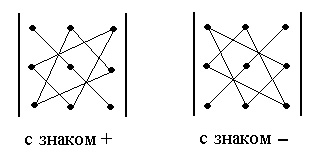
Отметим правило для построения выражения (2). Выделим в этом определителе главную диагональ, образованную числами и диагональ, образованную числами , которую будем называть побочной. Вычисляем произведение элементов, стоящих на главной диагонали и два произведения чисел, расположенных в вершинах двух равнобедренных треугольников с основаниями, параллельными главной диагонали. Складываем эти три произведения. Из полученной суммы вычитаем сумму произведений элементов, стоящих на побочной диагонали и двух произведений чисел, расположенных в вершинах двух равнобедренных треугольников с основаниями, параллельными побочной диагонали.

Рисунок 1

На рисунке 1 это правило изображено схематически.

Рассмотрим теперь определитель го порядка .

.

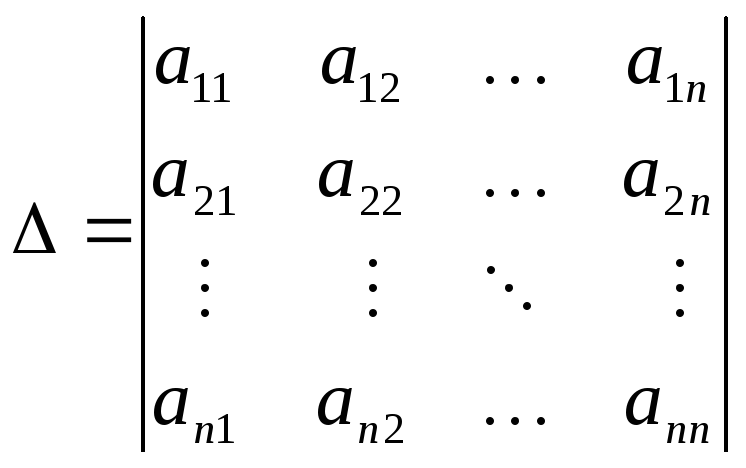Определение 3. Минором любого элемента определителя называется определитель порядка , получающийся из определителя вычёркиванием й строки и го столбца.

Теорема 1. Каков бы ни был номер строки , для определителя го порядка справедлива формула

. (3)

Поэтому все определители порядка можно вычислять по формуле (3), которая представляет собой разложение определителя по элементам ой строки. Аналогичным образом можно записать разложение определителя по элементам го столбца.

. (4)

Следует отметить, что правила (3), (4) выгодно применять, если определитель имеет строку (столбец), в которой лишь небольшое количество элементов отлично от нуля. В этом случае, раскрывая определитель по этой строке (столбцу), мы получим в правой части формул (3), (4) небольшое количество слагаемых.