Учебники / Акуленок М.В. Шикула О.С. Статистическое управление процессами, Контрольные карты управляемости процессов

где Хi - индивидуальные значения в подгруппе; i = 1,2,…,n; Х - среднее подгруппы (в

данном случае значения Х не округляют); n - объем подгруппы.

При выборе масштаба Х -s-карты цена деления шкалы s должна быть такой же, как шкалы Х .

Вычисление положения контрольных границ при незаданных стандартных значениях проводят в соответствии с формулами табл.1.1. Если стандартные значения заданы, расчет положения контрольных границ на Х-карте проводят согласно (2.1) и (2.2). Положение центральной линии соответствует s0 или С4σ0, а положение контрольных границ опреде-

ляется как

UCLs = B5σ0; LCLs = B6σ0.

Оценка статистически управляемого состояния процесса. Для оценки статистиче-

ски управляемого состояния процесса рассчитывают стандартное отклонение I :

I s / С4 , (2.4)

где s - среднее выборочных стандартных отклонений; С4 - делитель, зависящий от объе-

ма подгруппы, значения которого приведены в табл.П2.

Если процесс статистически управляем, имеет нормальное распределение, то полу-

ченное значение стандартного отклонения можно использовать для оценки возможностей процесса по (1.1).

Задача 2.4. Проводится предварительное обследование процесса формирования эмит-

терного слоя. Контролируется поверхностное сопротивление эмиттерного слоя. Измерения проведены по 30 точкам, равномерно распределенным по рабочей поверхности пластины.

По полученным данным, приведенным в табл.2.3, используя АВС-карту, проанализируйте стабильность процесса.

Таблица 2.3

Исходные данные для решения задачи 2.4

Номер точки 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Поверхностное 64 58 37 74 47 46 22 79 62 59 43 44 48 91 55

сопротивление,

Ом/□

Номер точки 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Поверхностное 52 59 46 44 48 53 50 54 78 50 27 21 19 24 39

сопротивление,

Ом/□

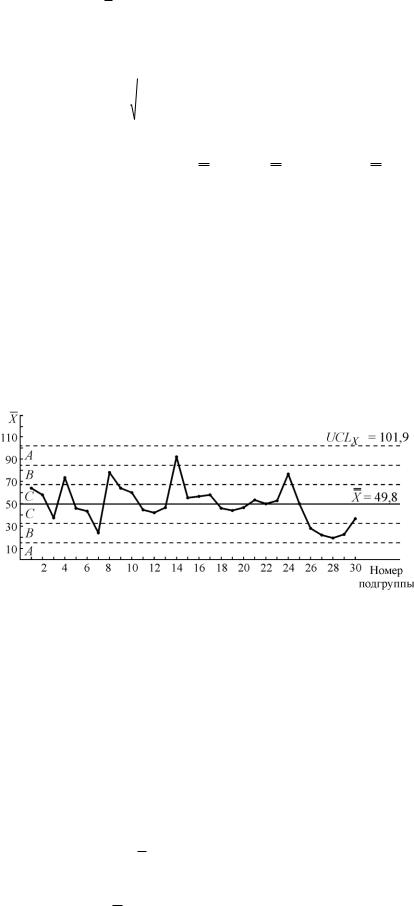
Решение.1. Рассчитываем X и s:

2. Определяем положение центральной линии, верхней и нижней контрольных границ и наносим их на контрольную карту. CL = X , UCL = X + 3s, LCL = X – 3s. Пространство между UCL и LCL делим на шесть зон шириной s.

3. Наносим на карту точки, полученные в результате измерения. Графическая часть карты представлена на рис.2.7.

4. Анализируем карту. На карте, приведенной на рис.2.7, видно, что все точки распо-

лагаются в пределах контрольных границ, однако процесс не находится в статистически управляемом состоянии, так как четыре из пяти точек лежат в зоне В (подгруппы 26 - 30).

Причина такой последовательности должна быть исследована и устранена.

Рис.2.7. Пример применения АВС-карты для решения задачи 2.4

Для статистически неуправляемого процесса расчет индексов воспроизводимости смысла не имеет.

2.3. Контрольная карта медиан и размахов

(Ме-R-карта)

Карты медиан - альтернатива X -R-картам для управления процессом с измеряемыми данными. Они обеспечивают аналогичные выводы, но имеют определенные преимущест-

ва. Карты медиан (Me-R- или X -R-карты) просты в применении и не требуют больших вычислений, так как определение медианы оказывается проще, чем расчет среднего ариф-

метического, хотя их чувствительность к возникновению особых причин вариаций и точ-

ность несколько ниже, чем у X -R-карт. Поскольку Me-R-карта показывает как медиану,

так и разброс, она пригодна для сравнения результатов нескольких процессов или одного процесса до и после проведения мероприятий по совершенствованию процесса. Карта ме-

диан полезна (и даже более объективна) при исследовании процессов, имеющих несиммет-

ричное распределение параметров.

Хотя в целом работа с картами медиан сходна с работой с X -R-картами, однако в ней имеются некоторые особенности.

Сбор данных. Особенности сбора данных для построения карты медиан заключаются в том, что для карт медиан предпочтительны нечетные объемы подгрупп и значения n ≤

10. При этом в блок данных контрольной карты вносят для каждой подгруппы соответст-

венно значения медианы Ме и размаха R.

Построение контрольных карт. Особенности построения карты медиан состоят в следующем:

1) для расчета положения центральной линии находят среднее медиан всех подгрупп

Ме и проводят через эту точку центральную линию на карте. Это значение необходимо также для расчета контрольных границ карты медиан. Кроме среднего медиан подгрупп для определения положения контрольных границ могут быть использованы значения ме-

дианы от медиан подгрупп (расчет средних от медиан подгрупп и средних размахов про-

ще и удобнее);

2)находят среднее размахов R аналогично картам, рассмотренным выше;

3)вычисляют положение верхней и нижней контрольных границ для размахов и ме-

диан по формулам

UCLMe Me A4 R ;

LCLMe Me A4 R ;

UCLR D4 R ;

LCLR D3 R ,

где А4, D4 и D3 - коэффициенты, зависящие от объема подгруппы, значения которых при-

ведены в табл.П2;

4) определяют масштаб осей. В простейшем случае масштаб оси медиан может быть установлен в соответствии со шкалой прибора, измеряющего индивидуальные значения Х.

Если данные не содержат точек, далеко выходящих за пределы установленных границ, то диапазон изменений на карте может быть определен как разность между большим и меньшим индивидуальными измерениями, умноженная на коэффициент от 1,5 до 2;

5) наносят полученные данные на карту.

Возможен и другой подход к построению карты медиан - после определения масшта-

ба оси медиан на карту наносят точки, соответствующие индивидуальным значениям Х для каждой подгруппы по соответствующей вертикальной линии, обводят медиану каж-

дой подгруппы (после чего это значение вносят в блок данных карты) и соединяют медиа-

ны подгрупп линией для выявления трендов.

Оценка статистически управляемого состояния процесса. Оценку статистически управляемого состояния процесса проводят аналогично Х -R-картам. При этом также сравнивают положение каждой точки карты с рассчитанными контрольными границами,

например для части карты, относящейся к размахам (UCLR и LCLR), и выявляют все при-

знаки неслучайного поведения процесса. После идентификации причин такого поведения предпринимают действия для устранения особых причин вариаций, влияющих на размахи

(или медианы).

Необходимое для оценки управляемости процесса стандартное отклонение процесса

I рассчитывают по формуле (2.3). Если процесс имеет нормальное распределение, то полученную оценку стандартного отклонения можно использовать для определения воз-

можностей процесса (см. формулы (1.1)).

Для стабильного процесса с установленными контрольными границами процедура построения карты медиан может быть упрощена. В этом случае используют карточку-

шаблон (например, пластиковую) со шкалой и с уже проведенными центральной линией и контрольными границами (в Ме-зоне карты); работа ведется по подгруппам с выделением всех точек, выходящих за контрольные границы, и соответствующей корректировкой процесса или информированием руководителя (владельца) процесса о выявленных про-

блемах.

Задача 2.5. Для приведенных в табл.2.1 результатов измерений определите значения

Me по подгруппам. Рассчитайте Ме . Постройте карту медиан.

Решение. 1. Определяем значения медиан для всех подгрупп, для чего преобразуем данные табл.2.1 в вариационные ряды (табл.2.4).

2. Определяем положение центральной линии.

Среднее медиан подгрупп Ме = 49,88 Ом/□.

Для сравнения покажем различия двух подходов к работе с картами медиан.

Для определения медианы медиан подгрупп выстраиваем вариационный ряд из полу-

ченных значений медиан подгрупп: 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5

Поскольку в данном ряду четное число элементов, то медиана этого ряда определяет-

ся как среднее между двумя центральными элементами, т.е. медиана медиан подгрупп

MeMe= 48,815 или Ме MeMe .

Такие различия следует учитывать при работе с компьютером.

Таблица 2.4

Определение медиан по подгруппам

3. Определяем масштаб оси медиан: наименьшее индивидуальное значение

Хmin = 48,65 Ом/□, наибольшее Xmax = 51,43 Ом/□. Другими словами, шкала вертикальной оси должна охватить 10 делений (например, от 45 до 55).

4. Определяем положение контрольных границ для R = 1,33 Ом/□ и Ме = 49,88 Ом/□:

UCLMe Me A4 R = 49,88 + 0,69 · 1,33 = 50,8 Ом/□;

LCLMe Me A4 R = 49,88 – 0,69 · 1,33 = 48,96 Ом/□;

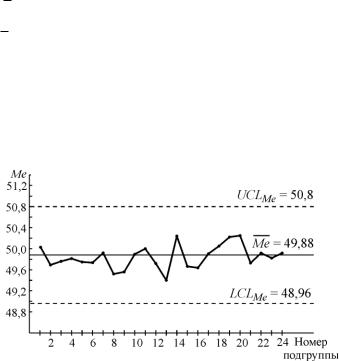
UCL120 = D4 R120 = 2,124 · 1,3 = 2,76 Ом/□; LCL120 = D3 R120 = 0 · 1,3 = 0.

5. Построенный график медиан (рис.2.8) не содержит признаков действия особых причин вариаций, однако делать вывод о стабильности или нестабильности процесса ре-

комендуется только после анализа R-части карты.

Рис.2.8. Пример построения карты медиан (к решению задачи 2.5)

2.4.Контрольная карта индивидуальных значений

искользящих размахов (Х-МR-карта)

Внекоторых ситуациях для управления процессом невозможно организовать работу с подгруппами. Обычно это происходит, когда:

-измерения дорогостоящие;

-измерения осуществляются в условиях разрушающего контроля;

-невозможно получить более одного значения показателя качества;

-промежуток времени между измерениями велик.

Во всех перечисленных ситуациях приходится управлять процессом на основе инди-

видуальных значений, при этом полезно использовать X-MR-карту.

Главная особенность X-MR-карт заключается в том, что при работе с индивидуальны-

ми значениями показателя качества размах внутри подгруппы фактически равен нулю. В

таких случаях используют значения скользящих размахов MR, определяемые, например,

как разность измерений в последовательных парах, т.е. разность первого и второго изме-

рений, затем второго и третьего и т.д.

При использовании карт индивидуальных значений необходимо учитывать следую-

щее:

- карты индивидуальных значений не столь чувствительны к изменениям процесса,

как X - и R-карты;

- если распределение процесса не является нормальным (например, несимметрично),

следует проявлять осторожность при интерпретации карт индивидуальных значений;

- карты индивидуальных значений не позволяют оценить воспроизводимость процес-

са от изделия к изделию, поэтому, если это возможно, следует использовать X - и R-карты с малыми объемами выборочных подгрупп (от 2 до 4), даже если это приведет к увеличе-

нию интервала между подгруппами.

Сбор данных. При сборе данных для Х-MR-карты необходимо обратить внимание на следующее:

- индивидуальные значения Х в блоке данных X-MR-карты записывают слева направо

(в строку), а не по подгруппам сверху вниз, как на рассмотренных выше Х -R-картах;

- скользящий размах MR между индивидуальными значениями вычисляют, как прави-

ло, как разность между каждой последовательной парой измерений. Таких значений раз-

ности будет на одно меньше, чем измерений (20 измерений дают 19 значений MR).

В общем случае значение MR может быть рассчитано на основе подгруппы фиксирован-

ного объема (в том числе трех-четырех измерений).

Построение контрольных карт. Для построения Х-MR-карты прежде всего опреде-

ляют положение контрольных границ. Контрольные границы вычисляют в соответствии с формулами табл.1.1 с учетом значений среднего скользящего размаха MR и среднего по

всем рассмотренным подгруппам X .

Построение Х-карты ведут аналогично построению Х -R-карты. Средний скользящий размах MR вычисляют по полученным значениям MR аналогично вычислению среднего размаха в вышеприведенных алгоритмах.

Масштаб осей Х-MR-карты определяют аналогично карте медиан: если нет точек, да-

леко выходящих за пределы установленных границ, диапазон изменений, отраженный на карте, может быть определен как разность между большим и меньшим индивидуальными измерениями, умноженная на коэффициент от 1,5 до 2. Масштаб в зоне MR-карты реко-

мендуется выбирать такой же, как и в зоне Х-карты.

Положение контрольных границ определяют как

UCLМR D4 MR ;

LCLМR D3 MR ;

UCLX X E2 MR ;

LCLX X E2 MR ,

где MR - средний скользящий размах; Х - среднее процесса; D4, D3, E2 - множители, завися-

щие от объема подгруппы n, которые приведены в табл.П2. Данные коэффициенты при вы-

числении скользящего размаха как разности между соседними индивидуальными значе-

ниями определяются для n = 2.

При заданных стандартных значениях положение центральной линии на Х-карте оп-

ределяют как Х0, положение контрольных границ рассчитывают как

UCLХ = Х0 + 3σ0;

LCLХ = Х0 3σ0.

Для карты скользящих размахов положение контрольных границ при заданных стан-

дартных значениях определяют как

UCLMR = D2σ0;

LCLMR = D1σ0.

Оценка статистически управляемого состояния процесса. Оценку управляемости процесса проводят в соответствии с описанным выше обобщенным алгоритмом. Для этого исследуют карту скользящих размахов на предмет наличия точек за пределами контроль-

ных границ и других признаков неслучайного поведения процесса (см. рис.1.6). При этом следует учитывать, что вероятность ошибки первого рода для данного типа карт выше.

Так, несимметричное распределение процесса может демонстрировать признаки особых

причин, когда на самом деле они не существуют.

Для оценки управляемости процесса используют значение стандартного отклоненияI , рассчитанное по формуле (2.3). Если подтверждена статистическая управляемость процесса, оценку возможностей процесса проводят в соответствии с (1.1).

Задача 2.6. Постройте карту скользящих размахов для данных, приведенных в

табл.2.3.

Решение. Определяем средний скользящий размах по скользящим размахам, приве-

денным в табл.2.5: MR = 15,5 Ом/□.

Таблица 2.5

Определение скользящего размаха

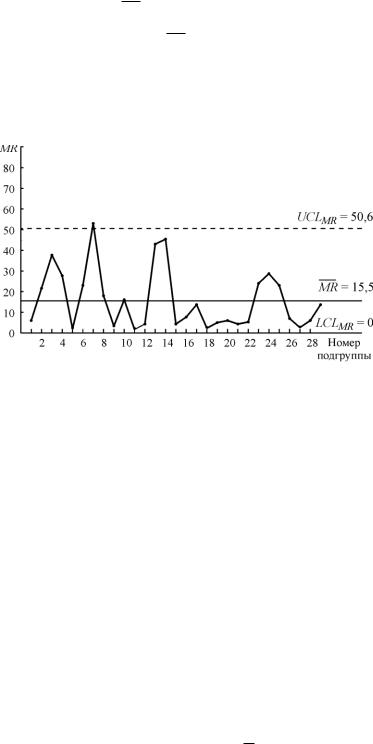
Рассчитываем положение контрольных границ на карте размахов. При определении значений коэффициентов D4 и D3 учитываем, что n = 2:

UCLМR D4 MR = 3,267 · 15,5 = 50,6 Ом/□;

LCLМR D3 MR = 0 · 15,5 = 0.

Карта скользящих размахов приведена на рис.2.9. Следует отметить наличие точки,

выходящей за контрольные границы.

Рис.2.9. Пример построения карты скользящих размахов (к решению задачи 2.6)

Задачи

Задача 2.7. По количественным данным для процесса формирования скрытого слоя,

приведенным в табл.2.2, постройте Me-R-карты. Сравните полученные результаты с КК на рис.2.7.

Задача 2.8. По данным табл.2.3 постройте Х-MR-карту. Сравните полученные резуль-

таты с КК на рис.2.8.

Задача 2.9. Проводится мониторинг процесса выращивания высокоомных слоев кремния,

одним из показателей качества которого является удельное сопротивление выращенного слоя. Среднее значение удельного сопротивления должно составлять 150 15 Ом см. Качест-

во оценивается по 10 пластинам. Измерения проводятся на каждой пластине в 5 точках. Ре-

зультаты измерений приведены в таблице. Постройте Х -R-карту. Определите, находится ли процесс в статистически управляемом состоянии. Рассчитайте индексы воспроизводимости процесса и определите долю брака.

Задача 2.10. Проводится мониторинг процесса осаждения эпитаксиального слоя p-

типа, одним из показателей качества которого является удельное сопротивление выра-

щенного слоя. Среднее значение удельного сопротивления должно составлять 15 1,5

Ом см. Качество оценивается по 10 пластинам. Измерения проводятся на каждой пластине в 5 точках. Результаты измерений приведены в таблице. Постройте Х -R-карту. Определи-

те, находится ли процесс в статистически управляемом состоянии. Рассчитайте индексы воспроизводимости процесса и определите долю брака.

Задача 2.11. При проведении процесса формирования подзатворного диэлектрика од-

ним из показателей качества процесса является толщина диэлектрика, которая должна со-

ставлять 0,15 0,15 мкм. Качество оценивается по 10 пластинам. Измерения проводятся на каждой пластине в 5 точках. Результаты измерений приведены в таблице. Постройте Х- R-карту. Определите, находится ли процесс в статистически управляемом состоянии. Рас-

считайте индексы воспроизводимости процесса и определите долю брака.

Задача 2.12. Используя данные задачи 2.11, постройте Me-R-карту. Сравните полу-

ченные результаты.