
Учебники / Акуленок М.В. Шикула О.С. Статистическое управление процессами, Контрольные карты управляемости процессов
.pdf
I R / d2 , (2.3)
где R - средний размах подгрупп (для периодов с размахами процесса в управляемом со-
стоянии);
- с учетом нового значения n объема подгруппы определить новые значения D3, D4, А2
(см. табл.П2);
- рассчитать новые значения размаха и положения контрольных границ:
Rнов I d2 ;
UCLR D4 Rнов ;
LCLR D3 Rнов ;
UCLX X A2 Rнов ;
LCLX X A2 Rнов ;
- нанести на контрольные карты новые границы для оценки текущего состояния про-
цесса.
При последующем мониторинге процесса появление сигнала об изменении среднего или размаха процесса требует установить причину, и если выявленное изменение подтверждено, положение контрольных границ следует снова пересчитать.
Оценка возможностей процесса. Если установлено, что процесс находится в стати-
стически управляемом состоянии, то оценивают возможности процесса по стабильному выполнению технических требований. Для этого рассчитывают индексы воспроизводимо-
сти по одной из формул (1.1).
Задача 2.1. Проводится предварительное обследование технологического процесса формирования скрытого слоя. Одним из показателей процесса является величина поверх-
ностного сопротивления (Ом/□). Контроль проводится по пяти точкам на каждой пласти-
не. Результаты измерений поверхностного сопротивления приведены в табл.2.1. Построй-
те Х -R-карту и сделайте вывод о состоянии процесса.
Решение. 1. Поскольку на каждой пластине проведено пять измерений, то подгруппы могут быть сформированы из этих пяти измерений на каждой пластине. Определяем сред-
нее X и размах R по подгруппам, значения этих параметров заносим в блок данных кон-
трольной карты.
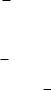
Таблица 2.1
Результаты измерений поверхностного сопротивления скрытого слоя (Ом/□)
|
Номер |
|
|
|
|
|
|
|
|
|
Номер пластины (подгруппы) |
|
|
|
|||||||||||||
|
измерения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
|
|
4 |
|
5 |
|
|
|
6 |
|
7 |
8 |
9 |
10 |
11 |
12 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Х1 |
49,15 |
49,71 |
49,77 |
49,84 |
50,96 |
49,53 |
50,21 |
50,70 |
48,65 |
49,44 |
49,74 |
50,31 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Х2 |
50,85 |
50,47 |
49,09 |
50,68 |
49,74 |
49,95 |
50,00 |
49,01 |
49,64 |
49,94 |
49,53 |
49,79 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Х3 |
50,09 |
48,92 |
50,27 |
49,76 |
49,53 |
49,76 |
50,76 |
49,42 |
49,58 |
50,53 |
50,83 |
49,89 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Х4 |
49,80 |
50,29 |
49,38 |
51,11 |
49,45 |
50,09 |
49,75 |
49,53 |
50,65 |
49,32 |
50,15 |
49,31 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Х5 |
50,33 |
49,26 |
50,35 |
49,21 |
50,02 |
48,91 |
49,28 |
50,34 |
50,25 |
51,43 |
50,21 |
49,30 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер |
13 |
14 |
|
15 |
|
|
16 |
|
17 |
|
|
18 |
|
19 |
20 |
21 |
22 |
23 |
24 |
|||||||
|
измерения |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Х1 |
49,99 |
49,13 |
50,37 |
49,38 |
50,22 |
50,13 |
49,91 |
50,30 |
49,25 |
50,22 |
48,90 |
50,24 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Х2 |
49,70 |
50,30 |
49,47 |
49,97 |
49,92 |
49,98 |
49,81 |
50,28 |
50,12 |
50,50 |
49,66 |
49,94 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Х3 |
49,16 |
50,11 |
49,35 |
49,77 |
49,83 |
49,85 |
50,45 |
50,20 |
49,79 |
49,90 |
49,84 |
50,06 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Х4 |
49,44 |
50,36 |
50,19 |
50,65 |
50,82 |
50,60 |
50,26 |
50,59 |
49,72 |
48,72 |
50,32 |
51,13 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Х5 |
49,11 |
50,80 |
49,76 |
49,75 |
49,79 |
50,39 |
50,29 |
49,63 |
50,90 |
49,46 |
49,48 |
49,69 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Определяем среднее X120 и средний размах |
R |
120 по 24 подгруппам: |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
= 49,93 Ом/□; |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
X120 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
= 1,3 Ом/□, |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
120 |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где k = 24 - количество подгрупп; индекс «120» соответствует объему проанализирован-
ной выборки.
3. Определяем положение центральной линии для R-карты:
R120 = 1,33 Ом/□.
Рассчитываем положение контрольных границ:
UCL120 = D4 R120 = 2,124 · 1,3 = 2,76 Ом/□;
LCL120 = D3 R120 = 0 · 1,3 = 0.
В зоне размахов контрольной карты отмечаем центральную линию, UCL и LCL, нано-
сим точки, соответствующие размахам каждой подгруппы и соединяем их линиями.
Графическая часть контрольной карты приведена на рис.2.1.

Рис.2.1. Пример графической части Х -R-карты без заданных стандартных значений (к решению задачи 2.1)
4. Определяем положение центральной линии для X -карты:
X = 49,93 Ом/□.
Рассчитываем положение контрольных границ:
UCL = X + A2 R = 49,93 + 0,577 · 1,3 = 50,68 Ом/□;
LCL = X – A2 R = 49,93 – 0,577 · 1,3 = 49,18 Ом/□.
ВХ -зоне графической части контрольной карты отмечаем центральную линию, UCL
иLCL, наносим точки, соответствующие средним каждой подгруппы, и соединяем их ли-
ниями (см. рис.2.1).
5. Анализируем построенную карту:
-все значения R находятся внутри контрольных границ, других признаков действия особых причин вариаций не обнаружено;
-точки X -карты не выходят за пределы контрольных границ, других сигнальных при-
знаков на карте также не обнаружено.
Данная ситуация требует дополнительного исследования, поскольку может быть свя-
зана с некорректным планом сбора данных.
Задача 2.2. Проанализируйте данные табл.2.1 и постройте Х -R-карту при заданных стандартных значениях. Поверхностное сопротивление скрытого слоя должно составлять 50
± 1,5 Ом/□, т.е. Х0 = 50 Ом/□ и σ0 = 0,5. Сделайте вывод о состоянии процесса.
Решение. 1. Определяем среднее X и размах R по подгруппам, значения этих пара-
метров заносим в соответствующие графы контрольной карты (блок данных).
2. Для X -карты:
- положение центральной линии: X 0 = 50 Ом/□;
- положение контрольных границ:
UCLX = X 0 +А1 σ0 = 50 + 1,342 · 0,5 = 50,671 Ом/□;
LCLX = X 0 – А1 σ0 = 50 – 1,342 · 0,5 = 49,329 Ом/□.
3. Для R-карты:
-положение центральной линии: R = d2σ0 = 2,326 · 0,5 = 1,163 Ом/□;
-положение контрольных границ:
UCLR = D2σ0 = 4,918 · 0,5 = 2,459 Ом/□;
LCLR = D1σ0 = 0 · 0,5 = 0.
В зоне размахов контрольной карты отмечаем центральную линию, UCL и LCL, нано-
сим точки, соответствующие размахам каждой подгруппы, и соединяем их линиями.
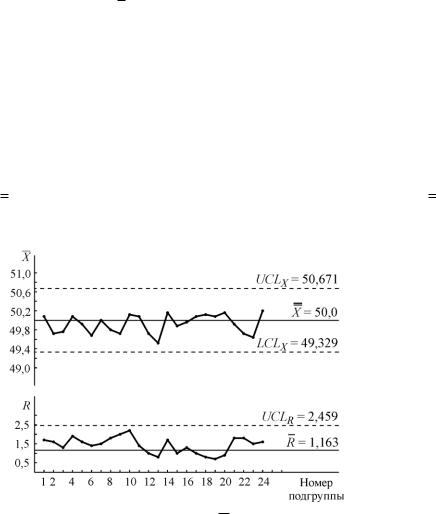
Графическая часть контрольной карты показана на рис.2.2.
4. Сравниваем X = 50,0 Ом/□ с рассчитанным в предыдущей задаче средним X = 49,93
Ом/□.
Рис.2.2. Пример графической части Х -R-карты с заданными стандартными значениями (к решению задачи 2.2)
В Х-зоне контрольной карты отмечаем центральную линию, UCL и LCL, наносим точ-
ки, соответствующие средним каждой подгруппы, и соединяем их линиями (см. рис.2.2).
5. Анализируем полученную карту:
- все значения R находятся внутри контрольных границ, однако имеется особая конфигу-
рация точек - более восьми точек подряд выше центральной линии (подгруппы 1 - 10). Это позволяет сделать вывод, что R-карта указывает на появление особых причин вариаций и возможный переход в статистически неуправляемое состояние процесса. Однако это может быть признаком смены измерительной системы и требует дополнительного анализа. Данная ситуация требует исследования и идентификации выявленных причин отклонения и после-
дующей разработки КД;

- все точки X -карты не выходят за пределы контрольных границ, других сигнальных признаков на карте также не обнаружено.
Задача 2.3. Проводится анализ технологического процесса формирования подзатвор-
ного диэлектрика методом сухого термического окисления. Основным показателем подза-
творного диэлектрика является его толщина, которая должна составлять 0,125 - 0,219 мкм.
Используя результаты измерений 20 подгрупп (табл.2.2), постройте Х -R-карту и опреде-
лите, стабилен ли процесс.
Таблица 2.2
Результаты измерений толщины оксида
Номер |
|
|
|
|
Номер подгруппы |
|
|
|
|||
измерения |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Х1 |
0,189 |
0,201 |
0,221 |
0,183 |
0,169 |
0,162 |
0,200 |
0,240 |
0,199 |
0,178 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Х2 |
0,172 |
0,191 |
0,219 |
0,181 |
0,226 |
0,183 |
0,193 |
0,182 |
0,198 |
0,171 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Х3 |
0,206 |
0,187 |
0,207 |
0,196 |
0,206 |
0,191 |
0,216 |
0,191 |
0,207 |
0,182 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Х4 |
0,189 |
0,192 |
0,198 |
0,180 |
0,209 |
0,178 |
0,208 |
0,226 |
0,202 |
0,196 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер |
11 |
12 |
13 |
14 |
|
15 |
16 |
17 |
18 |
19 |
20 |
измерения |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х1 |
0,216 |
0,192 |
0,176 |
0,192 |
0,192 |
0,172 |
0,182 |
0,181 |
0,170 |
0,169 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Х2 |
0,174 |
0,198 |
0,198 |
0,187 |
0,199 |
0,194 |
0,179 |
0,158 |
0,156 |
0,166 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Х3 |
0,196 |
0,237 |
0,224 |
0,190 |
0,212 |
0,211 |
0,187 |
0,169 |
0,169 |
0,170 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Х4 |
0,192 |
0,200 |
0,202 |
0,198 |
0,216 |
0,232 |
0,182 |
0,168 |
0,170 |
0,160 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. 1. Определяем среднее X и размах R по подгруппам, значения этих пара-
метров заносим в соответствующие графы контрольной карты.
2. Определяем среднее X и средний размах R для k = 20 :
X 80 X = 0,192 мкм;
k
R80 R = 0,029 мкм.
k
3. Для R-карты:
-положение центральной линии: R = 0,029 мкм;
-положение контрольных границ:
UCLR = D4 R = 2,282 · 0,029 = 0,066 мкм;
LCLR = D3 R = 0 · 0,029 = 0.
В зоне размахов контрольной карты отмечаем центральную линию, UCLR и LCLR, на-
носим точки, соответствующие размахам каждой подгруппы, и соединяем их линиями.
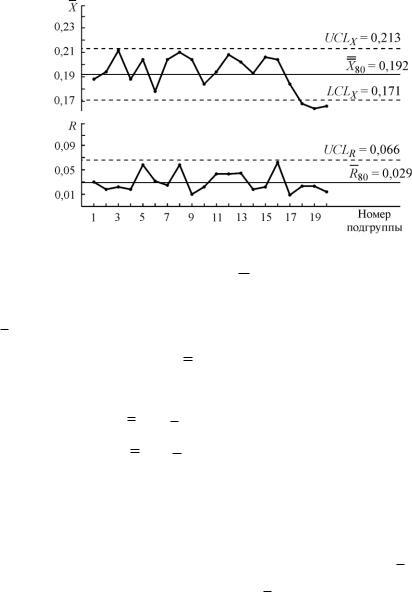
Графическая часть контрольной карты приведена на рис.2.3. Полный вид данной кон-
трольной карты представлен на рис.2.4.
Анализируем полученную карту. Поскольку все значения R находятся внутри кон-
трольных границ и особые структуры отсутствуют, делаем вывод, что R-карта указывает на статистически управляемое состояние процесса.
Рис.2.3. Пример графической части Х -R-карты (к решению задачи 2.3)
4. Для X -карты:
-положение центральной линии: X = 0,192 мкм;
-положение контрольных границ:
UCLX = X + A2 R = 0,192 + 0,729 · 0,029 = 0,213 мкм;
LCLX = X – A2 R = 0,192 – 0,729 · 0,029 = 0,171 мм.
В Х-зоне контрольной карты отмечаем центральную линию, UCLX и LCLX, наносим точки, соответствующие среднему в каждой подгруппе, и соединяем их линиями (см.
рис.2.3 и 2.4).
Анализируем полученную карту. Поскольку последние три точки X выходят за пределы нижней контрольной границы, делаем вывод, что X -карта указывает на возможность дейст-
вия особых причин вариаций.
5.Выявляем действующие особые причины, проводим корректирующие действия для устранения особых причин и предотвращения их повторения.
6.Для дальнейшего анализа КК исключаем точки, вышедшие за контрольные грани-
цы. Из блока данных исключаем все соответствующие подгруппы.
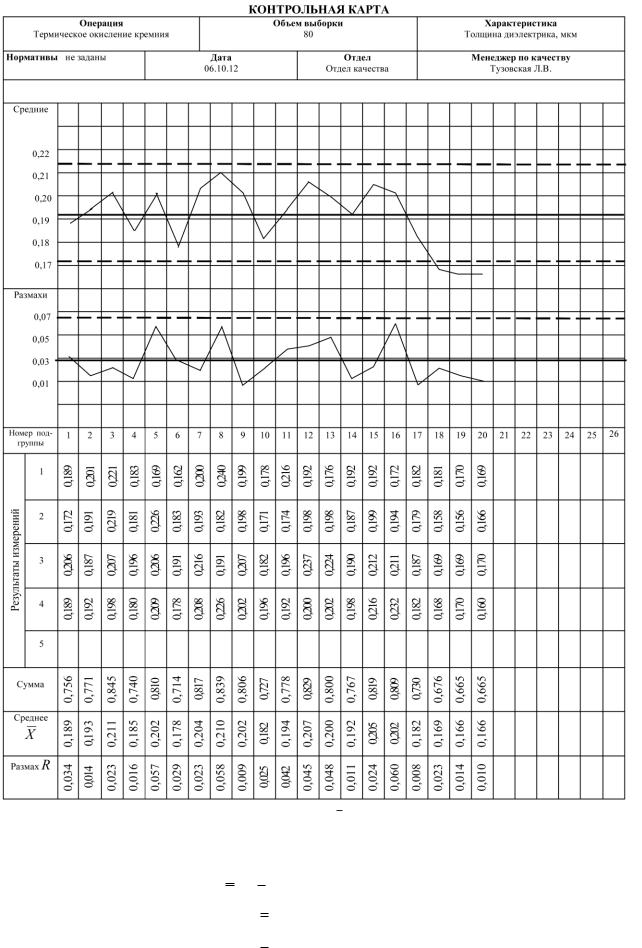
Рис.2.4. Пример X- R-карты
7. Пересчитываем положение контрольных границ (для оставшихся 17 подгрупп).
Вычисляем новые значения X и R :
X 68 = 0,191 мкм;
R68 = 0,031 мкм.
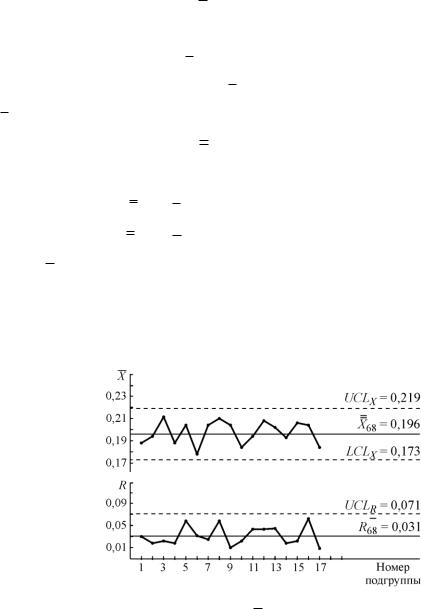
Для R-карты рассчитываем:
-положение центральной линии: R = 0,031 мкм;
-положение новых контрольных границ:
UCLR = D4 R = 2,282 · 0,031 = 0,071 мкм;
LCLR = D3 R = 0 · 0,031 = 0.
Для X -карты определяем:
-положение центральной линии: X = 0,196 мкм;
-положение новых контрольных границ:
UCLX = X + A2 R = 0,196 + 0,729 · 0,031 = 0,219 мкм;
LCLX = X – A2 R = 0,196 – 0,729 · 0,031 = 0,173 мкм.
8. Строим X - и R-карты с новым положением границ и сокращенным числом под-
групп.
Графическая часть данной карты приведена на рис.2.5.
Рис.2.5. Вид графической части X -R-карты, приведенной на рис.2.3, после пересчета контрольных границ (к решению задачи 2.3)
Полный вид контрольной карты представлен на рис.2.6.
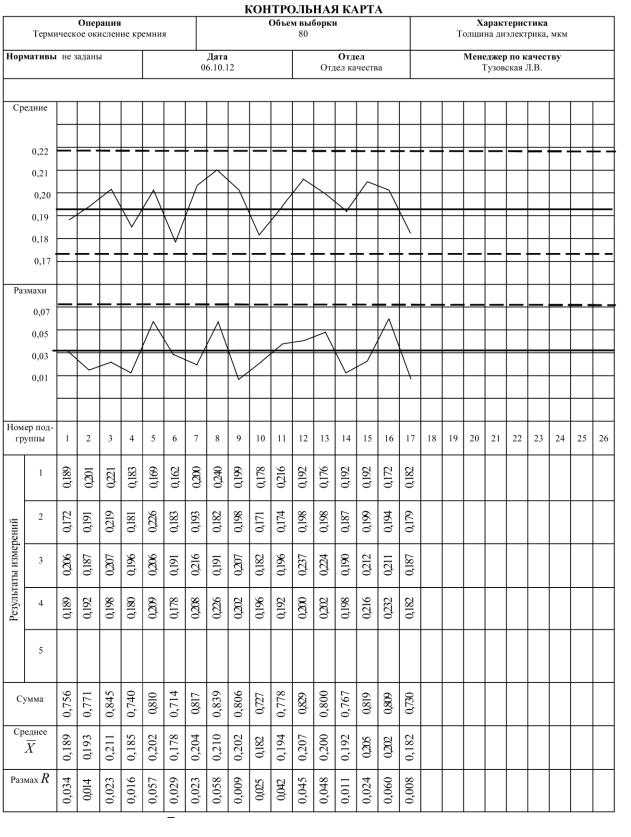
Рис.2.6. Пример X-R-карты, приведенной на рис.2.4, после пересчета контрольных границ
9. Анализируем полученную карту. На этой карте (см. рис.2.5 и 2.6) отсутствуют при-
знаки действия особых причин вариаций.

Процесс находится в статистически управляемом состоянии. Для такого процесса можно рассчитать собственную изменчивость и определить индексы воспроизводимости
Ср , Cpk по формулам (1.1):
|
Cp |
0,21 0,12 |
1,0; |
|
||
|
6 0,015 |
|
||||
|
|
|
|
|||
Сpk = min{ |
0,219 0,196 |
; |
0,196 0,173 |
}= 0,51. |
||
|
3 0,015 |
3 0,015 |
|
|||
Возможности процесса можно было бы считать приемлемыми (Ср = 1,0), однако процесс не центрирован Сpk < Cp. На практике это может привести к высокому проценту бракованных изделий. Необходимо прежде всего центрировать процесс, поддерживая его
встатистически управляемом состоянии.
2.2.Контрольная карта средних арифметических
истандартных отклонений ( X -s-карта)
Карты Х -s, как и Х -R-карты, построенные по измеренным (количественным) данным,
полученным на выходе процесса, являются парными. Однако карты размахов применяют чаще, поскольку размах легко вычислить, и этот вариант карты более точен при малых объемах подгрупп (< 9).
Выборочное стандартное отклонение sI - более точный показатель изменчивости про-
цесса, особенно при больших объемах выборки. Однако его сложнее вычислить, и оно ме-
нее чувствительно к возникновению особых причин изменчивости. Обычно s-карты при-
меняют вместо R-карт, если данные оперативно обрабатываются (например, в
автоматическом режиме, компьютером, включая вычисления s), либо при использовании больших объемов выборок.
Сбор данных осуществляют в соответствии c рассмотренным выше алгоритмом с уче-
том некоторых отличий. Например, если измеренных данных много, их значения вносят в отдельную таблицу, на самой карте (в блоке данных) отмечают только значения Х и s для подгрупп.
Построение контрольных карт. Выборочное стандартное отклонение для каждой под-
группы вычисляют по одной из следующих формул:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X i |
|
|
|
2 |
|
|
|
|
|
||
|
|
|
sI |
X |
|
|
|
|
|
||||||||||
|
|
|
|
|
n 1 |
; |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
X i2 |
n |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
sI |
X |
|
|
|
|
X12 |
X 22 |
... X n2 n |
X |
2 |
|
, |
|||||||
n |
1 |
|
|
|
|
|
n 1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
