10. Кинетическая энергия. Формулы для определения кинетической энергии движущегося твердого тела (при поступательном, вращательном, плоскопараллельном движениях). Единицы измерения.

В билетах_____________

Кинетическая энергия – скалярная величина равная произведению массы на квадрат скорости точки пополам.

Кин энергия мех системы – сумма кинетических энергий всех ее точек (Джоули)

при поступательном

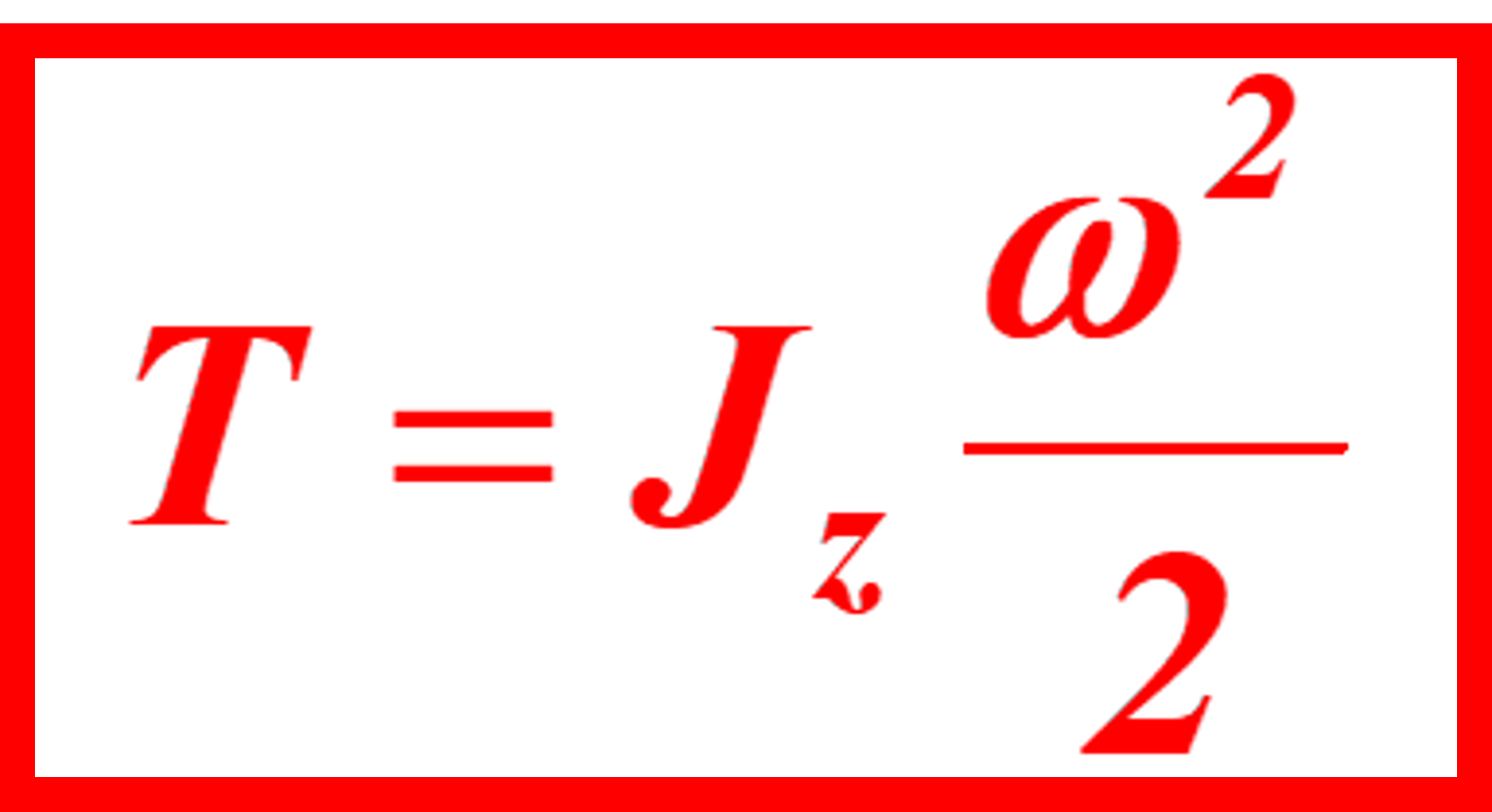при вращательном

при плоскопараллельном

При плоском движении твердого тела кинетическая энергия складывается из кинетической энергии поступательного движения вместе с центром масс и кинетической энергии от вращения вокруг оси, проходящей через центр масс, перпендикулярно плоскости движения тела

11. Теорема об изменении кинетической энергии точки и механической системы. Доказательство теоремы.

В билетах_____________

Изменение кинетической энергии точки произошедшее на каком-либо перемещении равно сумме работ внешних и внутренних сил, на том же перемещении.

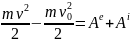
Доказательство:

12. Количество движения материальной точки, определение, единицы измерения. Количество движения в проекциях на координатные оси.

В билетах_____________

Количеством движения материальной точки называют вектор, равный произведению массы системы на скорость центра масс q = Vцентр масс*m

13. Количество движения механической системы, определение, единицы измерения. Количество движения механической системы в проекциях на координатные оси.

В билетах_____________

Количеством движения системы называют векторную сумму количеств движения точек, входящих в систему

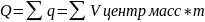
14. Теорема об изменении количества движения. Доказательство теоремы. Элементарный и полный импульс силы. Размерность.

В билетах_____________

Изменение количества движения мех системы произошедшее за некоторое время равно сумме импульсов внешних сил за это время

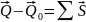
Доказательство:

*Берем определенные интегралы с переменным верхним пределом для того, чтобы не находить постоянные интегрирования

Действие силы F на материальную точку в течении времени dt можно охарактеризовать элементарным импульсом силы:

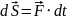
п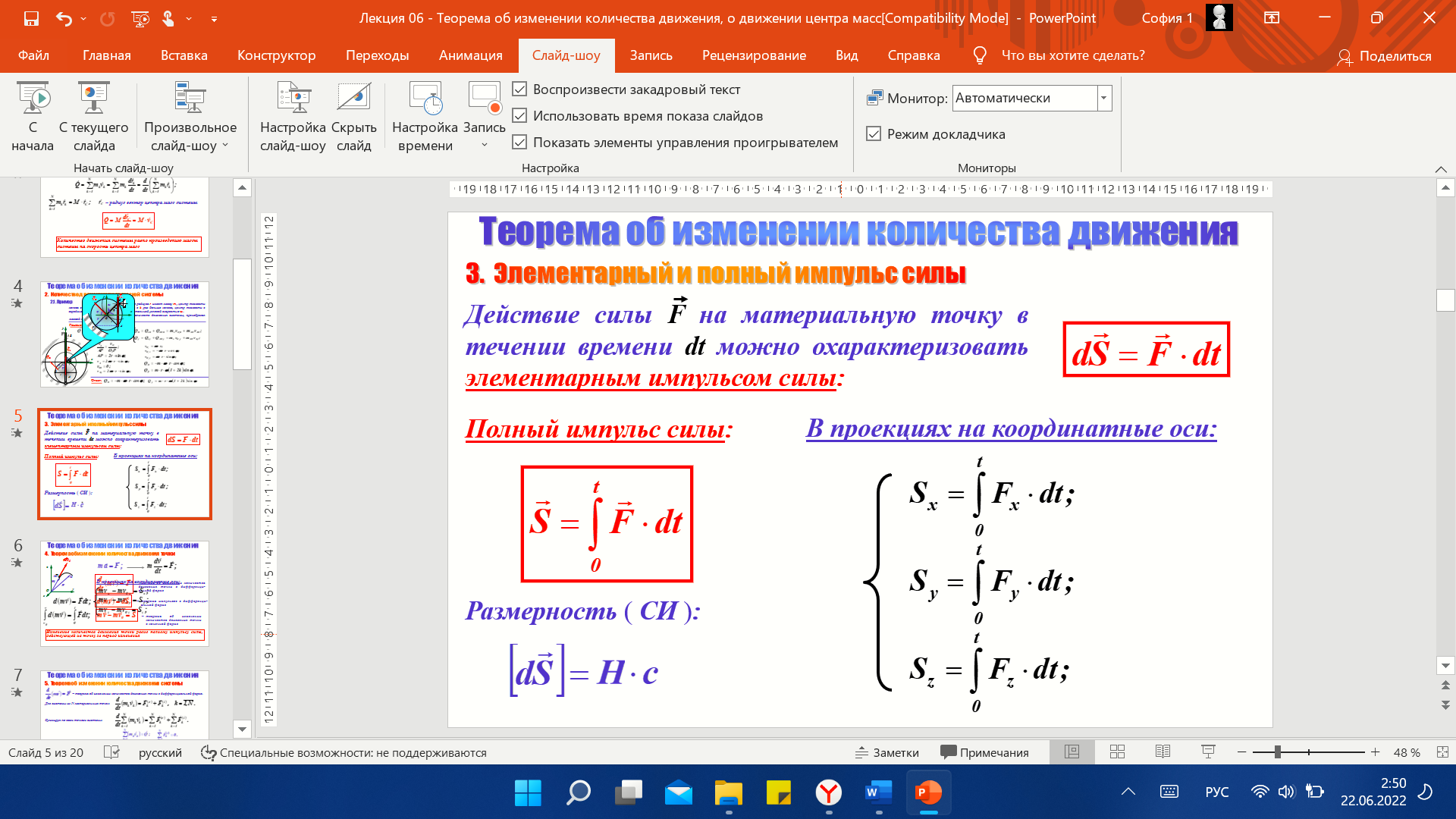 олный импульс силы – предел, к которому стремится сумма элементарных импульсов при стремлении к нулю каждого из промежутков времени dt (интеграл от силы по времени)

15. Закон сохранения количества движения для материальной точки и механической системы. Доказательство. Проекции на координатные точки.

В билетах_____________

Это не закон, а следствие из теоремы об изменении количества движения: «Если главный вектор внешних сил равен 0, то кол-во движения величина постоянная»

Д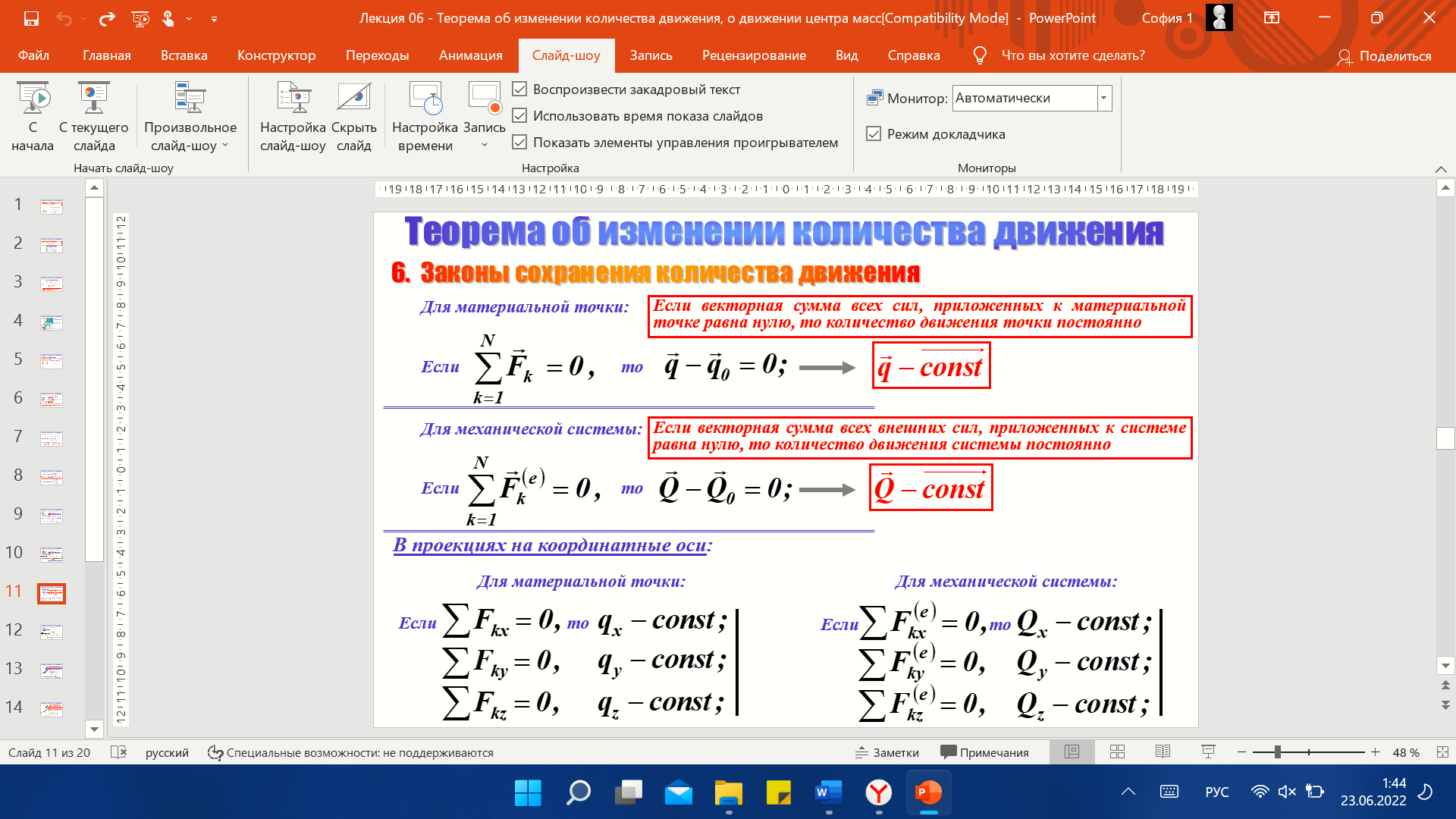 ля точки: «Если векторная сумма всех сил, приложенных к материальной точке равна нулю, то количество движения точки постоянно»

Для системы: «Если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянным по направлению и по модулю»

Если F = 0, то и S=0, следовательно Q и Q₀ равны

16. Принцип возможных перемещений. Понятие возможного перемещения. Условие применения.

В билетах_____________

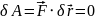
Для равновесия механической системы с удерживающими, идеальными, голономными и стационарными связями необходимо и достаточно, чтобы сумма элементарных работ всех активных (внешних) сил, действующих на систему, на любых возможных перемещениях системы равнялась нулю.

Понятие возможного перемещения – это воображаемые, бесконечно малое перемещение, которое она может получить в данный момент времени из данного положения, допускаемое связями, существующими в этой системе.

Пример: система находится в равновесии и нужно найти неизвестную силу

Условие: система идеальна; сумма работ активных сил равна 0.