Поскольку для однородной жидкости, согласно формуле (1.17)

В уравнении (1.55) константа отброшена по причине того, что она, также как и функция f(t), включена в потенциал. После вычисления потенциала из уравнения (1.55) найдем давление p.

1.3.5Установившееся плоское движение сжимаемой жидкости (газа).

1.3.6Неустановившееся одномерное течение.

Одномерные течения отличаются тем, что все величины определяющие такой поток зависят от одной пространственной переменной и от времени.

Одномерное течение может быть прямолинейным или же криволинейным. Примерами криволинейных одномерных течений являются радиальные цилиндрические и сферические течения в бесконечной среде, а также течения в криволинейных трубах.

Основным предположением при построении теории одномерных течений жидкостей в трубах является гипотеза плоских сечений. Смысл этой гипотезы состоит в том,что скорость течения, давление и плотность в сечении перпендикулярном оси трубы являются неизменными по сечению величинами и изменяются от сечения к сечению. В этом случае из уравнения неразрывности в интегральной форме вытекает закон постоянства расхода жидкости по сечению трубы.

Пример течения в трубе переменного сечения рассмотрен ниже (стр. ??). Теория одномерных течений подробно изложена, например, в монографиях [3], [4].

1.4Примеры решения простейших задач гидро и газо динамики с применением интеграла Бернулли.

Во всех задачах будем рассматривать течение однородной несжимаемой жидкости. Иначе говоря во все моменты времени % = %0 = const: В этом случае уравнение неразрывности выполняется тождественно, а функция давления принимает вид

Z

P = dp = p + const: %0 %0

Из уравнений остается уравнение движения и уравнение несжимаемости

1.4.1Задача об истечении жидкости из бочки.

В большой бочке налита жидкость. На глубине h от уровня жидкости в бочке имеется отверстие, через которое жидкость вытекает. Найти скорость истечения жидкости.

Начало координат расположим на уровне дна бочки и направим ось x3 z вертикально вверх. Массовая сила, приложенная к точкам жидкости везде одинакова, направлена вниз и по величине равна ускорению силы тяжести g

10

Рис. 1: Вытекание жидкости через отверстие в бочке

В процессе истечения уровень жидкости понижается следовательно течение, в принципе, неустановившееся. Однако если непрерывно доливать жидкость до уровня, то уровень не меняется и течение можно принять установившимся. В таком случае на линиях тока выполняется интеграл Бернулли.

Давление на поверхности жидкости везде одинаковое, а скорость точек жидкости на поверхности можно принять равной нулю.

Пусть линия тока начинается в какой либо точке A на поверхности и заканчивается в точке B на выходе из отверстия. Отверстие считаем малым так, что расстояние между линиями тока на выходе пренебрежимо мало. Интеграл Бернулли на этой линии во всех точках одинаков, следовательно

Рассмотрим водохранилище переполненное водой так, что она перетекает через плотину. Требуется найти скорость жидкости на поверхности воды после перелива.

Считаем водоём настолько большим, что вдали от плотины скорость поверхностных точек практически равна нулю. Течение является установившимся и поэтому на линиях тока справедлив интеграл Бернулли. Давление на поверхности жидкости везде равно атмосферному давлению.

Пусть точка А принадлежит поверхности водоёма вдали от плотины, а точка В лежит на поверхностной линии тока ниже уровня водоёма на величину h. Расположим начало декартовых координат на дне водоёма, а ось x3 z направим вертикально вверх.

11

Рис. 2: Схема перелива жидкости через плотину

Интеграл Бернулли принимает одинаковые значения в точках А и В, т.е.

1.4.3О сути подъёмной силы при обтекании различных профилей.

При обтекании крыла самолета воздушным потоком скорости v1 на стационарном участке полета движение воздуха является установившимся.

Рис. 3: Схема обтекания крыла

Рассмотрим несимметричное крыло (рис.3). Предполагаем, что контур сечения крыла является линией тока. Воздушная струя тормозится до нуля в точке C контура, при этом давление в этой точке будет максимальным. Далее струя раздваивается и в конце сечения вновь становится единой. Одна половинка материальной частицы движется по верхней части контуру, а вторая по нижней в направлении стрелок. Движение происходит так, что половинки частицы одновременно оказываются в точках А и В, расположенных на одной вертикали. Поскольку СВ > СА, постольку vB > v1 > vA < v1. Отсюда и из интеграла Бернулли

12

Отсюда следует, что pA > pB. Эта разность давлений и создаёт в итоге подъёмную силу, поддерживающую самолёт в полёте.

Такая ситуация конечно является идеализацией, точно также как и идеальная жидкость. Однако она помогает понять суть явления. Более подробно с теорией крыла можно познакомиться в специальной литературе, например в книге [3].

В случае обтекания симметричных профилей при нулевом угле атаки1 подъёмная сила, очевидно, равна нулю.

1.4.4Течение в трубе переменного сечения. Эффект пульверизатора.

При установившемся движении жидкости или газа в трубе переменного сечения предполагается, что вектор скорости жидкости перпендикулярен поперечному сечению и постоянен в каждом поперечном сечении, а величина скорости меняется от сечения к сечению (гипотеза плоских сечений), т.е. ~v = [v(x1); 0; 0).

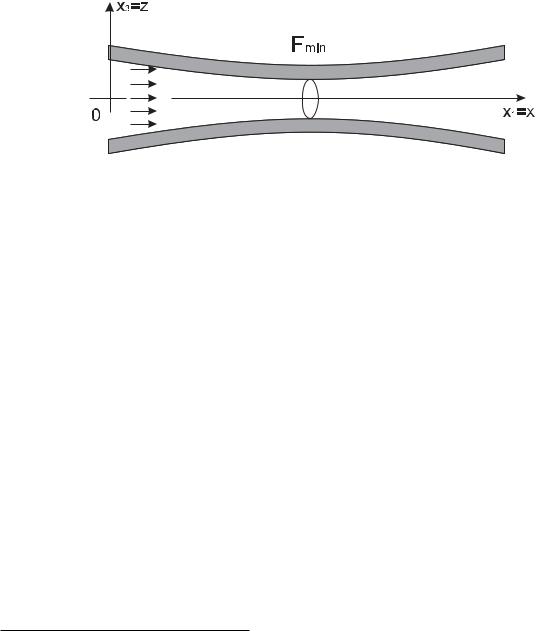
Рис. 4: Течение жидкости в трубе переменного сечения

Из закона сохранения массы следует, что объём несжимаемой жидкости, проходящий через каждое сечение в единицу времени будет величиной постоянной

Отсюда вытекает, что скорость будет максимальной в минимальном сечении.

При принятых предположениях течение будет безвихревым, т.е. 2!~ = rot ~v = 0. Следовательно интеграл Бернулли постоянен во всей области течения, причем при заданном значении z

В минимальном сечении трубы проделаем отверстие. Из последней формулы видно, что через это отверстие будет подсасываться содержимое внешней среды, когда внешняя среда находится под давлением p > pmin. На этом принципе построены пульверизатор, различные насосы, а также ряд других полезных устройств.

1.4.5Кавитация.

Из последней формулы (1.65) вытекает еще одно интересное следствие: при больших скоростях давление в жидкости в некоторых точках может становиться нулевым

1Угол атаки угол между осью профиля и направлением течения.

13