
1 курс / 1 курс 2 семестр / Теория_вероятностей_12_22_лекц_1К
.pdf
Теория вероятностей и математическая статистика
Лекция 12
1 курс. 4 зач.ед.
144 часа (36 час. лекц., 36 час. практич. зан., 72 час. самост. раб.). Экзамен.
1

Теория вероятностей и математическая статистика
11.4. Вероятность попадания в заданный интервал нормальной случайной величины
Известно, что если случайная величина X задана плотностью распределения f(x), то вероятность того, что X примет значение, принадлежащее интервалу ( , ), такова:
< < = |
( ). |
2
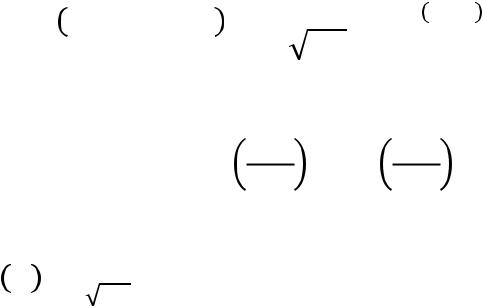
Теория вероятностей и математическая статистика
Ранее показано, что искомая вероятность
|
|
1 |
|
|
< < = |
|
− −a 2/(22) = |
||
|
2 |
|||
|
|
|||
|
|
|
= Ф −a − Ф −a , (*)
где Ф = |
|
|
|
− / – функция Лапласа, а новая |
|
|
|||
переменная z = (x-a)/ .
.
3
Теория вероятностей и математическая статистика
Пример. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что X примет значение, принадлежащее интервалу (10, 50).
4

Теория вероятностей и математическая статистика
Р е ш е н и е . Воспользуемся формулой
|
|
1 |
|
|
|
|
|
||
< < = |
|
|
− − 2/(2 2) = |
||||||
|
|
|
|
||||||
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
= Ф |
−a |
− Ф |
−a |
, |
|||||
|
|
|
|
||||||
|
|
|
|
||||||
По условию, = 10, |
|
= 50, а |
= 30, = 10 , |
||||||
следовательно, |
|
|
|
|
|
|
|
|
|
Р(10 < X < 50) = Ф(5010−30) - Ф(1010−30) = 2Ф(2)*.
*функция Лапласа – нечетная функция.
5

Теория вероятностей и математическая статистика
Р(10 < X < 50) = Ф(5010−30) - Ф(1010−30) = 2Ф(2).
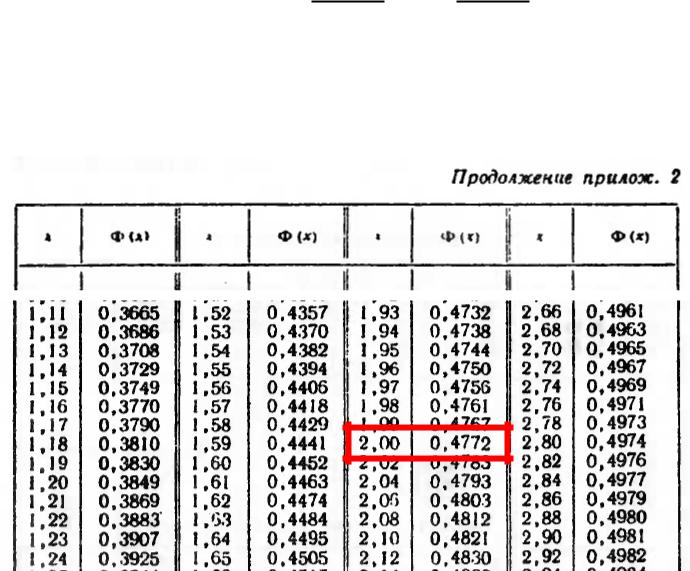
По таблице Приложения 2 находим Ф(2).
6
Теория вероятностей и математическая статистика
Р(10 < X < 50) = Ф(5010−30) - Ф(1010−30) = 2Ф(2).
Из таблицы приложения 2 следует: Ф(2) = 0,4772. Отсюда искомая вероятность
Р(10 < X < 50) = 2 0,4772 = 0,9544.
7
Теория вероятностей и математическая статистика
11.5. Вычисление вероятности заданного отклонения
Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины X по абсолютной величине меньше заданного положительного числа , т. е. требуется
найти вероятность осуществления неравенства
|Х-а|< .
Заменим это неравенство равносильным ему двойным неравенством
— < Х – а < , или а – < Х <а + .
8
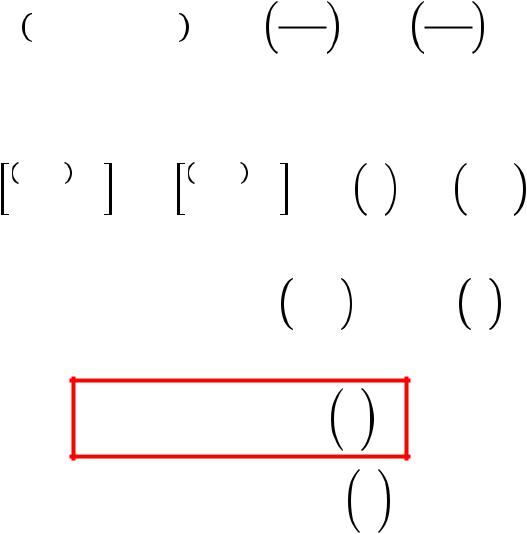
Теория вероятностей и математическая статистика
Пользуясь формулой
< < = Ф −a − Ф −a ,
получим
(| − a|< ) = ( − < < + ) =
=Ф |
a+ −a |
- Ф |
a− −a |
= Ф |
|
- Ф − |
|
. |
||
|
|
|
|
|
|
|||||
|
|
|
|
|
||||||
Приняв во внимание, что Ф − |
|
= - Ф |
|
(функция |
|
|
|
||||
|
|
|
|||
Лапласа нечетная), получим |
|
|
|
|
(|X-a|< )= Ф .
В частности, при а=0 (|X|< )= 2Ф |
. |
|
|
|
9 |

Теория вероятностей и математическая статистика
На рисунке показано, что если две случайные величины нормально распределены и а = 0, то вероятность
принять значение, принадлежащее интервалу (- , ), больше у той
величины, которая имеет меньшее значение .
Этот факт полностью соответствует вероятностному смыслу параметра ( есть среднее квадратическое
отклонение; оно характеризует рассеяние случайной величины вокруг ее математического ожидания).
10
