1 курс / 1 курс 2 семестр / Теория_вероятностей_11_22_лекц_1К

Теория вероятностей и математическая статистика

Лекция 11

1 курс. 4 зач.ед.

144 часа (36 час. лекц., 36 час. практич. зан., 72 час. самост. раб.). Экзамен.

1

Теория вероятностей и математическая статистика

10.2. Вероятность попадания непрерывной случайной величины в заданный интервал*

Зная плотность распределения, можно вычислить

вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу.

Это вычисление основано на следующей теореме.

*интервал – множество всех чисел, удовлетворяющих строгому неравенству a < x < b.

2

Теория вероятностей и математическая статистика

Теорема. Вероятность того, что непрерывная

распределения, взятому в пределах от а до b:

Р(а < Х < b) = .

3

Теория вероятностей и математическая статистика

Геометрически полученный результат можно истолковать так: вероятность того, что непрерывная

случайная величина примет значение, принадлежащее интервалу (а,b), равна площади криволинейной трапеции, ограниченной осью Ох, кривой распределения f(х) и прямыми х = а и х = b.

4

Теория вероятностей и математическая статистика

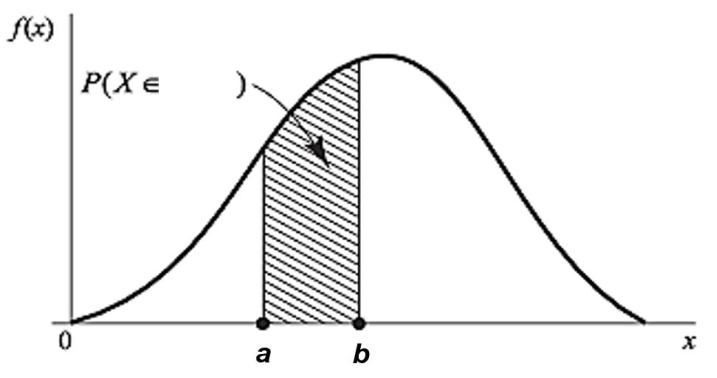
(a,b)

Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a,b), равна площади криволинейной трапеции, ограниченной осью Ох, кривой распределения f(х) и прямыми х = a и х = b.

5

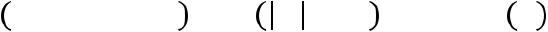
Теория вероятностей и математическая статистика

Замечание. В частности, если f(x) – четная функция и концы интервала симметричны относительно начала координат, то

− < < = < = 2 0 .

6

Теория вероятностей и математическая статистика

Пример. Задана плотность вероятности случайной величины X

0 при ≤ 0,

0 при > 1.

Найти вероятность того, что в результате испытания X примет значение, принадлежащее интервалу (0,5; 1).

Решение. Искомая вероятность

Р(0,5 < Х < 1) = 2 0,51 = 2|10,5 = 1 − 0,25 = 0,75

7

Теория вероятностей и математическая статистика

10.3. Нахождение функции распределения по известной плотности распределения

Зная плотность распределения f(x), можно найти функцию распределения F(х) по формуле

8

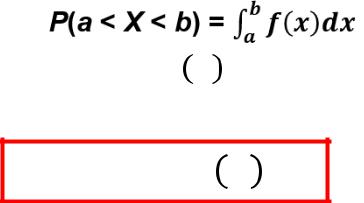
Теория вероятностей и математическая статистика

Действительно, мы обозначили через F(х) вероятность того, что случайная величина примет значение, меньшее x, т. е.

F(х) = Р(Х<х).

Очевидно, неравенство X<х можно записать в виде двойного неравенства — ∞< X < х, следовательно,

F(х) = Р(-∞<Х<х). (*)

) на F(x), в силу (*) окончательно получим

F(x)= −∞ .

9

Теория вероятностей и математическая статистика

Таким образом, зная плотность распределения, можно найти функцию распределения. Разумеется, по известной функции распределения может быть найдена плотность распределения.

10