
1 курс / 1 курс 2 семестр / Теория_вероятностей_11_22_лекц_1К
.pdf
Теория вероятностей и математическая статистика
График плотности равномерного распределения изображен на рисунке (а), а график функции равномерного распределения - на рисунке (b)
а)
b)
31
Теория вероятностей и математическая статистика
10.6. Числовые характеристики непрерывных случайных величин.
а) Математическое ожидание.
Пусть непрерывная случайная величина X задана плотностью распределения f(х). Допустим, что все возможные значения X принадлежат отрезку [а, b]. Разобьем этот отрезок на n частичных отрезков длиной
х1, х2, . . . . хn и выберем в каждом из них произвольную точку xi (i=1,2,…, n). Определим
математическое ожидание непрерывной величины по аналогии с дискретной.
32

Теория вероятностей и математическая статистика
Составим сумму произведений возможных значений xi на вероятности попадания их в интервал xi (вспомним, что
произведение f(х) x приближенно равно вероятности попадания X в интервал x):
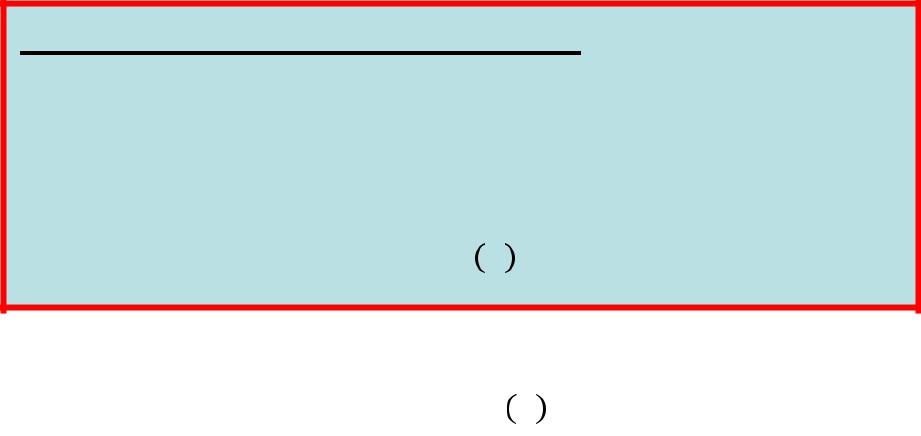
( ) .
Перейдя к пределу при стремлении к нулю длины наибольшего из частичных отрезков, получим определенный интеграл
.
|
33 |
Теория вероятностей и математическая статистика
Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называют определенный интеграл
M(X)= . (*)
Если возможные значения принадлежат всей оси Ох, то
M(X)= −∞∞ .
34
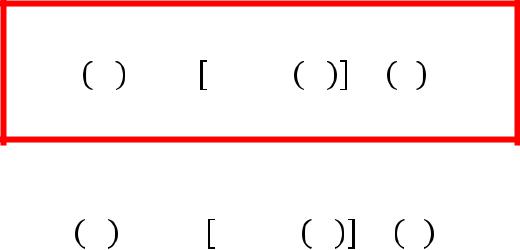
Теория вероятностей и математическая статистика
б) Дисперсия непрерывной случайной величины
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.
Если возможные значения X принадлежат отрезку [a, b], то
= − 2 .
Если возможные значения принадлежат всей оси х, то
|
∞ |
|
= |
− |
2 . |
|
−∞ |
35 |
|
|

Теория вероятностей и математическая статистика
в) Среднее квадратическое отклонение непрерывной случайной величины
Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством
= .
36

Теория вероятностей и математическая статистика
Замечание 1.
Свойства математического ожидания и дисперсии дискретных величин сохраняются и для непрерывных величин.
37

Теория вероятностей и математическая статистика
Замечание 2. Легко получить для вычисления дисперсии более удобные формулы:
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
− |
|
|
, |
|
|
|
|
|
|
|
|
(**) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
− |
|
|
|
|
||
|
− |
|
|
. |
|
||||||
38
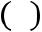
Теория вероятностей и математическая статистика
Пример 1. Найти математическое ожидание и дисперсию случайной величины X, заданной функцией распределения
|
0 при ≤ 0, |
= |
при 0 < ≤ 1, |
|
1 при > 1, |
39

Теория вероятностей и математическая статистика
Решение. Найдем плотность распределения
|
0 при ≤ 0, |
( ) = ′ = |
1 при 0 < ≤ 1, |
0 при > 1.
Найдем математическое ожидание по формуле (*):
( ) = 01 1 = 2/2|10=1/2
Найдем дисперсию по формуле (**):
= |
1 2 1 dx – [1/2]2 = x3/3|1 |
- 1/4 = 1/12. |
|
|
0 |
0 |
|
|
|
|
|
40
